Dean sayısı

Dean sayısı (De), akışkanlar mekaniği alanında, özellikle eğri borular ve kanallarda meydana gelen akış dinamiklerinin incelenmesinde kullanılan bir boyutsuz sayıdır. Bu terim, Britanyalı bilim insanı William Reginald Dean'in adını taşımaktadır. Dean, laminer akış durumunda, düz bir borudaki Poiseuille akışından, çok küçük bir eğrilik içeren bir boruya kadar olan akışın teorik çözümünü bir bozulma yöntemi kullanarak ilk kez sunmuştur. Bu çalışma, eğri borulardaki akış mekaniklerinin anlaşılmasında temel bir adım olarak kabul edilir.^[1][2]

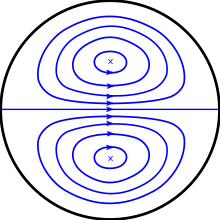
Eğer bir sıvı, başlangıçta düz olan ancak belirli bir noktadan itibaren eğim kazanan bir boru içerisinde akıyorsa, eğim noktasındaki merkezkaç kuvvetleri sıvı partiküllerinin ana hareket yönünde değişiklik yaratır.^[3] Eğrilik nedeniyle oluşan advers basınç gradyanı, basıncın artmasına ve dolayısıyla borunun konveks duvarına yakın kısımlarda sıvı hızının azalmasına yol açar; borunun dış kısmında ise tam tersi bir etki gözlemlenir. Bu durum, primer akış üzerine eklenmiş ikincil bir hareketi tetikler; borunun merkezi kısmındaki sıvı, eğimin dış kısmına doğru itilirken, boru duvarına yakın sıvı ise eğimin iç kısmına doğru geri yönelir. Bu ikincil hareket, genellikle birbirine zıt yönde dönen çift hücre şeklinde ortaya çıkar ve bu yapılar Dean girdapları olarak adlandırılır. Bu girdaplar, borunun eğimli kısımlarında sıvı akış dinamiklerinin karmaşık bir özelliğini temsil eder ve akışkan mekaniğinde önemli bir fenomen olarak kabul edilir.

Dean sayısı, akışkanlar mekaniği alanında, genellikle De (veya Dn) simgesi ile ifade edilir. Boru veya tüp içerisindeki bir akış için şu şekilde formüle edilmiştir:

${\displaystyle {\mathit {De}}={\frac {\sqrt {{\frac {1}{2}}({\text{eylemsiz kuvvetler}})({\text{merkezkaç kuvvetleri}})}}{\text{viskoz kuvvetler}}}={\frac {\sqrt {{\frac {1}{2}}\,(\rho \,D^{2}\,R_{c}\,{\frac {v^{2}}{D}})(\rho \,D^{2}\,R_{c}\,{\frac {v^{2}}{R_{c}}})}}{\mu {\frac {v}{D}}D\,R_{c}}}={\frac {\rho \,D\,v}{\mu }}{\sqrt {\frac {D}{2\,R_{c}}}}={\textit {Re}}\,{\sqrt {\frac {D}{2\,R_{c}}}}}$

Bu formülasyonda;

• ${\displaystyle \rho }$, akışkanın yoğunluğunu,
• ${\displaystyle \mu }$, dinamik viskoziteyi,
• ${\displaystyle v}$, eksensel sürat ölçeğini,
• ${\displaystyle D}$, borunun veya kanalın çapını (dairesel olmayan geometriler için kullanılan eşdeğer çapı içerir; bkz. Reynolds sayısı),
• ${\displaystyle R_{c}}$, kanalın izlediği yolun eğrilik yarıçapını,
• ${\displaystyle {\textit {Re}}}$, Reynolds sayısını belirtir.

Dean sayısı, boru çapı ${\displaystyle D}$ üzerinden hesaplanan eksenel akış sürati ${\displaystyle v}$ baz alınan Reynolds sayısının ve eğrilik oranının karekökünün çarpımı olarak ifade edilir.

Düşük Dean sayıları (De < 40~60) için akış tamamen tek yönlüdür. Dean sayısı 40~60 ile 64~75 arasında yükseldiğinde, kesitlerde dalgalı bozulmalar gözlemlenebilir ki bu, ikincil akışların varlığını gösterir. Dean sayısı 64~75'in üzerine çıktığında, Dean girdaplarının çifti stabil bir yapıya kavuşur, bu da birincil dinamik istikrarsızlığın bir göstergesidir. Dean sayısı 75~200'ü geçtiğinde, girdaplı dalgalanmalar, bükülmeler sergileyebilir ve nihayetinde birleşerek çift bölünmeye yol açabilir. Dean sayısı 400'ü aştığında ise tamamen türbülanslı bir akış ortaya çıkar.^[4] Laminerden türbülanslı akışa geçiş süreci, birçok araştırmada değerlendirilmiş olup, bu parametre yüksek derecede eğrilik oranına bağımlı olduğundan evrensel bir çözüm önerilmemektedir.^[5] Beklenmedik bir biçimde, eğriliğin bilinen istikrarsızlık yaratıcı etkisine rağmen, laminer akış düz borularda elde edilenden (çalışılan en yüksek eğrilik oranlarında iki katına kadar) daha büyük Reynolds sayıları için muhafaza edilebilir.^[6]

Dean sayısı, 'Dean denklemleri' adı verilen yaklaşık formüllerde yer almaktadır.^[7] Bu denklemler, bir toroidal boru içerisindeki Newton tipi akışkanın sabit eksenel uniform akışı için Navier–Stokes denklemlerinin tamamına bir yaklaşım olarak geliştirilmiştir ve sadece ilk mertebe eğrilik etkilerini içerecek şekilde (${\displaystyle a/r\ll 1}$ için) formüle edilmiştir. Bu, özellikle toroidal borularda sıvı dinamiklerinin anlaşılması için kritik öneme sahiptir.

Bu denklemlerde, ortogonal koordinatlar ${\displaystyle (x,y,z)}$ kullanıldığı varsayılırsa, ilgili birim vektörler ${\displaystyle ({\hat {\boldsymbol {x}}},{\hat {\boldsymbol {y}}},{\hat {\boldsymbol {z}}})}$ borunun merkez çizgisi ile hizalanmış şekilde her noktada tanımlanır. Eksenel yön, ${\displaystyle {\hat {\boldsymbol {z}}}}$, ${\displaystyle {\hat {\boldsymbol {x}}}}$ merkez çizgisinin düzlemine normal, ${\displaystyle {\hat {\boldsymbol {y}}}}$ ise binormaldir. Basınç gradyanı ${\displaystyle G}$ tarafından sürüklenen eksenel akışın sürati ${\displaystyle u_{z}}$, ${\displaystyle U=Ga^{2}/\mu }$ ile ölçeklenirken, çapraz akış süratleri ${\displaystyle u_{x},u_{y}}$ ${\displaystyle (a/R)^{1/2}U}$ ile ve çapraz akış basınçları ${\displaystyle \rho aU^{2}/L}$ ile ölçeklenir. Uzunluklar, borunun yarıçapı ${\displaystyle a}$ ile ölçeklenir.

Bu boyutsuz değişkenler ve koordinatlar çerçevesinde, Dean denklemleri şöyle formüle edilmiştir:

${\displaystyle De\left({\frac {\mathrm {D} u_{x}}{\mathrm {D} t}}-u_{z}^{2}\right)=-De{\frac {\partial p}{\partial x}}+\nabla ^{2}u_{x}}$

${\displaystyle De{\frac {\mathrm {D} u_{y}}{\mathrm {D} t}}=-De{\frac {\partial p}{\partial y}}+\nabla ^{2}u_{y}}$

${\displaystyle De{\frac {\mathrm {D} u_{z}}{\mathrm {D} t}}=1+\nabla ^{2}u_{z}}$

${\displaystyle {\frac {\partial u_{x}}{\partial x}}+{\frac {\partial u_{y}}{\partial y}}=0}$

Burada,

${\displaystyle {\frac {\mathrm {D} }{\mathrm {D} t}}=u_{x}{\frac {\partial }{\partial x}}+u_{y}{\frac {\partial }{\partial y}}}$

ifadesi taşınım türevi olarak adlandırılır ve akışkan mekaniğindeki temel hareket denklemlerinin boyutsuzlaştırılmış formülasyonunu temsil eder.

Dean sayısı De, sistemdeki tek değişken olarak kalmıştır ve eğrilik etkilerinin ilk mertebe dinamiklerini içermektedir. İleri mertebeli yaklaşımlar ek parametreler gerektirecektir.

Zayıf eğrilik etkilerinin olduğu durumlarda (küçük De), Dean denklemleri De terimleriyle seri genişlemesi şeklinde çözümlenebilir. Eksenel Poiseuille akışının ilk mertebe çözümüne yapılan ilk düzeltme, akışın virajın iç kısmından dış kısmına doğru ve tekrar kenarlar üzerinden merkeze geri dönmesini sağlayan bir çift girdap şeklinde olur. Bu çözüm, yaklaşık ${\displaystyle De_{c}\approx 956}$ değerinde bir kritik Dean sayısına kadar stabil kalır.^[8]

De değeri büyüdükçe, sistem çok sayıda çözüm sunar ve bu çözümlerin çoğu istikrarsızdır. Bu durum, akışkanlar mekaniğinde eğri geometrilerin analizinde karşılaşılan temel bir zorluk olarak kabul edilir ve çeşitli akış rejimlerinin stabilitesini değerlendirmede önemli bir rol oynar.

• Berger, S. A.; Talbot, L.; Yao, L. S. (1983). "Flow in Curved Pipes". Annu. Rev. Fluid Mech. Cilt 15. ss. 461-512. Bibcode:1983AnRFM..15..461B. doi:10.1146/annurev.fl.15.010183.002333.