Laplasyen 
, skaler bir 
alanının gradyanı alınarak elde edilen vektörün diverjansıdır. Fizikteki birçok diferansiyel denklem laplasyen içerir.
Gök mekaniğinde yörünge veya yörünge hareketi, bir gezegenin yıldız etrafındaki veya bir doğal uydunun gezegen etrafındaki veya bir gezegen, doğal uydu, asteroit veya lagrange noktası gibi uzaydaki bir nesne veya konum etrafındaki yapay uydunun izlediği kavisli bir yoldur. Yörünge, düzenli olarak tekrar eden bir yolu tanımlamakla birlikte, tekrar etmeyen bir yolu da ifade edebilir. Gezegenler ve uydular Kepler'in gezegensel hareket yasalarında tanımlandığı gibi, kütle merkezi elips biçiminde izledikleri yolun odak noktasında olacak şekilde yaklaşık olarak eliptik yörüngeleri takip ederler.
Navier-Stokes denklemleri, ismini Claude-Louis Navier ve George Gabriel Stokes'tan almış olan, sıvılar ve gazlar gibi akışkanların hareketini tanımlamaya yarayan bir dizi denklemden oluşmaktadır.
Matematikte kutupsal koordinat sistemi veya polar koordinat sistemi, noktaların birer açı ve Kartezyen koordinat sistemindeki orijinin eşdeğeri olup "kutup" olarak bilinen bir merkez noktaya olan uzaklıklar ile tanımlandığı, iki boyutlu bir koordinat sistemidir. Kutupsal koordinat sistemi, matematik, fizik, mühendislik, denizcilik, robot teknolojisi gibi birçok alanda kullanılır. Bu sistem, iki nokta arasındaki ilişkinin açı ve uzaklık ile daha kolay ifade edilebildiği durumlar için özellikle kullanışlıdır. Kartezyen koordinat sisteminde, böyle bir ilişki ancak trigonometrik formüller ile bulunabilir. Kutupsal denklemler, çoğu eğri tipi için en kolay, bazıları içinse yegâne tanımlama yöntemidir.
Yarıçap, bir daire veya kürenin özeğinin (merkezinin) çemberine olan mesafesidir. Çapın yarısına eşittir.
Akışkanlar dinamiği alanında, Reynolds sayısı, farklı durumlarda akışkan akışı desenlerini tahmin etmeye yardımcı olan bir boyutsuz sayıdır ve eylemsizlik kuvvetleri ile viskoz kuvvetler arasındaki oranı ölçer. Düşük Reynolds sayılarında, akışlar genellikle laminer akış tarafından domine edilirken, yüksek Reynolds sayılarında akışlar genellikle türbülanslı olur. Türbülans, akışkanın hız ve yönündeki farklılıklardan kaynaklanır ve bazen bu yönler kesişebilir veya akışın genel yönüne ters hareket edebilir. Bu girdap akımları, akışı karıştırmaya başlar ve bu süreçte enerji tüketir, bu da sıvılarda kavitasyon olasılığını artırır.
Jean Léonard Marie Poiseuille, Fransız Tıp doktoru, matematikçi ve fizyolog.
Akım Fonksiyonu, eksen simetrisi ile üç boyutta olduğu kadar iki boyutta sıkıştırılamaz akışlar için tanımlanır. Akış hızı bileşenleri, skaler akış fonksiyonunun türevleri olarak ifade edilebilir. Akım fonksiyonu, kararlı akıştaki partiküllerin yörüngelerini gösteren akım çizgileri, çıkış çizgileri ve yörüngeyi çizmek için kullanılabilir. İki boyutlu Lagrange akım fonksiyonu, 1781'de Joseph Louis Lagrange tarafından tanıtıldı. Stokes akım fonksiyonu, eksenel simetrik üç boyutlu akış içindir ve adını George Gabriel Stokes'tan almıştır.
Dean akışı, eğrisel kanallarda eğrilikten kaynaklanan bir akıştır. Dean akışı, Dean sayısının büyümesi ile etkisini gösterir. Dean sayısı boyutsuz bir sayıdır. İngiliz araştırmacı William Reginald Dean kanal içindeki akış için Dean sayısını:
Dean sayısı (De), akışkanlar mekaniği alanında, özellikle eğri borular ve kanallarda meydana gelen akış dinamiklerinin incelenmesinde kullanılan bir boyutsuz sayıdır. Bu terim, Britanyalı bilim insanı William Reginald Dean'in adını taşımaktadır. Dean, laminer akış durumunda, düz bir borudaki Poiseuille akışından, çok küçük bir eğrilik içeren bir boruya kadar olan akışın teorik çözümünü bir bozulma yöntemi kullanarak ilk kez sunmuştur. Bu çalışma, eğri borulardaki akış mekaniklerinin anlaşılmasında temel bir adım olarak kabul edilir.
Kerr–Newman metriği genel relativitide yüklü, dönen kütlelerin çevresindeki uzay zaman geometrisini tarif eden Einstein–Maxwell denklemlerinin çözümüdür. Bu çözüm astrofizik alanındaki fenomenler için pek faydalı sayılmaz çünkü gözlemlenebilen astronomik objeler kayda değer net yük taşımazlar. Bu çözüm uygulama alanı yerine daha çok teorik fizik ve matematiksel ilginin bir sonucudur..
Gök mekaniği olarak, Kepler yörüngesi üç boyutlu uzayda iki boyutlu bir yörünge düzlemi oluşturan bir elips, parabol, hiperbol benzeri bir yörünge cismininin hareketini açıklar.. Kepler yörüngesi yalnızca nokta iki cismin nokta benzeri yerçekimsel çekimlerini dikkate alır, atmosfer sürüklemesi, güneş radyasyonu baskısı, dairesel olmayan cisim merkezi ve bunun gibi bir takım şeylerin diğer cisimlerle girdiği çekim ilişkileri nedeniyle ihmal eder. Böylece Kepler problemi olarak bilinen iki-cisim probleminin, özel durumlara bir çözüm olarak atfedilir. Klasik mekaniğin bir teorisi olarak, aynı zamanda genel görelilik etkilerini dikkate almaz. Kepler yörüngeleri çeşitli şekillerde altı yörünge unsurları içine parametrize edilebilir.
Dikey eksenli rüzgar türbini (DERT), ana rotor milinin rüzgara enine yerleştirildiği ve ana bileşenlerin türbinin tabanında yer aldığı bir rüzgar türbin türüdür. Bu düzenleme, jeneratör ve dişli kutusunun yere yakın yerleştirilmesine olanak tanıyarak servis ve onarımı kolaylaştırır. DERT'lerin rüzgara doğrultulmasına gerek yoktur, bu ise rüzgar algılama ve yönlendirme mekanizmalarına olan ihtiyacı ortadan kaldırır. İlk tasarımların başlıca dezavantajları arasında her devir sırasında önemli tork dalgalanması ve kanatlar üzerindeki büyük bükülme momentleri vardı. Daha sonraki tasarımlar, kanatları sarmal olarak süpürerek tork dalgalanmasını giderdi.
Akışkanlar mekaniğinde, Helmholtz teoremleri, girdap (vorteks) filamanlarının çevresindeki üç boyutlu akışkan hareketlerini tanımlar. İsmini Hermann von Helmholtz'den alan bu teoremler, viskoz olmayan akışlarda ve viskozite etkisinin az olup göz ardı edilebileceği akışlarda geçerlidir.
Hartmann sayısı (Ha), ilk olarak Danimarkalı Julius Hartmann tarafından tanıtılan, elektromanyetik kuvvetin viskoz kuvvete oranıdır. Sıklıkla manyetik alanlar içindeki akışkan akışlarında karşılaşılır. Şu şekilde tanımlanır:
Akışkanlar mekaniğinde, Rayleigh sayısı (Ra, Lord Rayleigh'e ithafen) bir akışkan için kaldırma kuvveti ilişkili bir boyutsuz sayıdır. Bu sayı, akışkanın akış rejimini karakterize eder: belirli bir alt aralıkta bir değer laminer akışı belirtirken, daha yüksek bir aralıktaki değer türbülanslı akışı belirtir. Belirli bir kritik değerin altında, akışkan hareketi olmaz ve ısı transferi konveksiyon yerine ısı iletimi ile gerçekleşir. Çoğu mühendislik uygulaması için Rayleigh sayısı büyük olup, yaklaşık 106 ile 108 arasında bir değerdedir.
Richardson sayısı (Ri), Lewis Fry Richardson (1881–1953) adını taşıyan boyansi teriminin akış kayma gerilmesi terimine oranını ifade eden bir boyutsuz sayı:
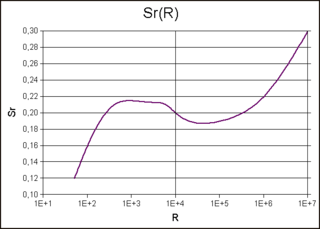
Boyut analizinde, Strouhal sayısı salınımlı akış mekanizmalarını tanımlayan bir boyutsuz sayıdır. Bu parametre, 1878 yılında vorteks saçıntısı oluşturan tellerle ve rüzgarda ses çıkaran tellerle deney yapan Çek fizikçi Vincenc Strouhal'ın adını taşır. Strouhal sayısı, akışkanlar mekaniğinin temel ilkelerinin önemli bir bileşenidir.
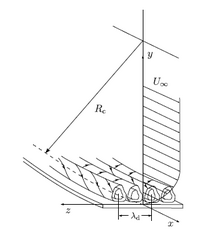
Akışkanlar dinamiğinde, Taylor sayısı (Ta), bir akışkanın bir eksen etrafında dönmesine bağlı olarak ortaya çıkan merkezkaç "kuvvetlerin" veya sözde atalet kuvvetlerinin viskoz kuvvetlere göre önemini karakterize eden bir boyutsuz niceliktir.
. Annual Review of Fluid Mechanics. Cilt 28. ss. 477-539. Bibcode:1996AnRFM..28..477W. doi:10.1146/annurev.fl.28.010196.002401. 16 Haziran 2022 tarihinde kaynağından arşivlendi. Erişim tarihi: 25 Mayıs 2024.
