
Bir üçgen düzlemde birbirine doğrusal olmayan üç noktayı birleştiren üç doğru parçasının birleşimidir. Üçgene müselles ve üçbucak da denir.
Altın oran, matematikte iki miktardan büyük olanın küçüğe oranı, miktarların toplamının miktarları büyük olanına oranı ile aynı ise altın orandır. Altın oran aynı zamanda antik çağdan bu yana sanat ve mimaride en iyi uyum ve oranları veren düzen bağıntısı olarak kabul edilmekteydi.

Kare, murabba veya dördül, bütün kenarları ve açıları birbirine eşit olan düzgün dörtgendir. Matematiğin en temel geometrik şekillerinden biridir. Bir kare aynı zamanda dikdörtgen ve eşkenar dörtgendir. Bu iki özel dörtgenin tüm özelliklerini taşır. Eski adı ise murabbadır.
Alan veya yüz ölçümü, bir yüzeyin uzayda kapladığı iki boyutlu yer miktarını ölçen bir büyüklüktür. SI birim sisteminde temel alan birimi metrekaredir (m²). Diğer alan birimleri bundan türetilebilir:
- Ar = 100 metrekare (m²)
- Dekar = 1000 metrekareye (m²)
- Hektar = 10.000 metrekare (m²)
- Kilometrekare = 1.000.000 metrekare (m²)

Çember ya da dönge, düzlemde sabit bir noktaya eşit uzaklıkta bulunan noktaların kümesinin oluşturduğu yuvarlak, geometrik şekil. Çemberin çevrelediği 2 boyutlu alana daire denir.

Koni, matematikte, bir düzlem içindeki dairenin her noktasını, düzlem dışındaki bir noktaya birleştiren doğru parçalarının meydana getirdiği geometrik şekil.

Yarıçap, bir daire veya kürenin özeğinin (merkezinin) çemberine olan mesafesidir. Çapın yarısına eşittir.

Dikdörtgen, karşılıklı kenarları birbirine eşit, dik ve paralel olan dörtgene denir.

Paralelkenar, karşılıklı kenarları eşit olan ve iç açıları toplamı 360 derece olan bir dörtgendir. Karşılıklı kenarları paralel ve uzunlukları eşittir.

Matematiğin bir alt dalı olan Geometride bir eşkenar dörtgen, dört kenarlı ve tüm kenar uzunlukları birbirine eşit bir dörtgendir. Oyun kâğıtlarında görülen eşkenar dörtgene karo, bu şekle sahip olan haplara lozanj, bu şekle sahip olan beyzbol oyun sahasına diamond (elmas) denir.
Sıkışabilir akışkan bir ortamda yol alan herhangi bir araç ya da gövde ye ait burun konisi kısmının aerodinamik tasarımındaki, önemli bir problem burun konisinin geometrik şeklinin belirlenmesidir. Burun konisinin şekli optimum performans için gereklidir. Dönel katı cisim şekil tanımlamasının gerektiği işler gibi birçok uygulamalar, akışkan bir ortamda çok hızlı hareket eden böyle bir cismin karşılaşacağı direncin en aza indirilmesini gerektirir.

Yamuk, iki kenarı paralel olan dörtgen. Paralel olan kenarlarına "yamuğun tabanları", paralel olmayan kenarlarına ise "yanal kenarlar" adı verilir.
Prizma ya da biçme, genelde en boy ve yükseklik kavramlarına sahip cisimler olarak adlandırılır. Ancak bazı cisimlerin (küre) en ve boyu tam olarak ifade edilememekle çap ve çevre de bu nicelikleri belirtmek için kullanılır.
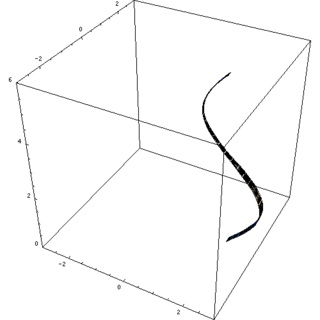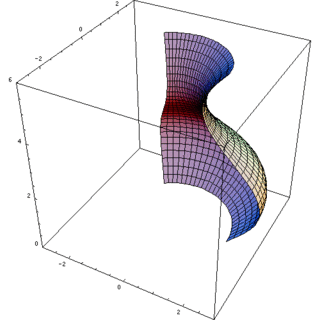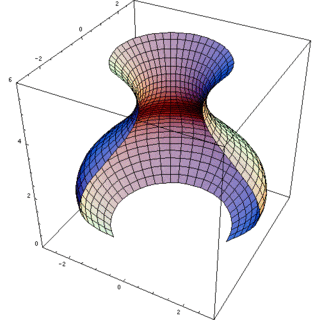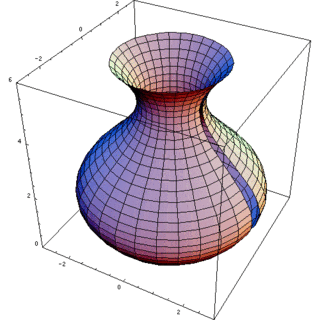
Matematik, mühendislik ve imalat alanlarında kullanılan dönel cisim, bir eğriyi aynı düzlemde bulunan bir doğru etrafında döndürülerek elde edilen şekildir.

Geometride, Theodorus Sarmalı, uç uca yerleştirilmiş dik üçgenlerden oluşan bir spiraldir. Adını, Cyreneli Theodorus'tan almıştır.

Gnomon teoremi, bir gnomon'da meydana gelen belirli paralelkenarların eşit büyüklükte alanlara sahip olduğunu belirtir. Gnomon, geometride benzer bir paralelkenarı daha büyük bir paralelkenarın bir köşesinden çıkararak oluşturulan bir düzlem şeklidir; veya daha genel olarak, belirli bir şekle eklendiğinde, aynı şekle sahip daha büyük bir şekil oluşturan bir şekildir.
Geometride, bir çokgenin yarı çevresi, çevre uzunluğunun yarısıdır. Çevreden doğrudan türetilebilmesine rağmen, yarı çevre üçgenler ve diğer şekiller için kullanılan formüllerde oldukça sık görülür ve ayrı/özel bir isim verilir. Yarı çevre, bir formülün parçası olarak ortaya çıktığında, genellikle s harfiyle gösterilir.
















