
Geometride büyük eksen, bir elipsin en uzun çapıdır. Merkezden ve her iki odak noktasından geçen ve çevre uzunluğunun (perimetre) en uzak noktalarında sonlanan bir doğru parçasıdır. Yarı büyük eksen, en uzun yarıçap veya büyük eksenin yarısıdır ve bu nedenle merkezden bir odağa ve çevreye doğru uzanır. Bir elips veya hiperbolün yarı küçük ekseni, yarı büyük eksenle dik açı yapan ve bir ucu konik kesitin merkezinde olan bir doğru parçasıdır. Bir dairenin özel durumu için yarı eksen uzunluklarının her ikisi de dairenin yarıçapına eşittir.

Analitik geometri, geometrik çalışmaya cebrik analizi uygulayan ve cebrik problemlerin çözümünde geometrik kavramları kullanan bir matematik dalı. Bütün bunlar kartezyen sistem denilen bir koordinat sisteminin kullanılmasıyla mümkündür. Kartezyen kelimesi, batıda analitik geometride ilk bilimsel çalışmayı yapan René Descartes'tan gelmektedir.

Pergeli Apollonius, konik kesitler üzerindeki çalışmaları ile tanınan Antik Yunan geometri uzmanı ve astronom. Öklid ve Arşimet'in konuya katkılarından başlayarak, onları analitik geometrinin icadından önceki duruma getirdi. Elips, parabol ve hiperbol terimlerinin tanımları bugün kullanımda olanlardır.

Konik kesit, eliptik veya dairesel bir çift taraflı koninin, düzlemle kesitinden meydana gelen eğriler. Bunlar, çember, elips, parabol ve hiperboldür.

Matematikte kutupsal koordinat sistemi veya polar koordinat sistemi, noktaların birer açı ve Kartezyen koordinat sistemindeki orijinin eşdeğeri olup "kutup" olarak bilinen bir merkez noktaya olan uzaklıklar ile tanımlandığı, iki boyutlu bir koordinat sistemidir. Kutupsal koordinat sistemi, matematik, fizik, mühendislik, denizcilik, robot teknolojisi gibi birçok alanda kullanılır. Bu sistem, iki nokta arasındaki ilişkinin açı ve uzaklık ile daha kolay ifade edilebildiği durumlar için özellikle kullanışlıdır. Kartezyen koordinat sisteminde, böyle bir ilişki ancak trigonometrik formüller ile bulunabilir. Kutupsal denklemler, çoğu eğri tipi için en kolay, bazıları içinse yegâne tanımlama yöntemidir.

Başlangıçta sonsuz küçük hesap veya "sonsuz küçüklerin hesabı" olarak adlandırılan kalkülüs, geometrinin şekillerle çalışması ve cebirin aritmetik işlemlerin genellemelerinin incelenmesi gibi, kalkülüs sürekli değişimin matematiksel çalışmasıdır.

Yarıçap, bir daire veya kürenin özeğinin (merkezinin) çemberine olan mesafesidir. Çapın yarısına eşittir.

Geometri'de iki çeşit eğrilik tanımlanır. Eğrilik ve özeğrilik. Tarihte ilk olarak 2-boyutlu ve 3-boyutlu uzayda parametrik eğrilerin eğriliği incelendi. Daha sonraki aşamada 2-boyutlu ve 3-boyutlu yüzeylerin eğriliği incelendi ve ortalama eğrilik, Gaussian eğrilik gibi kavramlar ortaya çıktı.
Çukur ayna üzerine gelen ışınları belli bir noktada toplayan ayna.

Apsis, gök mekaniğinde, eliptik yörüngedeki bir cismin genelde sistemin kütle merkezi durumunda da olan çekim merkezine yörünge boyunca en yakın ve en uzak olduğu noktalara verilen addır.
Matematikte, bir kuvvet serisinin yakınsaklık yarıçapı negatif olmayan bir gerçel sayı veya ∞ olan bir niceliktir. Verilen bir kuvvet serisinin yakınsaklık yarıçapı serinin yakınsak olduğu bölgeyi gösterir. Bu yakınsaklık yarıçapının içinde kalan bölgede, kuvvet serisi mutlak yakınsak ve aynı zamanda tıkız yakınsaktır. Seri yakınsak ise, o zaman bu seri bir analitik fonksiyonun bu yakınsaklık yarıçapının belirlediği bölgenin içinde kalan bölgede yakınsayan bir Taylor serisidir.

Matematikte bir doğrunun eğimi ya da gradyanı o doğrunun dikliğini, eğimliliğini belirtir. Daha büyük eğim, daha dik bir doğru demektir.

Mercek ya da lens ışığın yönünü değiştiren (kıran), ışık ışınlarını birbirine yaklaştıran ya da uzaklaştıran optik alet.
Basit mercek tek bir optik elemanın kullanıldığı, bileşik mercek ise iki optik elemanın bir arada olduğu mercek tipidir. Bileşik mercek, basit mercek kullanıldığında ortaya çıkan sapınç olayının etkisini azaltmak için kullanılır. Mercekler genelde camdan ve saydam plastikten yapılır. Lensler, gereken şekle göre taşlanır, parlatılır veya kalıplanır. Bir mercek, ışığı odaklamadan kıran bir prizmadan farklı olarak, bir görüntü oluşturmak için ışığı odaklayabilir. Mikrodalga lensler, elektron lensler, akustik lensler veya patlayıcı lensler gibi görünür ışık dışındaki dalgaları ve radyasyonu benzer şekilde odaklayan veya dağıtan cihazlara da "mercekler" denir.
Matematikte bir fonksiyonun limiti, kalkülüs ve analizde kullanılan bir temel kavramdır ve belirli bir girişe yaklaşan bir fonksiyonun davranışı ile ilgilidir.

Düzgün olmayan rasyonel temelli eğri, eğrileri ve yüzeyleri oluşturmak ve temsil etmek için bilgisayar grafiklerinde yaygın olarak kullanılan matematiksel bir modeldir. Hem analitik hem de modellenmiş şekilleri işlemek için büyük esneklik ve hassasiyet sunar. NURBS yaygın olarak bilgisayar destekli tasarım, imalat ve mühendislikte kullanılır ve IGES, STEP, ACIS ve PHIGS gibi çok sayıda endüstri çapında standardın parçasıdır. NURBS araçları ayrıca çeşitli 3B modelleme ve animasyon yazılım paketlerinde de bulunur. NURBS yüzeyleri, üç boyutlu uzayda bir yüzeye eşlenen iki parametrenin işlevleridir. Yüzeyin şekli kontrol noktaları ile belirlenir. NURBS yüzeyleri, kompakt bir biçimde basit geometrik şekilleri temsil edebilir. T-spline'lar ve alt bölme yüzeyleri, NURBS yüzeylerine kıyasla kontrol noktalarının sayısını iki kat azalttığı için karmaşık organik şekiller için daha uygundur. NURBS eğrilerini ve yüzeylerini düzenlemek oldukça sezgisel ve öngörülebilirdir. Kontrol noktaları her zaman doğrudan eğriye / yüzeye bağlanır veya bir lastik bantla bağlanmış gibi davranır. Kullanıcı arayüzünün türüne bağlı olarak, düzenleme, Bézier eğrileri için en açık ve yaygın olan bir elemanın kontrol noktaları aracılığıyla veya spline modelleme veya hiyerarşik düzenleme gibi daha yüksek seviyeli araçlar aracılığıyla gerçekleştirilebilir.

Bézout teoremi, cebirsel geometride n değişkenli n polinomun ortak sıfırlarının sayısı ile ilgili bir ifadedir. Orijinal biçiminde teorem, genel olarak ortak sıfırların sayısının, polinomların derecelerinin çarpımına eşit olduğunu belirtir. Adını Fransız matematikçi Étienne Bézout'dan almıştır.

Eğrilik yarıçapı optik tasarımda özel bir anlam ve işaret kuralına sahiptir. Küresel bir mercek veya ayna yüzeyi, sistem yerel optik ekseni boyunca veya merkezden uzakta bulunan bir eğrilik merkezine sahiptir. Mercek yüzeyinin tepe noktası, yerel optik eksende bulunur. Mercek tepe noktasından eğrilik merkezine olan mesafe, yüzeyin eğrilik yarıçapıdır.
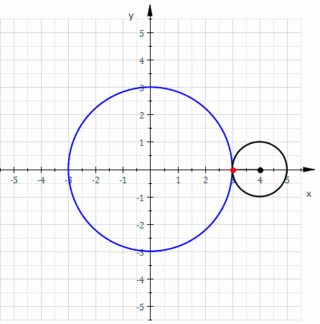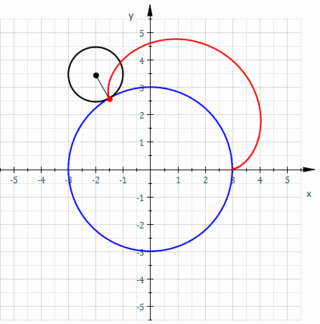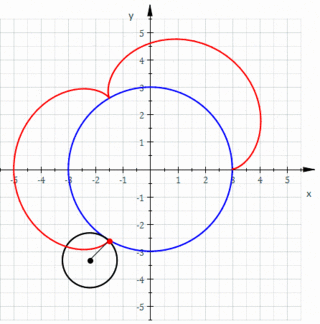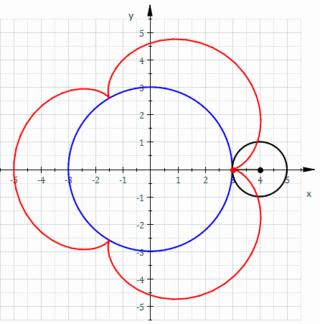
Geometride, bir episikloid, sabit bir çemberin etrafında kaymadan yuvarlanan bir çemberin çevresi üzerinde seçilen bir noktanın yolunu izleyerek üretilen bir düzlem eğrisidir -buna episikl (epicycle) denir. Bu, yuvarlanma eğrisinin özel bir türüdür.
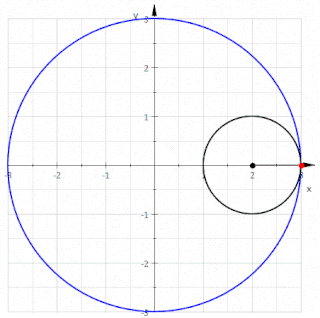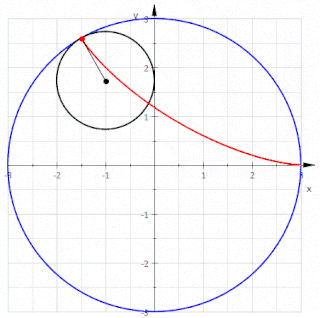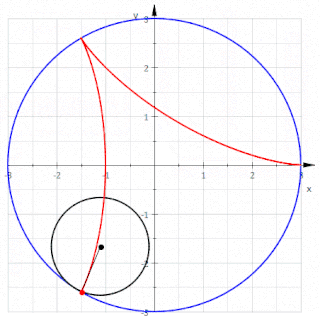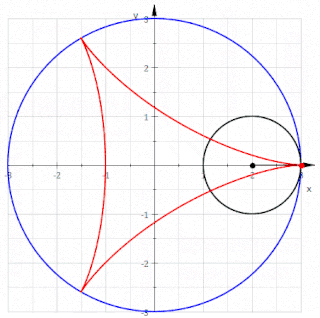
Geometride, triküspoid eğri veya Steiner eğrisi olarak da bilinen deltoid eğri, üç çentikten oluşan bir hiposikloiddir. Başka bir deyişle, bir çemberin çevresi üzerindeki bir noktanın, yarıçapının üç veya bir buçuk katı olan bir çemberin içinde kaymadan yuvarlanırken oluşturduğu yuvarlanma eğrisidir. Adını, benzediği büyük Yunanca delta (Δ) harfinden alır.



















