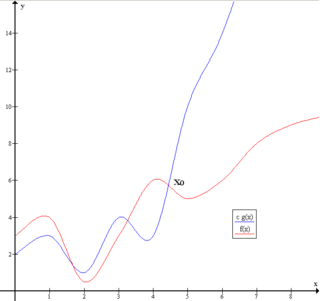
Büyük O (Big-Oh) gösterimi matematiksel bir gösterim olup işlevlerin (fonksiyonların) asimptotik davranışlarını tarif etmek için kullanılır. Bir işlevin büyümesinin asimptotik üst sınırını daha basit başka bir işlev cinsinden tanımlanması demektir. İki temel uygulama alanı vardır: matematik alanında genellikle kırpılmış bir sonsuz serinin kalan terimini karakterize etmek için kullanılır; bilgisayar bilimlerinde ise algoritmaların bilgi işlemsel karmaşıklığının çözümlemesi için kullanılır.
Yapay sinir ağları (YSA), insan beyninin bilgi işleme tekniğinden esinlenerek geliştirilmiş bir bilgi işlem teknolojisidir. YSA ile basit biyolojik sinir sisteminin çalışma şekli taklit edilir. Yani biyolojik nöron hücrelerinin ve bu hücrelerin birbirleri ile arasında kurduğu sinaptik bağın dijital olarak modellenmesidir. Nöronlar çeşitli şekillerde birbirlerine bağlanarak ağlar oluştururlar. Bu ağlar öğrenme, hafızaya alma ve veriler arasındaki ilişkiyi ortaya çıkarma kapasitesine sahiptirler. Diğer bir ifadeyle, YSA'lar, normalde bir insanın düşünme ve gözlemlemeye yönelik doğal yeteneklerini gerektiren problemlere çözüm üretmektedir. Bir insanın, düşünme ve gözlemleme yeteneklerini gerektiren problemlere yönelik çözümler üretebilmesinin temel sebebi ise insan beyninin ve dolayısıyla insanın sahip olduğu yaşayarak veya deneyerek öğrenme yeteneğidir.
Başlangıçta sonsuz küçük hesap veya "sonsuz küçüklerin hesabı" olarak adlandırılan kalkülüs, geometrinin şekillerle çalışması ve cebirin aritmetik işlemlerin genellemelerinin incelenmesi gibi, kalkülüs sürekli değişimin matematiksel çalışmasıdır.
Ayrık Fourier Dönüşümü, Fourier analizinde kullanılan özel bir Fourier dönüşümüdür.
Birleşmeli Sıralama, bilgisayar bilimlerinde 
derecesinde karmaşıklığa sahip bir sıralama algoritmasıdır. Girdi olarak aldığı diziyi en küçük hale gelene kadar ikili gruplara böler ve karşılaştırma yöntemi kullanarak diziyi sıralar.
Sıralama algoritması, bilgisayar bilimlerinde ya da matematikte kullanılan, verilen bir listenin elemanlarını belirli bir sıraya sokan algoritmadır. En çok kullanılan sıralama türleri, sayı büyüklüğüne göre sıralama ve alfabetik sıralamadır. Sıralama işleminin verimli yapılması, arama ve birleştirme algoritmaları gibi çalışması için sıralanmış dizilere gereksinim duyan algoritmaların başarımının yüksek olması için önemlidir. Sıralama algoritmaları bilgisayarlarda tutulan verilerin düzenlenmesini ve insan kullanıcı tarafından daha rahat algılanmasını da sağlar.
Hızlı Fourier dönüşümü bir dizinin ayrık Fourier dönüşümünü (DFT) ya da ters ayrık dönüşümünü hesaplayan bir algoritmadır. Fourier analizinde bir sinyal bulunduğu uzaydaki gösteriminden frekans uzayıki gösterimine ya da tersine dönüştürülür. DFT'de ise ayrık veri dizileri farklı frekans öğelerine ayrılır. Bu operasyon her ne kadar birçok alanda kullanışlı olsa da, doğrudan formüllerle hesabı hızlı ve pratik değildir; bu nedenle DFT hesabı için FFT algoritmaları kullanılmaktadır.
Poisson dağılımı, olasılık kuramı ve istatistik bilim kollarında bir ayrık olasılık dağılımı olup belli bir sabit zaman birim aralığında meydana gelme sayısının olasılığını ifade eder. Bu zaman aralığında ortalama olay meydana gelme sayısının bilindiği ve herhangi bir olayla onu hemen takip eden olay arasındaki zaman farkının, önceki zaman farklarından bağımsız oluştuğu kabul edilir.
Olasılık kuramı ve istatistik bilim dallarında üstel dağılımı bir sürekli olasılık dağılımları grubudur. Sabit ortalama değişme haddinde ortaya çıkan bağımsız olaylar arasındaki zaman aralığını modelleştirirken bir üstel dağılım doğal olarak ortaya çıkar.
Matematikte diferansiyel kalkülüs, fonksiyonların girdileri değiştikçe nasıl değiştiklerini konu alan bir kalkülüs alanıdır. Diferansiyel kalkülüsteki ana inceleme nesnesi türevdir. Oldukça yakından ilişkili diğer bir kavram da türetke ya da diferansiyeldir. Bir fonksiyonun, seçilmiş belirli bir girdi değerindeki türevi, fonksiyonun o girdi değeri yakınındaki davranışını tanımlar. Genel olarak, bir fonksiyonun belirli bir noktadaki türevi, fonksiyona o noktadaki en iyi doğrusal yaklaşımı belirler. Türev bulma işlemine "türev almak" denir. Kalkülüsün temel teoremi gereğince, türev alma işlemi integral alma işleminin tersidir.
Gustafson yasası, yeterince büyük bir sorunun verimli bir biçimde koşutlaştırılabileceğini öngören bir bilgisayar mühendisliği yasasıdır. 1988 yılında John L. Gustafson'un geliştirdiği bu kural, bir programın koşutluk derecesine bağlı olarak ne ölçüde hızlandırılabileceğini belirleyen Amdahl yasası ile yakından ilintilidir.
Sağkalım analizi, biyolojik organizmalarda ölüm ve mekanik sistemlerde başarısızlık ile ilgilenen bir istatistik dalıdır. Bu konu mühendislikte güvenilirlik teorisi veya güvenilirlik analizi, iktisat ve sosyolojide ise süre analizi veya süre modellemesi olarak adlandırılır.
Zaman serisi, istatistik, sinyal işleme, ekonometri ve finansal matematikte veri noktalarının sıklığını ifade eder ve düzenli zaman aralıklarında, ardışık zaman alanlarında tipik olarak ölçülür. Zaman serisine örnek olarak, İMKB endeksinin günlük kapanış değeri veya Türkiye'deki Kızılırmak nehrinin yıllık akış hacmi (debisi) verilebilir. Zaman serisi analizi, anlamlı istatistikleri ve verinin diğer istatistiklerini almak için birkaç yöntemi vardır. Zaman serisi tahmini önceden bilinen olayları baz alarak gelecek olayları tahmin etmenin kavramsal modelidir. Ekonometride zaman serisi tahminine bir örnek, önceki başarımlarına (performanslarına) bakarak bir hisse senedinin açılış fiyatını öngörmektir.
Algoritma analizi veya diğer adıyla algoritma çözümlemesi, bilgisayar biliminde bir algoritmayı çalıştırabilmek için gereken kaynakların miktarının tespitidir. Algoritmaların çoğunluğu, rastgele seçilmiş uzunluktaki girdiler ile çalışmak için tasarlanmıştır. Genellikle, bir algoritmanın verimlilik veya çalışma zamanı, adımların sayısı veya depolama yerleri 'nin girdi uzunluğuyla ilişkili olan işlev olarak ifade edilir.
Kriptografik özet fonksiyonu çeşitli güvenlik özelliklerini sağlayan bir özet fonksiyonudur. Veriyi belirli uzunlukta bir bit dizisine, (kriptografik) özet değerine, dönüştürür. Bu dönüşüm öyle olmalıdır ki verideki herhangi bir değişiklik özet değerini değiştirmelidir. Özetlenecek veri mesaj, özet değeri ise mesaj özeti veya kısaca özet olarak da adlandırılır.
Sayı teorisinde, asal çarpanlara ayırma bir bileşik sayının, çarpıldıklarında yine aynı sayıyı verecek şekilde, bir ve kendisi dışındaki bölenlerine ayrılmasıdır.
Matematikte, özellikle soyut cebir ve uygulamalarında, ayrık logaritma, genel logaritmanın grup kuramındaki karşılığıdır. Genel olarak bakıldığında, loga(b) ifadesi, ax = b ifadesinin gerçel sayılar kümesi içindeki çözümlerine karşılık gelir. Benzer olarak, g ve h sonlu devirli grup G'nin elemanları olduğunda, gx = h ifadesinin çözümü olan x sonuçlarına h'nin g tabanındaki ayrık logaritması denir.
Doğrusal filtreler, işleme sokulan verilerin doğrusal değişkenler ile işlendiği sinyal işleme yapılarıdır. Bir başka deyişle, elde edilen sinyal çıktısı, girdinin doğrusal katsayılar ile işleme sokulması ile oluşturulur. Bu özellikte filtreler ile oluşturulan sistemler, dolayısıyla doğrusal sinyal tepkisi yaratırlar.
Parametre belirli bir sistemi tanımlamak veya sınıflandırmak için yardımcı olabilecek herhangi bir özellik. Parametre, sistemi tanımlarken veya performansını, durumunu değerlendirirken yararlı veya kritik olan bir sistem unsurudur.
Matematikte, çok değişkenli karmaşık analiz ya da çok boyutlu karmaşık analiz, karmaşık koordinat uzayı 
de ya da bu uzayın altkümeleri üzerinde tanımlı ve karmaşık değer alan fonksiyonların teorisi; yani, birden fazla karmaşık değişkenli fonksiyonların teorisidir.
