
Bir üçgen düzlemde birbirine doğrusal olmayan üç noktayı birleştiren üç doğru parçasının birleşimidir. Üçgene müselles ve üçbucak da denir.

Grup teorisi veya Grup kuramı, simetrileri inceleyen matematik dalıdır. Simetri kuramı olarak da adlandırılabilir. Bir nesnenin simetrileri ile kast edilen, nesneye uygulandığında nesneye hiçbir etki olmamış gibi sonuç veren dönüşümlerdir. Her nesnenin en az bir simetrisi vardır: hiçbir şey yapmadan olduğu gibi bırakma dönüşümü. Bahsettiğimiz dönüşümlerin tersleri de vardır ve aradığımız özellikleri sağlarlar. Son olarak da dönüşümlerin art arda yapılması, birleşimli bir işlemdir. Bu üç koşula sırasıyla birim elemana sahip olma, elemenların tersi olma ve grup işleminin birleşmeli olması denir. Bu kavramların matematikte soyutlanması, üzerinde tersinebilir ve bileşme özelliğine sahip ikili bir işlemin tanımlı olduğu kümeler ile yapılır. Daha detaylı açıklamak gerekirse, grup nesnesi bir küme G ve onun üzerinde tanımlı bir  işleminden oluşur. Bu operasyonun aşağıdaki şartları sağlaması gereklidir:
işleminden oluşur. Bu operasyonun aşağıdaki şartları sağlaması gereklidir:

Küresel yıldız kümesi, galaksi merkezi etrafında uydu gibi dolanan, yıldızların küresel bir bileşimidir. Küresel yıldız kümeleri yerçekimi ile bir arada durabilirler. Yerçekimi sayesinde küresel bir şekle ve göreceli olarak merkeze doğru artan bir madde yoğunluğuna sahiplerdir. Yıldız kümesinin bir alt kategorisi olan küresel yıldız kümesi, Latince bir sözcük olan ve küçük küre anlamına gelen globulus kelimesinden türetilmiştir.
Yüzey, matematikte ve özellikle topolojide iki boyutlu çokkatlı. İki gerçel değişkenli ve gerçel değerli bir fonksiyonun üç boyutlu uzayda (R³) grafiği tipik yüzey örneğidir. Ayrıca Dünya yüzeyi, bir yumurtanın kabuğu, bir simit birer yüzeydir.

Matematikte karmaşık düzlem, gerçel eksen ve ona dik olan sanal eksen tarafından oluşturulmuş, karmaşık sayıların geometrik bir gösterimidir. Karmaşık sayının gerçel kısmının x-ekseni boyuncaki yer değiştirmeyle, sanal kısmının ise y-eksenindeki yer değiştirmeyle temsil edildiği değiştirilmiş bir Kartezyen düzlem olarak düşünülebilir.
Matematikte, birkaç fonksiyon ya da fonksiyon gruplarının kendi isimleri yeterli öneme layıktır. Bu makaleler fonksiyonları açıklamak için olan daha ayrıntılı olarak gösteren bir listedir. İstatistik dışı ve matematiksel fizik gelişmeleri sonucu özel fonksiyonlar büyük bir teori olmuştur. Modern bir, soyut incelik fonksiyon uzayıları geniş karşılaştırma görünümü, sonsuz-boyutlu ve 'isimsiz' fonksiyonlar içindeki ve simetri ya da ilişki harmonik analiz ve grup temsilileri gibi özellikler ile özel fonksiyonlar ile seçilmiştir.
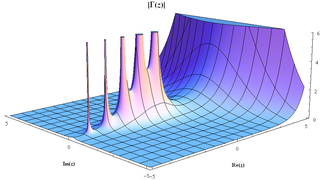
Meromorf fonksiyon, özellikle karmaşık analizde, bir fonksiyon çeşidi. Daha açık bir ifadeyle, meromorf fonksiyon, karmaşık düzlemin açık bir D kümesi üzerinde fonksiyonun kutup noktalarından oluşan belli bir korunmalı noktalar kümesi haricinde D 'nin geriye kalan diğer noktalarının tümünde holomorf olan fonksiyondur. Meromorf kelimesi Yunanca "kısım", "parça" anlamına gelen “meros” ve "tüm", "bütün" anlamına gelen “holos” kelimelerinin tezat bir birleşiminden ortaya çıkmış bir kelimedir.

Matematikte bir döşeme, aralarında boşluk bırakmadan veya örtüşmeden bir düzlemi kaplayan düzlemsel şekiller kümesidir. Bu kavram daha yüksek boyutlar için de genellenebilir, bu genişletilmiş anlamı için döşeme yerine tesselasyon terimi kullanılır. Tesselasyon M. C. Escher'in eserlerinde sıkça görülebilir. Tesselasyona sanat tarihi boyunca, antik mimariden modern sanata kadar rastlanabilir.

Pergel ve çizgilik çizimi, belli uzunlukta doğrular, belli büyüklükte açılar ve diğer geometrik şekilleri çizmek için sadece ideal bir çizgilik ve pergel kullanılmasıdır.

Serbest yüzey, bir akışkanın yüzeyinde normal gerilmenin sabit ve kayma gerilmesinin sıfır olduğu yüzey bölgesine denir. İki ayrı homojen akışkanın temas sınırı örnek olarak verilebilir: sıvı su ile atmosferdeki hava arasında. Sıvıların aksine, gazlar serbest yüzey oluşturamazlar. Bunun sebebi, gazların bulundukları ortamı, ne kadar büyük olursa olsun, genleşerek doldurmak istemeleridir.
Bu diferansiyel geometri konuların bir listesidir. Ve aynı zamanda Lie grubu konularının listesi metrik geometri ve diferansiyelin sözlüğü bkz.
Matematikte açık birim disk, P noktasına uzaklığı 1'den küçük noktalar kümesidir.
Bu, "Antik Yunan matematikçilerinin zaman çizelgesi"dir..
Bu sayfa teoremlerin bir listesidir. Ayrıca bakınız:
- Sonlu basit grupların sınıflandırılması
- Temel teoremlerin listesi
- Yardımcı teoremler listesi
- Varsayımların listesi
- Eşitsizliklerin listesi
- Matematiksel kanıtların listesi
- Yanlış adlandırılmış teoremlerin listesi
Matematik konularının listesi, matematik ile ilgili çeşitli konuları kapsar. Bu listelerden bazıları yüzlerce makaleye bağlantı içerir; bazıları sadece birkaç tane ile bağlantılıdır. Bu makale, aynı içeriği, göz atmaya daha uygun bir şekilde organize halde bir araya getirmektedir. Listeler, temel ve ileri matematik, metodoloji, matematiksel ifadeler, integraller, genel kavramlar, matematiksel nesneler ve referans tablolarının özelliklerini kapsar. Ayrıca insanların adını taşıyan denklemleri, matematiksel toplulukları, matematikçileri, matematik dergilerini ve meta listeleri de kapsar.

Christian Felix Klein, grup teorisi, karmaşık analiz, Öklid dışı geometri ve geometri ile grup teorisi arasındaki ilişkiler üzerine yaptığı çalışmalarla tanınan Alman matematikçi ve matematik eğitimcisi. Klein'ın geometrileri temel simetri gruplarına göre sınıflandıran 1872 Erlangen programı, döneminin matematiğinin büyük kısmının etkili bir senteziydi.
Bu, matematikte kullanılan eğrilerin Vikipedi makalelerine göre bir galerisidir. Ayrıca bakınız eğriler listesi.
Bu, farklı alanlarda kullanılan eğriler hakkındaki Vikipedi makalelerinin bir listesidir: matematik, fizik, mühendislik, ekonomi, tıp, biyoloji, psikoloji, ekoloji, vb.

Düzlem ve katenoidden sonra helis yüzey de denen helikoid bilinen üçüncü minimal yüzeydir. Helikoid, helis ve eksenle tanımlanan yüzeydir.

Dünya'nın şekli, jeodezide, Dünya gezegenini modellemek için kullanılan kimi boyut ve şekillerdir. Şekil türü, model için gereken hassasiyet dahil olmak üzere, çoğunlukla uygulama alanına dayalı olarak farklılaşmaktadır. Küresel şekilli bir Dünya diğer birçok amaçla birlikte coğrafya ve astronomi için tatmin edici olan genel kabul görmüş tarihsel bir yaklaşımdır. Oldukça kesinliğe sahip olan kimi modeller zaman içinde geliştirilmiş olup, böylece koordinat sistemleri navigasyon, yerölçme, kadastro, arazi kullanımı ve diğer çeşitli konuların kesin ihtiyaçlarına hizmet edebilir hale gelmiştir.











