Yuvarlanma eğrisi
Eğrilerin diferansiyel geometrisinde, bir rulet veya yuvarlanma eğrisi (İngilizce: roulette), sikloidler, episikloidler, hiposikloidler, trokoidler, epitrokoidler, hipotrokoidler ve gereçleri (involütleri) genelleştiren bir eğri türüdür.
Tanım
Gayriresmî tanım

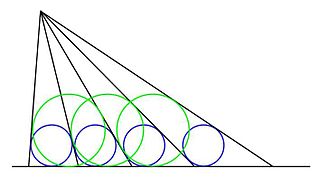
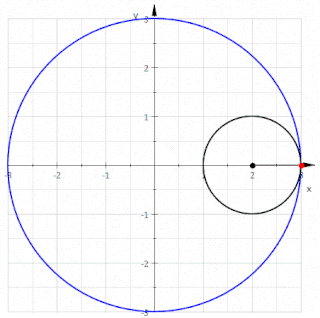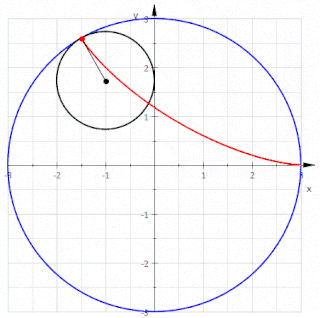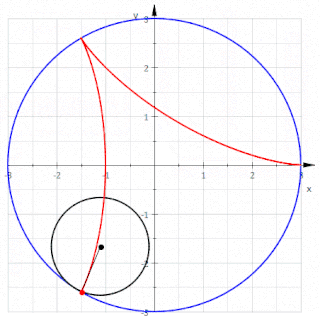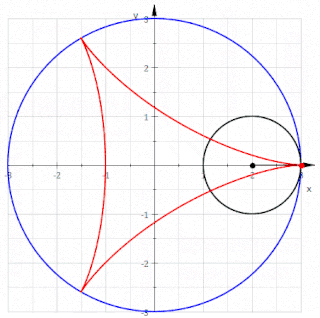
Kabaca ifade etmek gerekirse, yuvarlanma eğrisi, belirli bir eğriye bağlı bir nokta ("üreteç" veya "kutup" olarak adlandırılır) tarafından, bu eğri sabit olan ikinci bir eğri boyunca kaymadan yuvarlanırken tanımlanan eğridir. Daha açık bir ifadeyle, hareketli bir düzleme bağlı bir eğri verildiğinde, eğri aynı alanı işgal eden sabit bir düzleme bağlı belirli bir eğri boyunca kaymadan yuvarlanır, o zaman hareketli düzleme bağlı bir nokta, sabit düzlemde yuvarlanma eğrisi veya rulet adı verilen bir eğriyi tanımlar.
Özel durumlar ve ilgili kavramlar
Yuvarlanan eğrinin bir doğru ve üretecin doğru üzerinde bir nokta olduğu durumda, yuvarlanma eğrisi sabit eğrinin bir involütü olarak adlandırılır. Eğer yuvarlanan eğri bir çember ve sabit eğri bir doğru ise, o zaman yuvarlanma eğrisi bir trokoiddir. Eğer bu durumda, nokta çember üzerinde yer alıyorsa, yuvarlanma eğrisi bir sikloiddir.
İlgili bir kavram glissette, verilen bir eğriye bağlı bir noktanın verilen iki (veya daha fazla) eğri boyunca kayarken tanımladığı eğridir.
Resmi tanım
Biçimsel olarak, eğriler Öklid düzleminde diferansiyellenebilir eğriler olmalıdır. "Sabit eğri" değişmez tutulur; "yuvarlanan eğri" bir sürekli kongrüans dönüşümüne tabi tutulur, öyle ki her zaman eğriler, her iki eğri boyunca alındığında aynı hızla hareket eden bir temas noktasında teğet olurlar (bu kısıtlamayı ifade etmenin başka bir yolu da iki eğrinin temas noktasının kongrüans dönüşümünün anlık dönme merkezi olmasıdır). Ortaya çıkan yuvarlanma eğrisi, aynı uyum dönüşümleri kümesine tabi tutulan üretecin locusu tarafından oluşturulur.
Orijinal eğrileri karmaşık düzlemde eğriler olarak modelleyerek, , yuvarlanan () ve sabit () eğrilerinin iki doğal parametrizasyonları olsun, öyle ki , ve tüm için. üzerinde yuvarlandıkça üretecinin yuvarlanma eğrisi daha sonra aşağıdaki eşleme tarafından verilir:
Genellemeler
Yuvarlanan eğriye tek bir nokta yerine, verilen başka bir eğri hareketli düzlem boyunca taşınırsa, bir uyumlu eğriler ailesi üretilir. Bu ailenin zarfı yuvarlanma eğrisi veya rulet olarak da adlandırılabilir.
Daha yüksek uzaylarda yuvarlanma eğrileri kesinlikle hayal edilebilir ancak teğetlerden daha fazlasını hizalamak gerekir.
Örnek
Eğer sabit eğri bir zincir eğrisi (İngilizce: catenary) ve yuvarlanan eğri (İngilizce: roulette) bir doğru ise, şu sonuca varırız:
Doğrunun parametrelendirilmesi şu şekilde seçilir:
Yukarıdaki formülü uygulayarak şunu elde ederiz:
Eğer p = -i ise ifadenin sabit bir hayali kısmı vardır (yani -i) ve rulet yatay bir çizgidir. Bunun ilginç bir uygulaması, bir kare tekerleğin zincir eğrisi yaylarının eşleştirilmiş bir serisi olan bir yolda zıplamadan yuvarlanabilmesidir.
Yuvarlanma eğrileri listesi
| Sabit eğri | Hareketli eğri | Üreteç noktası | Rulet (Yuvarlanma eğrisi) |
|---|---|---|---|
| Herhangi bir eğri | Doğru | Doğru üzerinde bir nokta | Eğrinin involutü |
| Doğru | Herhangi | Herhangi | Siklogon |
| Doğru | Çember | Herhangi | Trokoid |
| Doğru | Çember | Çember üzerinde bir nokta | Sikloid |
| Doğru | Konik kesit | Koniğin merkezi | Sturm yuvarlanan eğrisi[2] |
| Doğru | Konik kesit | Koniğin odağı | Delaunay yuvarlanan eğrisi[3] |
| Doğru | Parabol | Parabolün odağı | Zincir eğrisi[4] |
| Doğru | Elips | Elipsin odağı | Eliptik zincir eğrisi[4] |
| Doğru | Hiperbol | Hiperbolün odağı | Hiperbolik zincir eğrisi[4] |
| Doğru | Hiperbol | Hiperbolün merkezi | Dikdörtgen elastika[2][] |
| Doğru | Siklosikloid | Merkez | Elips[5] |
| Çember | Çember | Herhangi | Ortalanmış trokoid[6] |
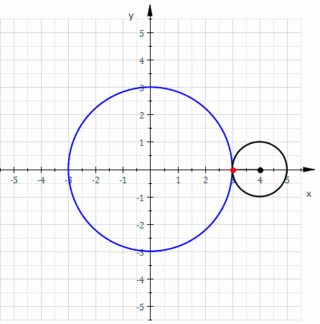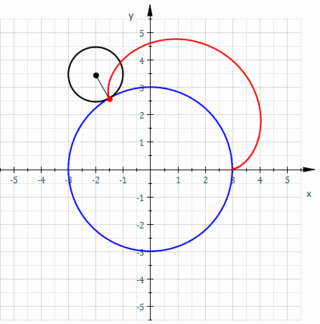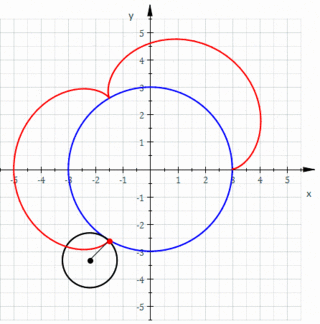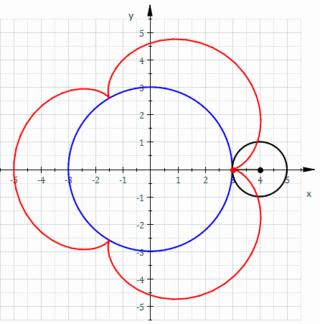
| Bir çemberin dışında | Çember | Herhangi | Epitrokoid |
| Bir çemberin dışında | Çember | Çemberin üzerinde bir nokta | Episikloid |
| Bir çemberin dışında | Aynı yarıçaplı çember | Herhangi | Limaçon |
| Bir çemberin dışında | Aynı yarıçaplı çember | Çemberin üzerinde bir nokta | Kardioid |
| Bir çemberin dışında | Yarıçapın yarısı kadar çember | Çemberin üzerinde bir nokta | Nefroid |
| Bir çemberin içinde | Çember | Herhangi | Hipotrokoid |
| Bir çemberin içinde | Çember | Çemberin üzerinde bir nokta | Hiposikloid |
| Bir çemberin içinde | Yarıçapın üçte biri kadar çember | Çemberin üzerinde bir nokta | Deltoid |
| Bir çemberin içinde | Yarıçapın dörtte biri kadar çember | Çemberin üzerinde bir nokta | Astroid |
| Parabol | Ters yönde parametrelendirilmiş eşit parabol | Parabolün tepe noktası | Diocles Sisoidi[1] |
| Zincir eğrisi | Doğru | Bkz. yukarıdaki örnekler | Doğru |
Ayrıca bakınız
Notlar
- ^ a b ""Cissoid" on www.2dcurves.com". 30 Kasım 2022 tarihinde kaynağından arşivlendi. Erişim tarihi: 22 Aralık 2023.
- ^ a b ""Sturm's roulette" on www.mathcurve.com". 16 Eylül 2019 tarihinde kaynağından arşivlendi. Erişim tarihi: 22 Aralık 2023.
- ^ ""Delaunay's roulette" on www.mathcurve.com". 13 Eylül 2019 tarihinde kaynağından arşivlendi. Erişim tarihi: 22 Aralık 2023.
- ^ a b c ""Delaunay's roulette" on www.2dcurves.com". 12 Şubat 2019 tarihinde kaynağından arşivlendi. Erişim tarihi: 22 Aralık 2023.
- ^ ""Roulette with straight fixed curve" on www.mathcurve.com". 13 Eylül 2019 tarihinde kaynağından arşivlendi. Erişim tarihi: 22 Aralık 2023.
- ^ ""Centered trochoid" on mathcurve.com". 21 Eylül 2019 tarihinde kaynağından arşivlendi. Erişim tarihi: 22 Aralık 2023.
Kaynakça
- W. H. Besant (1890) Notes on Roulettes and Glissettes from Cornell University Historical Math Monographs, originally published by Deighton, Bell & Co.
- Eric W. Weisstein, Roulette (MathWorld)