Yörünge bölgesini temizleme

Görselde, iç Güneş Sistemi'ndeki nesnelerin dağılımı şematik olarak gösterilmiştir. Gezegenlerin yörüngelerinde bulunan nesnelerin sayısı ile ana asteroit kuşağındaki nesnelerin sayısı arasındaki fark dikkat çekicidir. Soter tarafından önerilen gezegen ayrımını hesaplamak için iki bilgiye ihtiyaç vardır: Belirli bir yörünge bölgesinde bulunan nesnelerin sayısı ve kütleleri. Bu harita ise bunlardan yalnızca birini sunmaktadır. Bu durum, özellikle Jüpiter'in yörüngesinde bulunan nesnelerin dağılımına bakıldığında belirgindir. Gezegenin kütle çekimi tarafından yörüngelerinde hapsedilen Truva asteroitleri (yeşil renkte), sayıca oldukça fazladır (bir milyondan fazla), fakat toplam kütleleri Jüpiter'in kütlesinin yaklaşık 3 × 10^-7'si kadardır.

"Yörünge bölgesini temizleme" (veya dinamik baskınlık, İngilizce: dynamical dominance), bir gök cisminin yörüngesi etrafında kütleçekimsel olarak baskın hale gelmesini ve doğal uyduları ya da kütleçekimsel etkisi altında olanlar dışında, kendi boyutuna yakın başka hiçbir cismin yörüngesinde bulunmamasını tanımlar.

"Yörünge bölgesini temizleme", Uluslararası Astronomi Birliği (IAU) tarafından 2006 yılında kabul edilen tanıma göre, bir gök cisminin Güneş Sistemi'nde gezegen olarak kabul edilmesi için gerekli üç koşuldan biridir.^[1] 2015 yılında bu tanımın ötegezegenleri kapsayacak şekilde genişletilmesi önerilmiştir.^[2]

Tanıma göre bir gezegen, oluşumunun son aşamalarında "yörünge bölgesini temizlemiş" olur, yani benzer boyutlardaki diğer cisimleri ortadan kaldırmıştır. Diğer gezegen olma kriterlerini karşılayan, fakat yörünge bölgesini temizlememiş olan büyük bir cisim ise cüce gezegen olarak sınıflandırılır. Bu duruma, yörüngesi Neptün'ün yörüngesiyle kesişen ve Kuiper Kuşağı'ndaki birçok cisimle yörünge komşuluğunu paylaşan Plüton da dahildir. IAU'nun tanımı bu terime spesifik sayılar veya denklemler eklemez, fakat IAU tarafından tanınan tüm gezegenler, herhangi bir cüce gezegen veya cüce gezegen adayı ile karşılaştırıldığında yörünge bölgelerini çok daha büyük ölçüde (büyüklük mertebesine göre) temizlemişlerdir.^[2]

Bu ifade, gezegen bilimciler Alan Stern ve Harold F. Levison tarafından 2000 IAU genel kuruluna sunulan bir makaleden kaynaklanmaktadır. Yazarlar, bir yıldızın yörüngesinde dönen bir nesnenin, nesnenin kütlesine ve yörünge periyoduna bağlı olarak "komşu bölgesini gezegenimsilerden temizleme" olasılığını belirlemek için teorik bir temel geliştirirken birbirine benzer birkaç ifade kullandılar.^[3] Steven Soter dinamik baskınlık terimini kullanmayı tercih etmiş^[4] ve Jean-Luc Margot bunun "yanlış anlaşılmaya daha az yol açacağını" belirtmiştir.^[2]

2006 yılından önce IAU'nun gezegenleri tanımlama konusunda belirli kuralları yoktu, çünkü on yıllardır yeni bir gezegen keşfedilmemişti. Oysa asteroitler veya kuyruklu yıldızlar gibi yeni keşfedilen çok sayıda küçük cismi tanımlamak için köklü kurallar vardı. 2005 yılında keşfinin duyurulmasından sonra, boyutu Plüton ile karşılaştırılabilir olduğu için Eris'in tanımlanma süreci duraklamıştı. IAU, Eris'in tanımlanmasını çözmek için gezegenleri küçük gezegenlerden ayıran taksonomik bir tanım arayışına girmiştir.

Kriterler

Bu ifade, yörüngedeki bir cismin (bir gezegen veya öngezegen), zamanla yakınındaki daha küçük cisimlerle kütleçekimsel olarak etkileşime girerek yörünge bölgesini "süpürmesi" anlamına gelir. Birçok yörünge döngüsü boyunca, büyük bir cisim küçük cisimlerin ya kendisiyle birleşmesine ya da başka bir yörüngeye itilmelerine veya uydu olarak ya da rezonans yörüngesine yakalanmalarına neden olur. Sonuç olarak, kendi uyduları ya da kendi kütleçekimi etkisi altında olan cisimler dışında, önemli boyuttaki diğer cisimlerle yörüngesini paylaşmaz. Bu son kısıtlama, yörüngeleri kesişebilen fakat yörüngesel rezonans nedeniyle birbirleriyle asla çarpışmayacak olan Jüpiter ve truvalıları, Dünya ve 3753 Cruithne ya da Neptün ve plütinolar gibi cisimleri hariç tutmaktadır.^[3] Yörüngenin ne kadar temizlenmesi gerektiği konusunda Jean-Luc Margot, "Bir gezegen hiçbir zaman yörünge bölgesini tamamen temizleyemez, çünkü kütleçekimsel ve ışınımsal kuvvetler sürekli olarak asteroitlerin ve kuyruklu yıldızların yörüngelerini gezegen yörüngesiyle kesişecek şekilde bozar" diye vurgular ve IAU'nun kusursuz yörünge temizliği gibi imkansız bir standardı amaçlamadığını belirtir.^[2]

Stern–Levison'un $Λ$ parametresi

Stern ve Levison makalelerinde, "gezegensel cisimlerin çevrelerindeki bölgeyi ne kadar kontrol ettiklerini" belirlemek için bir algoritma aradılar.^[3] $Λ$ (lambda), bir cismin evrenin yaşı kadar bir süre boyunca (Hubble zamanı) daha küçük kütleleri yörünge bölgesinden dışarıya saçma yeteneğini ölçen bir kavramdır. $Λ$ , boyutsuz bir sayı olarak şu şekilde tanımlanır:

$\Lambda ={\frac {m^{2}}{a^{3/2}}},k$

burada $m$ cismin kütlesi, $a$ cismin yarı-büyük ekseni (yörüngesinin en geniş çapı) ve $k$ ise saçılan küçük cismin yörünge öğelerinin ve ne kadar saçılması gerektiğinin bir fonksiyonudur. Güneş Sistemi'ndeki gezegen diski alanında, küçük cisimlerin Güneş'e belirli bir mesafedeki ortalama $k$ değerlerinde çok az değişiklik görülür.^[4]

Eğer $Λ$ > 1 ise, cisim muhtemelen yörünge bölgesindeki küçük cisimleri temizleyecektir. Stern ve Levison bu ayırt edici parametreyi kullanarak, kütleçekimsel olarak yuvarlak ve Güneş etrafında dönen cisimleri, "komşu gezegenimsi cisimleri dinamik olarak yeterince temizlemiş" olan überplanets (üst gezegenler) ve bu kritere uymayanları ise unterplanets (alt gezegenler) olarak ayırdılar. Üst gezegenler, Güneş'in etrafında dönen en büyük sekiz cisimdir (yani IAU gezegenleri) ve alt gezegenler de geri kalanıdır (yani IAU cüce gezegenleri).

Soter'in $μ$ ayırıcısı

Steven Soter, yıldızların yörüngesinde dönen cisimleri gezegenler ve gezegen olmayanlar olarak ayırmak için gözleme dayalı bir ölçü olarak $μ$ 'yu (mu) önerdi ve buna "gezegensel ayırt edici" adını verdi.^[4] $μ$ şu şekilde tanımlanır: $\mu ={\frac {M}{m}}$ burada $μ$ boyutsuz bir parametredir, $M$ aday gezegenin kütlesi ve $m$ ise aynı yörünge bölgesini paylaşan tüm diğer cisimlerin kütlesidir, yani yörüngeleri birincil cisme olan ortak bir radyal mesafeyi kesen ve rezonans dışı periyotları bir büyüklük mertebesinden daha az farklılık gösteren tüm cisimlerin kütlesidir.^[4]

Periyotların büyüklük mertebesindeki benzerlik kuyruklu yıldızları bu hesaplamadan hariç tutar, fakat kuyruklu yıldızların toplam kütlesi diğer küçük Güneş Sistemi cisimleriyle karşılaştırıldığında önemsizdir. Bu nedenle, dahil edilmeleri sonuçlar üzerinde büyük bir etki yapmaz. μ, aday cismin kütlesinin, yörünge bölgesini paylaşan diğer cisimlerin toplam kütlesine bölünmesiyle hesaplanır. Bu, yörünge bölgesinin gerçek temizlenme derecesinin bir ölçüsüdür. Soter, $μ$ > 100 ise aday cismin gezegen olarak değerlendirilmesini önermiştir.^[4]

Margot'nun $Π$ ayırıcısı

Astronom Jean-Luc Margot sadece bir cismin kendi kütlesine, yarı-büyük eksenine ve yıldızın kütlesine dayanarak bir cismi kategorize edebilen $Π$ (pi) adında ayırt edici bir parametre önerdi.^[2] Stern–Levison'un $Λ$ 'sı gibi, $Π$ de bir cismin yörüngesini temizleme yeteneğinin bir ölçüsüdür, fakat $Λ$ 'dan farklı olarak tamamen teorik bir temele dayanır ve Güneş Sistemi'nden ampirik veriler kullanmaz. $Π$ , Soter'in yörünge bölgesinin doğru bir sayımını gerektiren $μ$ 'sinin aksine, gezegen dışı cisimler için bile uygun şekilde belirlenebilir özelliklere dayanır.

$\Pi ={\frac {m}{M^{5/2}a^{9/8}}},k$

burada $m$ aday cismin kütlesi (Dünya kütlesi olarak), $a$ cismin yarı-büyük ekseni (AU olarak), $M$ ana yıldızın kütlesi (Güneş kütlesi olarak) ve $k$ ise $Π$ > 1 olan ve yörüngesini temizleyebilen bir cisim için seçilmiş bir sabittir. $k$ , istenen temizlenme derecesine ve bu işlemi gerçekleştirmek için gereken zamana bağlıdır. Margot, temizlenme derecesini $2{\sqrt {3}}$ Hill yarıçapı kadar ve ana yıldızın ana koldaki ömrünü (yıldızın kütlesine bağlı olarak) zaman limiti olarak seçmiştir. Bu birimlerde ve 10 milyar yıllık ana kol ömründe, $k$ = 807'dir.^[a] Gök cismi, $Π$ > 1 ise bir gezegen olarak kabul edilir. Verilen yörüngede temizlenmesi gereken minimum kütle, $Π$ = 1 olduğunda elde edilir.

$Π$ , aday cismin yakındaki bir yörüngedeki küçük bir cisme, daha küçük cismin istenen yörünge mesafesinden temizlenecek kadar enerji iletmesi için gereken yörünge sayısının hesaplamasına dayanır. Bu, asteroit kuşağındaki asteroitler için gereken temizlenme sürelerinin ortalamasını kullanan $Λ$ 'dan farklıdır ve bu nedenle Güneş Sistemi'nin bu bölgesine yöneliktir. $Π$ 'nin anakol ömrünü kullanması, cismin nihayetinde yıldızın etrafındaki bir yörüngeyi temizleyeceği anlamına gelir; $Λ$ 'nın bir Hubble zamanı kullanması, cismin yörüngesini gerçekten temizlemeden önce yıldızın gezegen sistemini bozabileceği (örneğin nova olarak) anlamına gelir.

$Π$ formülü dairesel bir yörünge varsayar. Eliptik yörüngelere uyarlanması gelecek çalışmalara bırakılmıştır, fakat Margot bunun dairesel yörüngelerle aynı büyüklük mertebesine sahip olmasını beklemektedir.

2024 yılında, Kahverengi cücelerin etrafındaki gezegenleri hesaba katmak için 10 milyar yıllık tek tip bir temizleme zaman ölçeğine sahip güncellenmiş bir kriter yayımlandı.^[5] Güneş Sistemi cisimleri için $Π$ değerleri değişmeden kalmıştır.

Sayısal değerler

Aşağıda, Margot'nun gezegen ayırıcısı $Π$ 'ye göre azalan sırayla sıralanmış gezegenler ve cüce gezegenlerin listesi bulunmaktadır.^[2] IAU tarafından tanımlanan sekiz gezegenin tümü için $Π$ , 1'den çok daha büyük magnitüdlerdeyken (büyüklük), tüm cüce gezegenler için $Π$ , 1'den çok daha küçük magnitüdlerde bulunur. Ayrıca Stern–Levison'un $Λ$ 'sı ve Soter'in $μ$ 'si de listelenmiştir. Yine, gezegenler $Λ$ için 1'den çok daha büyük ve $μ$ için 100'den çok daha büyüktür, cüce gezegenler ise $Λ$ için 1'den çok daha küçük ve $μ$ için 100'den çok daha küçüktür. Ayrıca, $Π$ = 1 ve $Λ$ = 1 olduğu mesafeler de gösterilmiştir (burada cisim gezegen olmaktan cüce gezegen olmaya geçiş yapar).

Sedna'nın kütlesi bilinmemektedir; burada yaklaşık 2 g/cm³'lük bir yoğunluk varsayımıyla çok kabaca 10²¹ kg olarak tahmin edilmiştir.

Sıra	İsim	Margot'nun gezegensel ayırıcısı $Π$	Soter'in gezegensel ayırıcısı $μ$	Stern–Levison $Λ$ parametresi ^[b]	Kütle (kg)	Nesne türü	$Π$ = 1 uzaklık (AU)	$Λ$ = 1 uzaklık (AU)
1	Jüpiter	&0000000000040115.00000040.115	6,25×10⁵	1,30×10⁹	1,8986×10²⁷	5. gezegen	&0000000000064000.00000064.000	&0000000006220000.0000006.220.000
2	Satürn	&0000000000006044.0000006.044	1,9×10⁵	4,68×10⁷	5,6846×10²⁶	6. gezegen	&0000000000022000.00000022.000	&0000000001250000.0000001.250.000
3	Venüs	&0000000000000947.000000947	1,3×10⁶	1,66×10⁵	4,8685×10²⁴	2. gezegen	&0000000000000320.000000320	&0000000000002180.0000002.180
4	Dünya	&0000000000000807.000000807	1,7×10⁶	1,53×10⁵	5,9736×10²⁴	3. gezegen	&0000000000000380.000000380	&0000000000002870.0000002.870
5	Uranüs	&0000000000000423.000000423	2,9×10⁴	3,84×10⁵	8,6832×10²⁵	7. gezegen	&0000000000004100.0000004.100	&0000000000102000.000000102.000
6	Neptün	&0000000000000301.000000301	2,4×10⁴	2,73×10⁵	1,0243×10²⁶	8. gezegen	&0000000000004800.0000004.800	&0000000000127000.000000127.000
7	Merkür	&0000000000000129.000000129	9,1×10⁴	1,95×10³	3,3022×10²³	1. gezegen	&0000000000000029.00000029	&0000000000000060.00000060
8	Mars	&0000000000000054.00000054	5,1×10³	9,42×10²	6,4185×10²³	4. gezegen	&0000000000000053.00000053	&0000000000000146.000000146
9	Ceres	0,04	0,33	8,32×10^-4	9,43×10²⁰	cüce gezegen	&0000000000000000.1600000,16	&-1000000000000000.0240000,024
10	Plüton	0,028	0,08	2,95×10^-3	1,29×10²²	cüce gezegen	&0000000000000001.7000001,70	&0000000000000000.8120000,812
11	Eris	0,020	0,10	2,15×10^-3	1,67×10²²	cüce gezegen	&0000000000000002.1000002,10	&0000000000000001.1300001,130
12	Haumea	0,0078	0,02^[6]	2,41×10^-4	4,0×10²¹	cüce gezegen	&0000000000000000.5800000,58	&0000000000000000.1680000,168
13	Makemake	0,0073	0,02^[6]	2,22×10^-4	~4,0×10²¹	cüce gezegen	&0000000000000000.5800000,58	&0000000000000000.1680000,168
14	Quaoar	0,0027	0,007^[6]		1,4×10²¹	cüce gezegen
15	Gonggong	0,0021	0,009^[6]		1,8×10²¹	cüce gezegen
16	Orcus	0,0014	0,003^[6]		6,3×10²⁰	cüce gezegen
17	Sedna	~0,0001	<0,07^[7]	3,64×10^-7	?	cüce gezegen

İtiraz

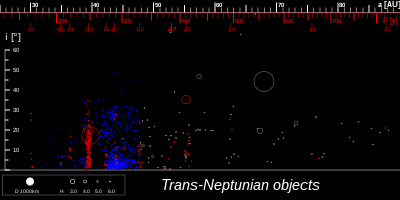
Plüton'a yönelik New Horizons görevinin baş araştırmacısı Stern, Plüton'un çevresini temizleyememesi nedeniyle yeniden sınıflandırılmasına karşı çıktı. IAU'nun ifadesinin belirsiz olduğunu ve -Plüton gibi- Dünya, Mars, Jüpiter ve Neptün'ün de yörüngelerindeki bölgeyi temizlemediklerini savundu. Dünya, 10.000 Dünya'ya yakın asteroit (NEA) ile aynı yörüngede döner ve Jüpiter'in yörünge yolunda 100.000 Truvalı vardır. Ayrıca, "Neptün bölgesini temizlemiş olsaydı, Plüton orada olmazdı" demiştir.^[8]

IAU'nun 'gezegenler' kategorisi, Stern'in kendi önerdiği 'überplanets' (üst gezegenler) kategorisiyle neredeyse aynıdır. Stern ve Levison'un $Λ$ ayrımını öneren makalede, "bir üst gezegeni, bir yıldızın etrafındaki yörüngede bulunan ve komşu gezegenimsileri temizleyecek kadar dinamik açıdan önemli olan bir gezegensel cisim olarak tanımlarız..." diye belirtmişler ve birkaç paragraf sonra da "Dinamik bir bakış açısından, güneş sistemimiz açıkça 8 üst gezegen içerir" demişlerdir (Dünya, Mars, Jüpiter ve Neptün dahil).^[3] Stern bunu gezegenlerin dinamik alt kategorilerini tanımlamak için önermiş olsa da, gezegenlerin tanımında dinamik ilişkiler yerine içsel özelliklerin kullanılması gerektiğini savunarak bunu reddetmiştir.^[9]

Ayrıca bakınız

Notlar

^ $k$ için bu ifade Margot'un makalesi takip edilerek aşağıdaki gibi türetilebilir: $P$ yörünge periyoduna sahip $M$ kütleli bir cismin yörüngesinde dönen $m$ kütleli bir cisim için gereken zaman: $t_{\text{clear}}=P{\frac {\delta x^{2}}{D_{x}^{2}}}$ burada $\delta x\simeq {\frac {C}{a}}\left({\frac {m}{3M}}\right)^{1/3},D_{x}\simeq {\frac {10}{a}}{\frac {m}{M}},P=2\pi {\sqrt {\frac {a^{3}}{GM}}},$ ve $C$ temizlenmesi gereken Hill yarıçaplarının sayısıdır. Bu, şu sonucu verir: $t_{\text{clear}}=2\pi {\sqrt {\frac {a^{3}}{GM}}}{\frac {C^{2}}{a^{2}}}\left({\frac {m}{3M}}\right)^{2/3}{\frac {a^{2}M^{2}}{100m^{2}}}={\frac {2\pi }{100{\sqrt {G}}}}{\frac {C^{2}}{3^{2/3}}}a^{3/2}M^{5/6}m^{-4/3}$ temizleme süresinin $t_{\text{clear}}$ karakteristik bir zaman ölçeğinden $t_{*}$ daha az olmasını gerektirir: $t_{*}\geq t_{\text{clear}}=2\pi {\sqrt {\frac {a^{3}}{GM}}}{\frac {C^{2}}{a^{2}}}\left({\frac {m}{3M}}\right)^{2/3}{\frac {a^{2}M^{2}}{100m^{2}}}={\frac {2\pi }{100{\sqrt {G}}}}{\frac {C^{2}}{3^{2/3}}}a^{3/2}M^{5/6}m^{-4/3}$ Bu, kütlesi $m$ olan bir cismin, aşağıdaki koşulları sağlaması halinde belirlenen zaman ölçeği içinde yörüngesini temizleyebileceği anlamına gelir $m\geq {\left[{\frac {2\pi }{100{\sqrt {G}}}}{\frac {C^{2}}{3^{2/3}t_{*}}}a^{3/2}M^{5/6}\right]}^{3/4}={{\left({\frac {2\pi }{100{\sqrt {G}}}}\right)}^{3/4}{\frac {C^{3/2}}{{\sqrt {3}}{t_{*}}^{3/4}}}a^{9/8}M^{5/8}}$ Bu, aşağıdaki gibi yeniden yazılabilir ${\frac {m}{m_{\text{Earth}}}}\geq {{\left({\frac {2\pi }{100{\sqrt {G}}}}\right)}^{3/4}{\frac {C^{3/2}}{{\sqrt {3}}{t_{*}}^{3/4}}}{\left({\frac {a}{a_{\text{Earth}}}}\right)}^{9/8}{\left({\frac {M}{M_{\text{Sun}}}}\right)}^{5/8}{\frac {a_{\text{Earth}}^{9/8}M_{\text{Sun}}^{5/8}}{m_{\text{Earth}}}}}$ Böylece değişkenler güneş kütleleri, Dünya kütleleri ve AU cinsinden mesafeler kullanılacak şekilde değiştirilebilir. ${\frac {M}{M_{\text{Sun}}}}\to {\bar {M}},{\frac {m}{m_{\text{Earth}}}}\to {\bar {m}},$ ve ${\frac {a}{a_{Earth}}}\to {\bar {a}}$ Daha sonra, $t_{*}$ yıldızın ana kol ömrü $t_{\text{MS}}$ olarak eşitlendiğinde, yukarıdaki ifade şu şekilde yeniden yazılabilir $t_{*}\simeq t_{\text{MS}}\propto {\left({\frac {M}{M_{\text{Sun}}}}\right)}^{-5/2}t_{Sun},$ $t_{\text{Sun}}$ Güneş'in anakol ömrü ve değişkenlerde benzer bir değişiklik yaparak yıl cinsinden zaman ${\frac {t_{\text{Sun}}}{P_{\text{Earth}}}}\to {\bar {t}}_{Sun}.$ Bu, daha sonra şu sonucu verir ${\bar {m}}\geq {\left({\frac {2\pi }{100{\sqrt {G}}}}\right)}^{3/4}{\frac {C^{3/2}}{{\sqrt {3}}{{\bar {t}}_{\text{Sun}}}^{3/4}}}{\bar {a}}^{9/8}{\bar {M}}^{5/2}{\frac {a_{\text{Earth}}^{9/8}M_{\text{Sun}}^{5/8}}{m_{\text{Earth}}P_{\text{Earth}}^{3/4}}}$ Bu durumda, yörünge temizleme parametresi cismin kütlesinin yörüngesini temizlemek için gereken minimum kütleye bölünmesiyle elde edilir (bu, yukarıdaki ifadenin sağ tarafıdır) ve basitlik açısından çubuklar çıkarıldığında bu makalede verilen Π ifadesi elde edilir: $\Pi ={\frac {m}{m_{\text{clear}}}}={\frac {m}{a^{9/8}M^{5/2}}}{\left({\frac {100{\sqrt {G}}}{2\pi }}\right)}^{3/4}{\frac {{\sqrt {3}}{t_{\text{Sun}}}^{3/4}}{C^{3/2}}}{\frac {m_{\text{Earth}}P_{\text{Earth}}^{3/4}}{a_{\text{Earth}}^{9/8}M_{\text{Sun}}^{5/8}}}.$ Bu da şu anlama gelir $k={\left({\frac {100{\sqrt {G}}}{2\pi }}\right)}^{3/4}{\frac {{\sqrt {3}}{t_{\text{Sun}}}^{3/4}}{C^{3/2}}}m_{\text{Earth}}P_{\text{Earth}}^{3/4}a_{\text{Earth}}^{-9/8}M_{\text{Sun}}^{-5/8}$ Dünya'nın yörünge periyodu daha sonra $a_{\text{Earth}}$ ve $P_{\text{Earth}}$ ifadesini çıkarmak için kullanılabilir: $P_{\text{Earth}}=2\pi {\sqrt {\frac {{a_{\text{Earth}}}^{3}}{M_{\text{Sun}}G}}},$ bu da şu sonucu verir $k={\left({\frac {100{\cancel {\sqrt {G}}}}{\cancel {2\pi }}}\right)}^{3/4}{\frac {{\sqrt {3}}{t_{\text{Sun}}}^{3/4}}{C^{3/2}}}m_{\text{Earth}}{\left({\cancel {2\pi }}{\sqrt {\frac {\cancel {{a_{\text{Earth}}}^{3}}}{M_{\text{Sun}}{\cancel {G}}}}}\right)}^{3/4}{\cancel {a_{\text{Earth}}^{-9/8}}}M_{\text{Sun}}^{-5/8},$ böylece şu hale gelir $k={\sqrt {3}}C^{-3/2}(100t_{\text{Sun}})^{3/4}{\frac {m_{\text{Earth}}}{M_{\text{Sun}}}}$ Sayıları yerine koyduğumuzda $k$ = 807 elde edilir.
^ Bu değerler, Ceres ve asteroit kuşağı için tahmin edilen $k$ değerine dayanmaktadır: $k$ , 1,53×10⁵ AU^1,5/M_🜨²'ye eşittir, burada AU astronomik birimdir ve M_🜨 Dünya'nın kütlesidir. Buna göre, $Λ$ boyutsuz bir değerdir.

Kaynakça

^ "IAU 2006 General Assembly: Result of the IAU Resolution votes". IAU. 24 Ağustos 2006. 30 Aralık 2009 tarihinde kaynağından arşivlendi. Erişim tarihi: 23 Ekim 2009.
^ ^a ^b ^c ^d ^e ^f Margot, Jean-Luc (15 Ekim 2015). "A Quantitative Criterion for Defining Planets". The Astronomical Journal. 150 (6). ss. 185–191. arXiv:1507.06300 $2. Bibcode:2015AJ....150..185M. doi:10.1088/0004-6256/150/6/185 .
^ ^a ^b ^c ^d Stern, S. Alan; Levison, Harold F. (2002). "Regarding the criteria for planethood and proposed planetary classification schemes" (PDF). Highlights of Astronomy. Cilt 12. ss. 205–213, as presented at the XXIVth General Assembly of the IAU–2000 [Manchester, UK, 7–18 August 2000]. Bibcode:2002HiA....12..205S. doi:10.1017/S1539299600013289 . 23 Eylül 2015 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 16 Eylül 2024.
^ ^a ^b ^c ^d ^e Soter, Steven (16 Ağustos 2006). "What Is a Planet?". The Astronomical Journal. 132 (6). ss. 2513–2519. arXiv:astro-ph/0608359 $2. Bibcode:2006AJ....132.2513S. doi:10.1086/508861.
^ Margot, Jean-Luc; Gladman, Brett; Yang, Tony (1 Temmuz 2024). "Quantitative Criteria for Defining Planets". The Planetary Science Journal. 5 (7). s. 159. arXiv:2407.07590 $2. Bibcode:2024PSJ.....5..159M. doi:10.3847/PSJ/ad55f3 .
^ ^a ^b ^c ^d ^e Kuiper kuşağının kütlesi için Iorio, 2007 25 Ekim 2018 tarihinde Wayback Machine sitesinde arşivlendi. kaynağında bulunan 0,033 Dünya kütlesi tahmini kullanılarak hesaplanmıştır.
^ Bölgede en az 15 Sedna kütlesindeki nesnenin tahmini kullanarak hesaplanmıştır. Tahmin şu çalışmada bulunabilir: Schwamb, Megan E; Brown, Michael E; Rabinowitz, David L (2009). "A Search for Distant Solar System Bodies in the Region of Sedna". The Astrophysical Journal. 694 (1). ss. L45–8. arXiv:0901.4173 $2. Bibcode:2009ApJ...694L..45S. doi:10.1088/0004-637X/694/1/L45.
^ Rincon, Paul (25 Ağustos 2006). "Pluto vote 'hijacked' in revolt". BBC News. 11 Nisan 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 3 Eylül 2006.
^ "Pluto's Planet Title Defender: Q & A With Planetary Scientist Alan Stern". Space.com. 24 Ağustos 2011. 14 Ağustos 2012 tarihinde kaynağından arşivlendi. Erişim tarihi: 8 Mart 2016.