X²
x² şu anlamlara gelebilir:
Matematik
- Kare (cebir), "algebraic square" olarak da bilinen, cebirdeki bir kavram
- Ki-kare dağılımı, teorik bir olasılık dağılımı
x² şu anlamlara gelebilir:
Matematik
Cebir sayılar teorisini, geometriyi ve analizi içine alan geniş bir matematik dalıdır. Temel matematik işlemlerinden, çember ve daire alanları bulmayı kapsayan geniş bir ilgi alanına sahiptir. Cebir, mühendislik ve eczacılık gibi birçok alanda kullanılmaktadır. Kuramsal cebir, ileri matematiğin bir dalı olmakla birlikte sadece uzmanlar tarafından çalışılan bir koldur.

Hârizmî ya da tam künyesiyle Ebû Ca'fer Muhammed bin Mûsâ el-Hârizmî ; matematik, gök bilim, coğrafya ve algoritma alanlarında çalışmış Fars bilim insanı. Hârizmî 780 yılında Harezm bölgesinin Hive şehrinde dünyaya gelmiştir. 850 yılında Bağdat'ta ölmüştür.

Soyut cebir veya soyut matematik, matematiğin bir alanı olup, cebirsel yapılar üzerinde çalışır. Cebirsel yapılar, elemanları üzerinde belirli işlemlerin uygulandığı kümelerdir ve gruplar, halkalar, alanlar, modüller, vektör uzayları, kafesler ve alan üzerindeki cebirler içerir. Soyut cebir terimi, 20. yüzyılın başlarında temel cebirden ayırmak amacıyla türetilmiştir. Soyut cebir ileri matematik için temel hale geldikçe basitçe "cebir" olarak adlandırılırken, "soyut cebir" terimi pedagoji dışında nadiren kullanılır.
Regresyon analizi, iki ya da daha çok nicel değişken arasındaki ilişkiyi ölçmek için kullanılan analiz metodudur. Eğer tek bir değişken kullanılarak analiz yapılıyorsa buna tek değişkenli regresyon, birden çok değişken kullanılıyorsa çok değişkenli regresyon analizi olarak isimlendirilir. Regresyon analizi ile değişkenler arasındaki ilişkinin varlığı, eğer ilişki var ise bunun gücü hakkında bilgi edinilebilir. Regresyon terimi için öz Türkçe olarak bağlanım sözcüğü kullanılması teklif edilmiş ise de Türk ekonometriciler arasında bu kullanım yaygın değildir.

Olasılık kuramı ve istatistik bilim dallarında ki-kare dağılım özellikle çıkarımsal istatistik analizde çok geniş bir pratik kullanım alanı bulmuştur.

Başlangıçta sonsuz küçük hesap veya "sonsuz küçüklerin hesabı" olarak adlandırılan kalkülüs, geometrinin şekillerle çalışması ve cebirin aritmetik işlemlerin genellemelerinin incelenmesi gibi, kalkülüs sürekli değişimin matematiksel çalışmasıdır.
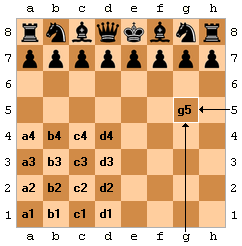
Satranç tahtası, üzerinde 64 kare ile oynanan, kenarları birbirine eşit dört köşe bir alandır. Bu alanda açık ve koyu renkli her birine "kare" denilen kutucuklar vardır. Tahta üzerinde bulunan kareler satranç taşlarının hareket ettikleri "yolları" oluştururlar. Sağa-sola doğru olanlara yatay yol, yukarı aşağı olanlara dikey yol denir. Bu yolların dışında tahtanın üzerinde koyu renkli çapraz karelerden oluşan siyah çapraz yollar, açık renk çapraz karelerden oluşan beyaz çapraz yollar da bulunur. Satranç tahtasında sekiz yatay yol vardır ve cebirle gösterimde bu yollar 1-8 arası rakamlar ile gösterilir. Aynı şekilde tahtanın üzerinde bulunan sekiz adet dikey yol da soldan başlayarak a, b, c, d, e, f, g, h harflerini alır.

Standart sapma, Olasılık kuramı ve istatistik bilim dallarında, bir anakütle, bir örneklem, bir olasılık dağılımı veya bir rassal değişken, veri değerlerinin yayılımının özetlenmesi için kullanılan bir ölçüdür. Matematik notasyonunda genel olarak, bir anakütle veya bir rassal değişken veya bir olasılık dağılımı için standart sapma σ ile ifade edilir; örneklem verileri için standart sapma için ise s veya s'
Bir olasılık dağılımı bir rassal olayın ortaya çıkabilmesi için değerleri ve olasılıkları tanımlar. Değerler olay için mümkün olan tüm sonuçları kapsamalıdır ve olasılıkların toplamı bire eşit olmalıdır. Örneğin, bir rassal olay olarak madeni paranın tek bir defa havaya atılıp yere düşmesi ele alınsın; değerler 'yazı' veya 'tura' veya bunlar isimsel değişken ölçeğinde ifade edilirse 0 (yazı) veya 1 (tura) olur; olasılıklar ise her iki değer için ½ olacaktır. Böylece madeni bir paranın tek bir defa atılma olayı için iki değer ve ilişkili iki olasılık bu rassal olayın olasılık dağılımı olur. Bu dağılım ayrık olasılık dağılımıdır; çünkü sayılabilir şekilde ayrı ayrı sonuçlar ve bunlara bağlı olan pozitif olasılıklar vardır.

Olasılık kuramı ve istatistik bilim kollarında, F-dağılımı bir sürekli olasılık dağılımdır. Bu dağılımı ilk bulan istatistikçiler olan R.A. Fisher veGeorge W. Snedecor adlarına bağlı olarak Snedecor'un F dağılımı veya Fisher-Snedecor dağılımı olarak da anılmaktadir.
Olasılık teorisi ya da ihtimaliyet teorisi rastgele olayların analizi ile ilgilenen bir matematik bilim dalıdır. Olasılık teorisinin ana ögeleri rassal değişkenler, saf rassal süreçler, olaylar olarak sayılabilir. Bunlar ya tek olarak ortaya çıkan veya bir zaman dönemi içinde gelişerek meydana gelen, ilk görünüşü rastgele bir şekilde olan deterministik olmayan olayların veya ölçülebilir miktarların matematiksel soyutlamalarıdır. Bir madeni parayı yazı-tura denemesi için havaya atmak veya bir zarı atmak ile ortaya çıkan sonuç ilk bakışta rastgele bir olay olarak görülebilirse bile eğer birbirini takip eden rastgele olaylar tekrar tekrar ortaya çıkartılırsa incelenebilecek ve tahmin edilebilecek belirli bir istatistiksel seyir takip ettikleri görülecektir. Bu türlü olaylar ve sonuçların seyirlerini betimleyen iki temsilci matematiksel sonuç büyük sayılar yasası ve merkezsel limit teoremidir.
Matematik bilimi içinde moment kavramı fizik bilimi için ortaya çıkartılmış olan moment kavramından geliştirilmiştir. Bir bir reel değişkenin reel-değerli fonksiyon olan f(x)in c değeri etrafında ninci momenti şöyle ifade edilir:

X2 şu anlamlara gelebilir:

Cebirde bir sayının karesi o sayının kendisiyle çarpılması sonucu elde edilen sayıdır. Karesi alınan x sayısı x² biçiminde yazılır.
Olasılık kuramında olay, kendisine bir olasılık değeri atanan sonuç kümesine verilen addır. Örnek uzayın sonlu olması durumunda bu kümenin herhangi bir altkümesi bir olay oluşturmaktadır. Ne var ki, bu yaklaşım örnek uzayın sonsuza uzandığı durumlarda işe yaramamaktadır. Bu nedenle, olasılık uzayı tanımlamalarında örnek uzayın bazı altkümeleri göz önüne alınmaz.
Ki-kare testi veya χ² testi istatistik bilimi içinde bir sıra değişik problemlerde kullanılan bazıları parametrik olmayan sınama ve diğerleri parametrik sınama yöntemidir. Bu çeşit istatistiksel sınamalarda test istatistiği için "örnekleme dağılımı", sıfır hipotez gerçek olursa ki-kare dağılımı gösterir veya sıfır hipotez "asimptotik olarak gerçek" olursa, eğer sıfır hipotez gerçekse ve eğer örnekleme hacmi istenilen kadar yeterli olarak büyük ise bir ki-kare dağılımına çok yakın olarak yaklaşım gösterir.
Pearson ki-kare testi nicel veya nitel değişkenler arasında bağımlılık olup olmadığının, örnek sonuçlarının belirli bir teorik olasılık dağılımına uygun olup olmadığının, iki veya daha fazla örneğin aynı anakütleden gelip gelmediğinin, ikiden fazla anakütle oranının birbirine eşit olup olmadığının ve çeşitli anakütle oranlarının belirli değere eşit olup olmadığının araştırılmasında kullanılır. İstatistik biliminin çıkarımsal istatistik bölümünde ele alınan iki-değişirli parametrik olmayan test analizlerinden olan ve ki-kare dağılımı'nı esas olarak kullanan ki-kare testlerinden en çok kullanılanıdır. İngiliz istatistikçi olan Karl Pearson tarafından 1900'da ortaya çıkartılmıştır.
Bilgisayar bilimi, matematiksel modelleme ve problem çözme yaklaşımlarında köklü bir değişim geçirmektedir. İlk bilgisayar bilimcileri öncelikle ayrık matematik ile ilgilenmişlerdir. Bu dönemde grafikler, ağaçlar ve sonlu sayıda veri seti içeren diziler gibi yapılara odaklanmışlardır. Hızlı kayan noktalı işlemleri "büyük veriler" ile birlikte icra etmeye çalışmışlardır. Üç boyutlu taramanın ve diğer yoğun girdi kaynaklarının gerçeklenmesi modern bilgisayar bilimi pratisyenleri ve mühendisleri tarafından mümkün kılınmıştır. Buna paralel olarak gerçek değere yakın veriyi işlemek ve anlamak için sağlam yöntemler tasarlama ihtiyacı da doğmuştur. Bu ihtiyacın karşılanması için bilgisayar bilimcileri, özellikle ayrık matematik, çok değişkenli hesap, lineer cebir gibi alanlarda bilgi ve tecrübelerini kullanmalıdırlar.
Doğrusal cebirde, tersinir veya regüler matris tersi alınabilen bir kare matristir. 





Matematiksel istatistik, istatistiksel veri toplama tekniklerinin aksine, matematiğin bir dalı olan olasılık teorisinin istatistiğe uygulanmasıdır. Bunun için kullanılan özel matematiksel teknikler arasında matematiksel analiz, doğrusal cebir, stokastik analiz, diferansiyel denklemler ve ölçü teorisi bulunur.