
Bir üçgen düzlemde birbirine doğrusal olmayan üç noktayı birleştiren üç doğru parçasının birleşimidir. Üçgene müselles ve üçbucak da denir.

Dik üçgen, iç açılarından biri 90° olan üçgendir. Çemberde çapı gören çevre açı 90°'dir.

Trigonometri, üçgenlerin açıları ile kenarları arasındaki bağıntıları konu edinen matematik dalı. Trigonometri, sinüs ve kosinüs gibi trigonometrik işlevlerin (fonksiyon) üzerine kurulmuştur ve günümüzde fizik ve mühendislik alanlarında sıkça kullanılmaktadır.

Sinüs teoremi, bir çembersel üçgende bir kenar ve bu kenar karşısındaki açının sinüsleri oranı sabittir. Sinüs, dik açılı üçgenlerde dik olmayan bir açının karşısında kalan dik kenar ile hipotenüsün birbirine oranıdır.

Matematikte sinüs, trigonometrik bir fonksiyon. Sin kısaltmasıyla ifade edilir.

Trigonometrik fonksiyonlar, matematikte bir açının işlevi olarak geçen fonksiyonlardır. Geometride üçgenleri incelerken ve periyodik olarak tekrarlanan olayları incelerken sıklıkla kullanılırlar. Genel olarak bir açısı belirli dik üçgenlerde herhangi iki kenarın oranı olarak belirtilirler, ancak birim çemberdeki belirli doğru parçalarının uzunlukları olarak da tanımlanabilirler. Daha çağdaş tanımlarda sonsuz seriler veya belirli bir türevsel denklemin çözümü olarak geçerler.

Matematikte kutupsal koordinat sistemi veya polar koordinat sistemi, noktaların birer açı ve Kartezyen koordinat sistemindeki orijinin eşdeğeri olup "kutup" olarak bilinen bir merkez noktaya olan uzaklıklar ile tanımlandığı, iki boyutlu bir koordinat sistemidir. Kutupsal koordinat sistemi, matematik, fizik, mühendislik, denizcilik, robot teknolojisi gibi birçok alanda kullanılır. Bu sistem, iki nokta arasındaki ilişkinin açı ve uzaklık ile daha kolay ifade edilebildiği durumlar için özellikle kullanışlıdır. Kartezyen koordinat sisteminde, böyle bir ilişki ancak trigonometrik formüller ile bulunabilir. Kutupsal denklemler, çoğu eğri tipi için en kolay, bazıları içinse yegâne tanımlama yöntemidir.

Tanjant, trigonometrik bir fonksiyondur. "tan" ile ifade edilir.

Hipotenüs, 90 derecelik açının karşısındaki kenardır.

Açıortay, geometride bir açıyı iki eşit açı şeklinde bölen yapıdır. Bir açıya teğet tüm çemberler çizilerek merkezleri birleştirilirse, o açının açıortayı elde edilir. Bu nedenle açıortaylardan açının kollarına indirilen dikmeler, o çemberlerden birinin merkezinden teğetlere inilen yarıçap dikmeleri olacağından, dikmeler birbirine eşit olur. Her iki kolda oluşan üçgenler de birbirine eşit olacağından, dikmelerin açıortay kollarını kestiği noktalar ile açının bulunduğu köşeye olan uzaklıklar eşit olur.

Geometride tetrahedron veya dört yüzlü, dört üçgen yüzden oluşan bir çokyüzlüdür (polihedron), her köşesinde üç üçgen birleşir. Düzgün dört yüzlü dört üçgenin eşkenar olduğu bir dört yüzlüdür ve Platonik cisimlerden biridir. Dörtyüzlü, dört yüzü olan tek konveks çokyüzlüdür. Tetrahedron isminin sıfat hali "tetrahedral"dır.

Brewster açısı, belirli bir polarizasyona sahip ışığın transparan bir dielektrik yüzeyden mükemmel şekilde geçip hiç yansımadığı geliş açısıdır. Bu açıda "polarize olmamış" bir ışık gelirse, yüzeyden yansıyan bu ışık dolayısıyla mükemmel polarizedir. Bu özel geliş açısına İskoç fizikçi Sir David Brewster'dan sonra (1781-1868) kendisinin ismi verilmiştir.

Çemberlerde Thales teoremi, alınan A, B ve C noktalarının bir çember üzerinde ve AC doğrusunun bu çemberin çapı olması durumunda, ABC açısının dik açı olacağını belirten geometri teoremi. Thales teoremi çevre açı kurallarının özel bir hâlidir. Adını Thales'ten alan teorem, genellikle ona atfedilir ancak bazı yerlerde Pisagor'la da ilişkilendirilir.

Birim çember Matematikte, yarıçapı bir birim olan çembere birim çember denir. Çoğunlukla, özellikle trigonometride, Öklid düzlemine göre Kartezyen koordinat sisteminde, merkezi orijin üzerinde (0,0) olan ve yarıçapı bir birim olan çemberdir. n birim çember sıklıkla S1; olarak ifade edilir. Genellikle daha büyük boyutları ise birim küredir. (x, y) birim çember üzerinde bir nokta olduğunda, |x| ve |y|, dik olan ve hipotenüsü bir olan üçgenin diğer kenar uzunluklarıdır. Bu nedenle, Pisagor teoremine göre, x ve y bu denklemi karşılamaktadır.


Geometride, Thales teoremi, A, B ve C, AC çizgisinin bir çap olduğu bir daire üzerinde farklı noktalar ise, ∠ABC açısının bir dik açı olduğunu belirtir. Thales teoremi, çevre açı teoreminin özel bir durumudur ve Öklid'in Elemanlar adlı eserinin üçüncü kitabında 31. önermenin bir parçası olarak bahsedilmiş ve kanıtlanmıştır. Genellikle, teoremin keşif için şükran kurbanı olarak bir öküz sunduğu söylenen Miletli Thales'e atfedilir, ancak bazen Pisagor'a da atfedilir.

Öklid geometrisinde, Batlamyus teoremi, bir kirişler dörtgeninin dört kenarı ile iki köşegeni arasındaki bir ilişkiyi gösteridir. Teorem, Yunan astronom ve matematikçi Batlamyus'un adını almıştır. Batlamyus, teoremi astronomiye uyguladığı trigonometrik bir tablo olan kirişler tablosunu oluşturmaya yardımcı olarak kullandı.
Dış açı teoremi, bir üçgenin bir dış açısının ölçüsünün, uzak iç açılarının ölçülerinden daha büyük olduğunu belirten Ökllid'in Elemanlar'ı Önerme 1.16'dır. Bu, mutlak geometride temel bir sonuçtur çünkü ispatı paralellik postülatına bağlı değildir.
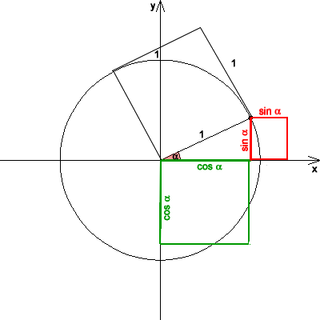
Pisagor trigonometrik özdeşliği, daha basit ifadeyle Pisagor özdeşliği olarak da adlandırılır, Pisagor teoremini trigonometrik fonksiyonlar cinsinden ifade eden bir özdeşliktir. Açıların toplam formülleri ile birlikte, sinüs ve kosinüs fonksiyonları arasındaki temel bağıntılardan biridir. Özdeşlik şu şekildedir:



























