Titreşim

Titreşim bir denge noktası etrafındaki mekanik salınımdır. Bu salınımlar bir sarkaçın hareketi gibi periyodik olabileceği gibi çakıllı bir yolda tekerleğin hareketi gibi rastgele de olabilir.

Titreşim bazen arzu edilir. Örneğin; bir akort çatalının, üflemeli çalgılarda veya mızıkada dilin veya bir hoparlörde koninin hareketi birçok aletin doğru kullanılması için gerekli olan arzu edilir titreşimdir.

Daha sıklıkla, titreşim istenmeyen bir harekettir, çünkü boşa enerji harcar ve istenmeyen ses ve gürültü oluşturur. Örneğin, motorların, elektrik motorlarının ya da herhangi mekanik aracın çalışma esnasındaki hareketi istenmeyen titreşimler üretir. Böyle titreşimler motorlardaki dönen parçaların balanssızlığından, düzensiz sürtünmeden, dişli çarkların hareketinden kaynaklanabilir. Dikkatli tasarımlar genellikle istenmeyen titreşimleri minimize ederler.

Ses ve titreşim çalışmaları birbirleriyle oldukça yakın şekilde bağlantılıdır. Ses, basınç dalgaları, ses telleri gibi yapıları titreştirerek oluşturulur ve basınç dalgaları da kulak zarı gibi yapıların titreşimine sebep olur. Bu yüzden, gürültüyü azaltmaya çalışmak sıklıkla bir titreşimi azaltma problemidir.

Serbest titreşim, bir başlangıç hareketi verilen ve sonra serbestçe salınmaya bırakılan sistemlerde oluşan titreşim türüdür. Bir çocuğu salıncakta sallarken ardından ittirmek ve sonra serbest bırakmak veya bir akord çatalına vurmak ve sonra salınmaya bırakmak bu titreşim türünün örnekleridir. Mekanik sistem, doğal frekansları ve sönümlemelerin bir veya daha fazlasında hareketsiz olana kadar titrer.

Zorlamalı titreşim, mekanik bir sisteme zamanla değişen bir etki (yük, yer değiştirme, hız veya ivme) uygulandığı zamandır. Bu etki, periyodik ve kararlı durum girişi, geçici giriş veya rastgele giriş olabilir. Periyodik girdi, harmonik veya harmonik olmayan bir etki olabilir. Bu tür titreşimlere örnek olarak, bir dengesizlik nedeniyle çamaşır makinesinin sallanması, bir motorun veya bozuk yolun neden olduğu taşıma titreşimi veya depremde binanın titreşimi verilebilir. Doğrusal sistemler için periyodik, harmonik bir girdinin uygulanmasından kaynaklanan kararlı durum titreşim tepkisinin frekansı, uygulanan kuvvetin veya hareketin frekansına eşittir ve tepki büyüklüğü gerçek mekanik sisteme bağlıdır.

Sönümlü titreşim: Titreşimli sistemin enerjisi sürtünme ve diğer dirençler tarafından kademeli olarak dağıtıldığında, titreşimlerin sönümlendiğinden bahsedilir. Titreşimler kademeli olarak azalır veya frekansı veya yoğunluğu değişir veya durur ve sistem denge konumunda kalır. Bu tür titreşime bir örnek, amortisör tarafından sönümlenen araç süspansiyonu'dur.

Titreşim analizinin temelleri, basit kütle-yay-sönüm elemanı modeli incelenerek anlaşılabilir. Aslında bir otomobil gibi karmaşık bir yapı dahi bir basit kütle-yay-sönüm modellerinin toplamı olarak modellenebilir. Kütle-yay-sönüm modeli ise bir basit harmonik osilatör örneğidir ve bu yüzden bunun davranışını tanımlamak için kullanılan matematik RLC devresi gibi diğer basit harmonik osilatörlerdeki ile aynıdır.

Not: Bu sayfada adım adım matematik temellerden bahsedilmemektedir, fakat titreşim analizindeki önemli eşitlikler ve konseptlerden bahsedilecektir. Daha detaylı matematik için sayfanın sonundaki referanslara bakınız.

Kütle-yay-sönüm modelini incelemek için sönümün göz ardı edilebilir olduğunu ve kütleye hiçbir dış kuvvetin etkimediğini varsayıyoruz. (örnek: serbest tireşim)

Yay tarafından kütleye uygulanan kuvvet yayın uzaması “x” ile orantılıdır (Yayın kütlenin ağırlığı dolayısıyla sıkıştırıldığını varsayıyoruz). Orantı sabiti, k, yayın direngenliğidir ve birimi kuvvet/uzama cinsindendir. (Örneğin: lbf/in veya N/m)

${\displaystyle F_{s}=-kx\!}$

Kütle tarafından üretilen kuvvet ise Newton’un ikinci hareket kanununda verilen kütlenin ivmesiyle orantılıdır:

${\displaystyle \Sigma \ F=ma=m{\ddot {x}}=m{\frac {d^{2}x}{dt^{2}}}}$

Kütle üzerindeki kuvvetleri toplayıp aşağıdaki adi diferansiyel denkleme ulaşırız:

${\displaystyle m{\ddot {x}}+kx=0.}$

Eğer sistemi, yayı “A” çekerek titreşime başlattığımızı ve sonra serbest bıraktığımızı varsayarsak, kütlenin hareketini tanımlayan yukarıdaki denklemin çözümü şöyle olur:

${\displaystyle x(t)=A\cos(2\pi f_{n}t)\!}$

Bu çözüm şu anlamdadır: kütle “A” genliğinde ve ${\displaystyle f_{n}}$ frekansında salınmaktadır, burada ${\displaystyle f_{n}}$ titreşim analizindeki en önemli değerlerden biridir ve sönümsüz “doğal frekans” olarak adlandırılır.

${\displaystyle f_{n}}$ basit kütle-yay sistemi için aşağıdaki gibi tanımlanır:

${\displaystyle f_{n}={1 \over {2\pi }}{\sqrt {k \over m}}\!}$

Not: Açısal frekans ${\displaystyle \omega }$ (${\displaystyle \omega =2\pi f}$) (birimi rad/sn) sıklıkla denklemlerde kullanılır çünkü denklemleri kolaylaştırır, fakat sistemin frekansından bahsederken standart frekansa(birimi Hz veya devir/sn) dönüştürülür.

Eğer sistemin kütlesini ve yay sabitini biliyorsanız, sisteme bir ilk hareket verildiğinde hangi frekansta titreyeceğini yukarıdaki formülü kullanarak bulabilirsiniz. Titreyen her sistem, tahrik edildiğinde titreşeceği bir veya daha fazla doğal frekansa sahiptir. Genel olarak bu basit ilişki daha kompleks bir sisteme bir kütle veya direngenlik eklediğimizde ne olduğunu açıklar. Örneğin, yukarıdaki formül bir arabanın veya bir kamyonun tamamıyla yüklü olduğunda neden daha yumuşak hissettirdiğini açıklar; çünkü kütle artmıştır ve bu yüzden sistemin doğal frekansı düşmüştür.

Bu formüller sistemin son hareketini tanımlamakla beraber sistemin neden salındığını açıklamazlar. Bu salınım(osilasyon) enerjinin korunumundan kaynaklanmaktadır. Yukarıdaki örnekteki yayı “A” kadar uzattık ve böylece yayda bir potansiyel enerji (${\displaystyle {\tfrac {1}{2}}kx^{2}}$) depoladık. Serbest bıraktığımızda ise yay uzatılmamış durumuna dönmek ister ve bu yüzden kütleyi ivmelendirir. Yayın uzatılmamış ilk haline döndüğü nokta artık depolanmış enerjiye sahip değildir fakat kütle maksimum hızına ulaşmıştır ve bu yüzden tüm enerji kinetik enerjiye dönmüştür (${\displaystyle {\tfrac {1}{2}}mv^{2}}$). Ardından kütle ivmesini kaybetmeye başlar çünkü şimdi yayı sıkıştırıyor ve kinetik enerjisini potansiyel enerjiye dönüştürüyordur. Kütledeki kinetik enerjinin yaydaki potansiyel enerjiye ve yaydaki potansiyel enerjinin kütledeki kinetik enerjiye dönüşümü salınıma sebep olmaktadır.

Basit modelimize göre kütle sonsuza kadar aynı genlikte salınacaktır, gerçek sistemde daima sönüm denen enerjiyi harcayan ve en sonunda sistemin durmasına neden olan etkiler vardır.

Şimdi sisteme kütlenin hızıyla orantılı olarak kuvvet üreten viskoz bir sönümleyici ekliyoruz.Sönümleme viskoz olarak adlandırılmaktadır çünkü bir akışkanın içindeki bir objeyi modellemektedir. Orantı sabiti “c” sönüm katsayısı olarak adlandırılır ve kuvvet/hız birimindedir (lbf s/ in veya N s/m).

${\displaystyle F_{d}=-cv=-c{\dot {x}}=-c{\frac {dx}{dt}}\!}$

Kütle üzerindeki kuvvetleri toplayarak aşağıdaki adi diferansiyel denlemi elde ederiz:

${\displaystyle m{\ddot {x}}+{c}{\dot {x}}+{k}x=0.}$

Bu denklemin çözümü sönümün miktarına bağlıdır. Eğer sönüm yeterince küçükse sistem titreşecek fakat zaman geçtikçe titremesi sona erecektir. Bu durumda sistem az sönümlü olarak ifade edilir—titreşim analizinin en çok ilgi çeken kısmıdır. Eğer sönümü sistemin artık salınmadığı noktaya kadar arttırırsak kritik sönüme ulaşmış oluruz(eğer sönümü kritik sönümün üzerine de çıkarırsak sistem aşırı sönümlü sistem olarak adlandırılır). Kütle yay sönüm modelinde kritik sönüm için sönüm katsayısının ulaşması gereken değer şudur:

${\displaystyle c_{c}=2{\sqrt {km}}}$

Sistemdeki sönümü tanımlamak için sönüm oranı(sönüm faktörü ve % kritik sönüm de denir) denen bir oran kullanılır. Bu oran sistemdeki gerçek sönümün, kritik sönüme ulaşması için gereken sönüme oranıdır.Kütle yay sönüm modeli için sönüm oranı (${\displaystyle \zeta }$) formülü ise şöyledir:

${\displaystyle \zeta ={c \over 2{\sqrt {km}}}.}$

Örneğin; metal yapılar(uçak gövdeleri, motor krank milleri gibi) 0.05 den daha küçük sönümleme faktörlerine sahipken, otomotiv süspansiyonları 0.2-0.3 aralığındadır.

Az sönümlü kütle yay sönüm sistemi için çözüm aşağıdaki gibidir:

${\displaystyle x(t)=Xe^{-\zeta \omega _{n}t}\cos({{\sqrt {1-\zeta ^{2}}}\omega _{n}t-\phi }),\ \ \omega _{n}=2\pi f_{n}}$

Başlangıç genliği “X” ve faz farkı ${\displaystyle \phi }$ yayın ne kadar sıkıştırıldığına göre değişir. Bu değerlerin formülleri referanslarda bulunabilir.

Bu çözümde fark edilmesi gereken önemli nokta eksponansiyel terim ve kosinüs fonksiyonudur. Eksponansiyel terim sis temin ne kadar hızlı sönümleceğini belirleyen terimdir-sönüm oranı büyüdükçe sistem daha hızlı sönümlenir. Koisinüs fonksiyonu ise çözümün salınım yapan kısmıdır ve salınımın frekansı sönümsüz durumdan farklıdır.

Bu durumdaki frekansa sönümlü doğal frekans, ${\displaystyle f_{d}}$, denir ve aşağıdaki formüle göre sönümsüz doğal frekansla ilişkilidir:

${\displaystyle f_{d}={\sqrt {1-\zeta ^{2}}}f_{n}}$

Sönümlü doğal frekans sönümsüz doğal frekanstan daha düşüktür, fakat birçok pratik durumda sönüm oranı göreceli olarak küçüktür ve bu yüzden aradaki fark göz ardı edilebilir. Bu yüzden sönümlü ve sönümsüz tanımlamalar, doğal frekanstan bahsedildiğinde, büyütülmüş olur. (Örneğin: 0.1 lik sönüm oranında; sönümlü doğal frekans sönümsüz doğal frekanstan %1 küçüktür.)

Yandaki çizimler 0.1 ve 0.3 lük sönüm oranlarının zaman geçtikçe sistemin sönümlenmesini nasıl etkilediğini gösterir. Pratikte sıklıkla yapılan ise bir darbeden sonra (örneğin; bir çekiçle vurduktan sonra) deneysel olarak serbest titreşimi ölçmektir ve bundan sonra salınım oranını ölçerek sistemin doğal frekansı hesaplanır ve düşüş oranı ölçülerek sönüm oranı bulunur. Doğal frekans ve sönüm oranı sadece serbest titreşimde önemli değildir. Aynı zamanda sistemin zorlama altındaki titreşiminde nasıl davranacağını da belirlerler.

Bu bölümde kütle yay sönüm modeline formülü aşağıdaki gibi olan, harmonik değişen bir kuvvet eklediğimizde modelimizin nasıl davranacağına bakacağız. Böyle bir kuvvet örneğin dönmede dengesizlikten kaynaklanabilir.

${\displaystyle F=F_{0}\cos {(2\pi ft)}\!}$

Eğer yine kütle üzerindeki kuvvetleri toplarsak, aşağıdaki adi diferansiyel denklemleri elde ederiz:

${\displaystyle m{\ddot {x}}+{c}{\dot {x}}+{k}x=F_{0}\cos {(2\pi ft)}}$

Bu problemin kararlı durum çözümü şu şekilde yazılabilir;

${\displaystyle x(t)=X\cos {(2\pi ft-\phi )}\!}$

Sonuç, kütlenin uygulanan kuvvetle aynı frekansta, f, salınacağını fakat arada bir faz farkı ${\displaystyle \phi }$ olacağını gösterir.

Titreşimin genliği ”X” ise aşağıdaki formülde olduğu gibi tanımlanır:

${\displaystyle X={F_{0} \over k}{1 \over {\sqrt {(1-r^{2})^{2}+(2\zeta r)^{2}}}}}$

Burada “r” harmonik kuvvetin frekansının sönümsüz kütle-yay-sönüm modelinin doğal frekansı olarak tanımlanır.

${\displaystyle r={\frac {f}{f_{n}}}}$

Faz farkı, ${\displaystyle \phi }$ ise aşağıdaki formülle tanımlanır:

${\displaystyle \phi =\arctan {\left({\frac {2\zeta r}{1-r^{2}}}\right)}}$

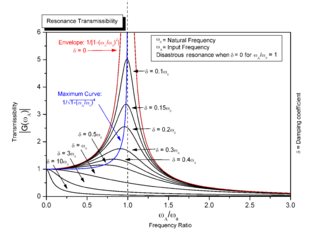
Bu fonksiyonların çizimi, sistemin frekans cevabı denir, zorlamalı titreşmin en önemli özelliklerinden birini gösterir. Zorlama frekansının doğal frekansla hemen hemen aynı olduğu(${\displaystyle r\approx 1}$) çok az sönümlü sistemlerde titreşimin genliği çok yüksek olabilir. Bu olgu rezonans-mekanik rezonans olarak adlandırılır. (Böyle bir durumda sistemin doğal frekansı sıklıkla rezonans frekansı olarak adlandırılır)

Eğer rezonans mekanik bir sistemde meydana gelirse çok zararlı olabilir—sistemde nihai bir bozulmaya sebep olabilir. Sonuç olarak titreşim analizinin en önemli sebeplerinden biri rezonansın ne zaman meydana geleceğini tahmin etmek ve gerçekleşmesini önlemek için ne gibi önlemlerin alınacağına karar vermektir. Genlik çizimlerinde görüldüğü gibi, sönüm eklemek titreşimin genliğini önemli derecede azaltır. Aynı zamanda genlik, sistemin kütlesi veya direngenliği değiştirilerek doğal frekansın zorlama frekansından uzaklaştırılmasıyla da düşürülebilir. Eğer sistem değiştirilemiyorsa, belki zorlama frekansı değiştirilebilir (örneğin kuvvete sebep olan makinenin dönme hızını değiştirerek).

Aşağıdakiler ise zorlamalı titreşimin frekans cevabı çizimleri ile ilgili diğer noktalardır:

• Belirli bir frekans oranında, titreşimin genliği, “X”, doğrudan zorlamanın genliği${\displaystyle F_{0}}$ ile orantılıdır (örneğin kuvveti ikiye katlarsanız titreşimde ikiye katlanır).
• Çok az ya da sıfır sönümde, titreşim zorlama ile aynı fazdadır ve r<1 dir ve eğer 180 dereceli faz farkı mevcutsa frekans oranı r>1 dir.
• r 1’den çok küçükse(r<<1) genlik sadece statik kuvvet ${\displaystyle F_{0}}$ altındaki yayın uzamasıdır.Bu uzama statik uzama ${\displaystyle \delta _{st}}$ olarak adlandırılır.Bu yüzden r<<1 olduğunda sönüm ve kütlenin etkileri minimumdur.
• r>>1 iken titreşimin genliği statik uzamadan ${\displaystyle \delta _{st}}$ daha azdır.Bu bölgede kütle tarafından üretilen kuvvet(F=m.a) hakimdir, çünkü kütlenin maruz kaldığı ivme frekans arttıkça artar.Bu bölgede yaydaki uzama, X, azaldığından, yay tarafından zemine iletilen kuvvet(F=k.x) azalır.Böylece kütle-yay-sönüm sistemi harmonik kuvveti zeminden izole eder—buna titreşim izolasyonu denir.İlginç olarak r>>1 olduğunda daha fazla sönüm titreşim izolasyonunun etkisini azaltır çünkü sönüm kuvveti(F=c.V) de zemine transfer edilmektedir.

Eğer kütle ve yayı enerji depolama elemanları olarak görürseniz rezonansı anlamak çok kolaydır—kütle kinetik enerji depolarken yay ise potansiyel enerji depolar. Daha önce de bahsedildiği gibi, kütle ve yay üzerinde hiçbir kuvvet yoktur, onlar enerjilerini doğal frekansa eşit oranda bir ileri bir geri dönüştürürler. Diğer bir deyişle eğer enerji verimli bir şekilde kütle ve yayın içerisine pompalansaydı enerji kaynağının doğal frekansa eşit oranda beslenmesi gerekirdi. Bir kütle ve yaya bir kuvvet uygulamak bir çocuğu salıncakta sallamaya benzer, eğer daha yükseğe sallamak istiyorsanız doğru zamanda ittirmek zorundasınız. Salıncak örneğinde olduğu gibi daha büyük bir hareket elde etmek için uygulanan kuvvetin illaki çok yüksek olması gerekmemektedir. Bu itmeler sadece enerjinin sistemin içine eklenmesini sağlar.

Sönüm ise enerji depolamak yerine enerjiyi harcar.Sönüm kuvveti hızla orantılı olduğundan, hareket büyüdükçe enerji daha fazla sönümlenir. Böylece sönüm elemanı tarafından sönümlenen enerji ile kuvvet tarafından beslenen enerjinin eşit olduğu bir noktaya ulaşılır.Bu noktada sistem kendi maksimum genliğine ulaşır ve uygulanan kuvvet aynı kaldığı sürece bu genlikte titremeye devam eder.Eğer hiç sönüm yoksa, enerji yutacak hiçbir şey yoktur ve böylece hareket teorik olarak sonsuza gider.

Geçmiş bölümde modelimize sadece basit harmonik bir kuvvet uygulanmıştı, fakat bu iki güçlü matematiksel araç kullanılarak epeyce genişletebilinir. Bunlardan birincisi bir sinyalin zaman fonksiyonunu alıp frekansın bir fonksiyonu olarak harmonik bileşenlerine ayıran Fourier analizidir. Örneğin kütle yay sönüm modelimize şu şekilde tekrar eden bir kuvvet uygulayalım—0.5 sn liğine 1N luk bir kuvvet ve ardından 0.5 saniyeliğine hiç kuvvet uygulamayalım. Bu çeşit kuvvet 1 Hz lik kare dalga şekline sahiptir.

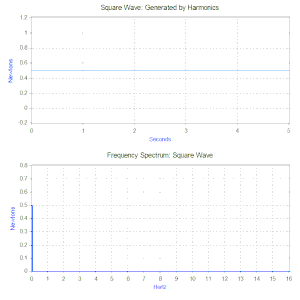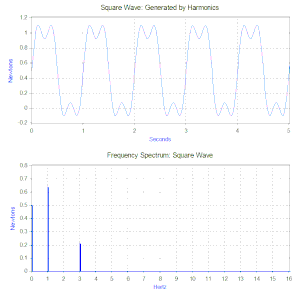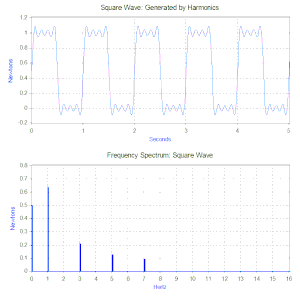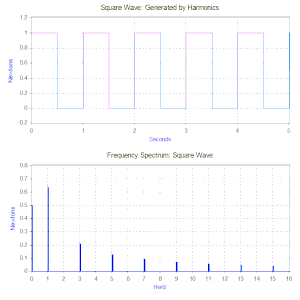
Kare dalganın fourier dönüşümü kare dalgayı oluşturan harmoniklerinin genliklerini gösteren bir frekans spektrumu oluşturur(Aynı zamanda faz farkı da oluşur ancak genellikle bununla daha az ilgilenilir ve bu yüzden sıklıkla da çizilmez). Fourier dönüşümü aynı zamanda geçici (Örneğin: darbeler) veya karışık fonksiyonlar gibi periyodik olmayan fonksiyonların incelenmesinde de kullanılabilir. Modern bilgisayarların avantajlarını kullandığımız günümüzde Fourier dönüşümü daima Hızlı Fourier Dönüşümü(FFT) denen, bir pencere fonksiyonunun kombinasyonu olan bir algoritma kullanılarak bilgisayar ile uygulanır.

Kare dalga kuvvet durumuna döndüğümüzde, birinci öğe 0.5 N’luk sabit bir kuvvettir ve frekans spektrumunda “0” Hz’lik bir değerle temsil edilir. Sonraki öğe ise 1 Hz’lik ve 0.64 genliğinde bir sinüs dalgasıdır. Bu 1 Hz’deki çizgiyle gösterilmiştir. Takip eden öğeler alakasız frekanslardadır ve mükemmel kare dalgalar üretmek için sonsuz sayıda sinüs dalgası içerir. Böylece Fourier dönüşümü bize kuvvetimizi daha kompleks kuvvetler (örneğin kare dalga) yerine uygulanan sinüzoidal kuvvetlerin bir toplamı olarak anlamamızı sağlar.

Geçen bölümde tek bir harmonik kuvvet için titreşim çözümü verilmişti fakat Fourier dönüşümü genellikle çoklu harmonik kuvvetlerde uygulanır. İkinci matematik aracımız ise Süperpozisyon prensibidir. Bu prensip, eğer sistem lineerse kuvvetlerin çözümlerinin toplanmasına izin verir. Kütle-yay-sönüm modelinde eğer yay kuvveti deplasmanla ve sönümde ilgilenilen hareket menzilinde hızla orantılıysa sistem lineerdir. Böylece, kare dalgalı problemin çözümü kare dalganın frekans spektrumunda bulunan harmonik fonksiyonlardan tahmin edilen her bir titreşimin toplanmasıdır.

Bir titreşim probleminin çözümünü bir girdi/çıktı ilişkisi olarak görebiliriz—burada kuvvet girdi titreşim ise çıktıdır. Eğer kuvveti ve titreşimi frekans tabanında gösterirsek(genlik ve faz) aşağıdaki ilişkiyi yazabiliriz:

${\displaystyle X(\omega )=H(\omega )*F(\omega )\ \ or\ \ H(\omega )={X(\omega ) \over F(\omega )}}$

${\displaystyle H(\omega )}$ frekans cevabı fonksiyonu olarak adlandırılır (aynı zamanda transfer fonksiyonu olarak da adlandırılır fakat teknik olarak çok doğru değildir) ve hem genlik hem de faz bileşenlerini (eğer kompleks sayı olarak gösterilirse reel ve sanal bileşenler) içerir. Frekans cevabı fonksiyonunun (FRF-Frequency Response Function) genliği daha önce kütle-yay-sönüm modeli için gösterilmişti.

${\displaystyle |H(\omega )|=\left|{X(\omega ) \over F(\omega )}\right|={1 \over k}{1 \over {\sqrt {(1-r^{2})^{2}+(2\zeta r)^{2}}}},\ \ where\ \ r={\frac {f}{f_{n}}}={\frac {\omega }{\omega _{n}}}}$

FRF’nin fazı da aynı zamanda daha önce aşağıdaki gibi gösterilmişti:

${\displaystyle \angle H(\omega )=\arctan {\left({\frac {2\zeta r}{1-r^{2}}}\right)}}$

Örneğin; kütlesi 1 kg, yay direngenliği1.93 N/mm ve sönüm oranı 0.1 olan bir kütle yay sönüm sisteminin FRF’sini hesaplayalım. Bu sistem için verilen kütle ve yay değerleri 7 Hz lik bir doğal frekans verir. Eğer önceki 1 Hz lik kare dalgayı sisteme uygularsak kütlenin tahmin edilen titreşimini hesaplayabiliriz. Şekil nihai titreşimi göstermetedir. Bu örnekte kare dalganın dördüncü harmoniği 7 Hz e denk düşer. Girdi kuvveti görece düşük 7 Hz lik bir harmoniğe sahipken kütle yay sönüm yüksek bir 7 Hz lik titreşim oluşturur. Bu örnek çıkış fonksiyonunun hem zorlama fonksiyonuna hem de kuvvetin uygulandığı sisteme bağlı olduğunu açığa çıkarır.

Şekil aynı zamanda çıkış fonksiyonunun zaman tabanı gösterimini de içerir. Bu ters bir Fourier analizi kullanılarak frekans tabanından zaman tabanına geçerek yapılmıştır. Uygulamada, bu pek yapılmaz çünkü frekans spektrumu bütün gerekli bilgileri sağlar.

Frekans cevabı fonksiyonunun(FRF) illaki sistemin kütlesi, direngenliği ve sönümü bilinerek hesaplanması gerekmez; deneysel olarak da ölçülebilir. Örneğin; eğer bilinen bir kuvvet uygularsak ve frekansı tararsak ve ardından çıkış fonksiyonunu ölçersek frekans cevap fonksiyonunu hesaplayabilir ve böylece sistemi karakterize etmiş oluruz. Bu teknik bir yapının titreşim karakteristiklerini belirlemek için deneysel modal analiz alanında kullanılır.

Vibrasyon motorları çeşitli enerji biçimlerinden hareket enerjisi elde etmek ve bu enerjiyi salınım enerjisine çevirmek maksadıyla oluşturulan mekanizmaların genel ismidir. Çeşitli sektörlerde özellikle elektrikli vibrasyon motorları için vibratör ve vibro-motor isimleri de kullanılmaktadır.

• Rao, Singiresu, Mechanical Vibrations, Addison Wesley, 1990, ISBN 0-201-50156-2
• Thompson, W. T., Theory of Vibrations, Nelson Thornes Ltd, 1996, ISBN 0-412-78390-8
• Hartog, Den, Mechanical Vibrations, Dover Publications, 1985, ISBN 0-486-64785-4

Vikisözlük'te Titreşim ile ilgili tanım bulabilirsiniz.

Wikimedia Commons'ta Titreşim ile ilgili ortam dosyaları bulunmaktadır.

• Thermotron Industries, Fundamentals of Electrodynamic Vibration Testing Handbook
• Nelson Publishing, Evaluation Engineering Magazine