
Pisagor teoremi veya Pisagor bağıntısı, Öklid geometrisinde üçgenin kenarları arasındaki temel ilişkiyi kuran ilk teoremlerden biridir. Teoreme gerçek hayattan örnek olarak telli çalgıları gösterilebilir; 'telin uzunluğu arttıkça titreşim artar' prensibine dayanır. Pisagor'un denklemi olarak da isimlendirilen bu teorem, a, b ve c kenarlarının arasındaki ilişkiyi şu şekilde açıklar:


Rubik Küpü, Zekâ Küpü ya da Sabır Küpü; 1974 yılında Macar heykeltıraş ve mimar Ernő Rubik tarafından icat edilen mekanik bulmacadır. Hareketli yüzeylerden oluşan ve çoğunlukla plastikten yapılmış bir küp olan Rubik Küpü, başlıca dört şekilde piyasaya sürülmüştür: 2×2×2'lik Mini Rubik Küpü, 3×3×3'lük standart küp, 4×4×4'lük Rubik'in İntikamı ve 5×5×5'lik Profesörün Küpü. 6×6×6 ve 7×7×7'lik küpler de hâlihazırda üretilmektedir. Standart olan ve 6 yüzeye sahip bir rubik küp, toplam 27 parçadan oluşur.

Barkod, çubuk kod ya da çizgi im, verilerin görsel özellikli makinelerin okuyabilmesi için çeşitli kodlama yöntemleriyle sunulmasıdır.

Matematikte bir döşeme, aralarında boşluk bırakmadan veya örtüşmeden bir düzlemi kaplayan düzlemsel şekiller kümesidir. Bu kavram daha yüksek boyutlar için de genellenebilir, bu genişletilmiş anlamı için döşeme yerine tesselasyon terimi kullanılır. Tesselasyon M. C. Escher'in eserlerinde sıkça görülebilir. Tesselasyona sanat tarihi boyunca, antik mimariden modern sanata kadar rastlanabilir.

Geometride tetrahedron veya dört yüzlü, dört üçgen yüzden oluşan bir çokyüzlüdür (polihedron), her köşesinde üç üçgen birleşir. Düzgün dört yüzlü dört üçgenin eşkenar olduğu bir dört yüzlüdür ve Platonik cisimlerden biridir. Dörtyüzlü, dört yüzü olan tek konveks çokyüzlüdür. Tetrahedron isminin sıfat hali "tetrahedral"dır.

Geometride, iki doğru veya iki düzlem kesiştiklerinde oluşturdukları komşu açılar birbirine eşitse dik olarak kabul edilir.

Kristalografi olarak, kübik kristal sistemi, birim hücresi bir küp biçiminde olan kristal sistemidir. Bu kristal ve mineraller bulunan en yaygın ve basit şekillerden biridir. Bu kristallerin üç ana çeşidi vardır:
- Basit Kübik Kafes (cP)
- Hacim Merkezli Kübik Kafes,
- Yüzey Merkezli Kübik Kafes

Kenar ya da ayrıt, düzlemsel yüzeylerin birbirine bitiştikleri çizgi. Bir çokgenin iki köşesini birleştiren doğru parçası.
Aşağıdaki iyi-tanımlanmış bazı matematiksel şekillerin listesidir.

Doğrusal cebirde, kare matris, satır ve sütun sayıları eşit olan bir matrisdir. n ye n lik bir matris, boyutu n olan bir kare matris olarak bilinir. Aynı boyuta sahip herhangi iki matriste, toplama ve çarpma işlemleri yapılabilir.

Geometride, Thales teoremi, A, B ve C, AC çizgisinin bir çap olduğu bir daire üzerinde farklı noktalar ise, ∠ABC açısının bir dik açı olduğunu belirtir. Thales teoremi, çevre açı teoreminin özel bir durumudur ve Öklid'in Elemanlar adlı eserinin üçüncü kitabında 31. önermenin bir parçası olarak bahsedilmiş ve kanıtlanmıştır. Genellikle, teoremin keşif için şükran kurbanı olarak bir öküz sunduğu söylenen Miletli Thales'e atfedilir, ancak bazen Pisagor'a da atfedilir.
Beş boyutlu uzay fikri, matematikte sıklıkla ortaya çıkan soyut bir terim.
Kübik atom modeli Elektronların kutupsuz atomlar veya moleküller olarak bir küpün 8 köşesine sıralandığı bir atom modelidir. Bu teori 1902'de Gilbert Newton Lewis tarafından geliştirilmiştir.1916'da "The Atom and Molecule" (Atom ve Molekül" adlı makalede yayınlanmıştır ve Değerlik olgusunu açıklamak için kullanılmıştır. Lewis'in teorisi Abegg'in kuralına dayanıyordu. Irving Langmuir bunu 1919'da geliştirerek "cubical octet atom" modeli haline getirmiştir. Aşağıdaki resim, Periyodik tablonun ikinci satırındaki elementler için yapısal gösterimleri göstermektedir.

Birim küp, kenarları 1 birim uzunluğunda olan küptür. Üç boyutlu birim kübün hacmi 1 birim küp, toplam yüzey alanı ise 6 birim karedir.
Dinostratus, Menaechmus'un kardeşi olan Yunan matematikçi ve geometriciydi. Daireyi kareleştirme problemini çözmek için kuadratrisi kullanmasıyla tanınır.
Thales teoremi veya temel orantı teoremi olarak da bilinen kesişme teoremi, kesişen iki çizginin bir çift paralelle kesilmesi durumunda oluşturulan çeşitli çizgi parçalarının oranları hakkındaki temel geometride önemli bir teoremdir. Benzer üçgenlerdeki oranlarla ilgili teoreme eşdeğerdir. Geleneksel olarak Yunan matematikçi Thales'e atfedilir.

Gnomon teoremi, bir gnomon'da meydana gelen belirli paralelkenarların eşit büyüklükte alanlara sahip olduğunu belirtir. Gnomon, geometride benzer bir paralelkenarı daha büyük bir paralelkenarın bir köşesinden çıkararak oluşturulan bir düzlem şeklidir; veya daha genel olarak, belirli bir şekle eklendiğinde, aynı şekle sahip daha büyük bir şekil oluşturan bir şekildir.
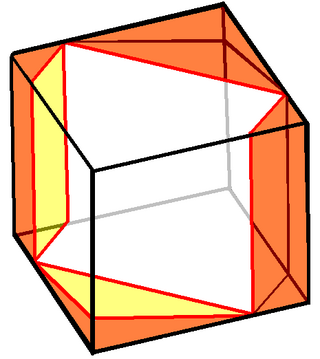
Prince Rupert'ın küpü, geometride, bir birim küp içine tüm boyunca kesilmiş bir delikten geçebilen en büyük küptür. Yani kenarları 1 birim uzunlukta olan bir küpten, küpü iki parçaya bölmeden geçebilir. Yan uzunluğu, içinden geçtiği birim küpünkinden yaklaşık %6 daha büyüktür. Tamamen bir birim küp içinde yer alan en büyük kareyi bulma sorunu ile çok yakından ilişkilidir ve aynı çözüme sahiptir.

Dört boyutlu uzay (4B), üç boyutlu veya 3 boyutlu uzay kavramının matematiksel bir uzantısıdır. Üç boyutlu uzay, gündelik yaşamdaki nesnelerin boyutlarını veya konumlarını tanımlamak için yalnızca boyut adı verilen üç sayıya ihtiyaç duyulduğu gözleminin mümkün olan en basit soyutlamasıdır. Örneğin, dikdörtgen bir kutunun hacmi, uzunluğu, genişliği ve yüksekliği ölçülerek ve çarpılarak bulunur.





















