Temas açısı

Temas açısı , bir damlanın sıvı-buhar sınırı ve katı yüzey arasında buluşan açıdır. Young denklemi ile katı bir yüzeyin bir sıvı tarafından ıslatılabilirliğini ölçmektedir. Belirli bir sıcaklık ve basınçta belirli bir katı, sıvı ve buhar sistemi benzersiz bir denge temas açısına sahiptir. Bununla birlikte, uygulamada, ilerleyen (maksimal) temas açısından çekik (minimal) temas açısına kadar değişen dinamik bir temas açısı histerezisi fenomeni sıklıkla gözlenmektedir.[1] Termodinamik denge teması bu değerler dahilindedir ve bunlardan hesaplanabilir. Termodinamik denge temas açısı, sıvı, katı ve buhar moleküler etkileşiminin göreceli gücünü yansıtır.
Termodinamik

Sıvı-buhar sınırıı şekli Young-Dupré denklemi ile belirlenir; temas açısı, Young denklemi yoluyla bir sınır koşulunun rolünü oynar.
Temasın teorik açıklaması, üç faz arasındaki termodinamik dengenin dikkate alınmasından kaynaklanır: sıvı faz (L), katı faz (S) ve gaz veya buhar fazı (G) (ortam atmosferinin bir karışımı olabilir) ve sıvı buharın denge konsantrasyonu). ("Gaz halinde" faz, başka bir karışmayan sıvı faz ile değiştirilebilir.) Katı-buhar arayüzey enerjisi, , katı-sıvı arayüzey enerjisi ve sıvı-buhar arayüzey enerjisini (yani yüzey gerilimi ) , sonra denge temas açısı bu miktarlardan Young denklemi ile belirlenir :
Temas açısı ayrıca Young-Dupré denklemi ile yapışma çalışması ile de ilgili olabilir:
nerede G ortamındayken birim alan başına katı - sıvı yapışma enerjisidir.
Modifiye Young denklemi
İlk olarak 1805’ de Thomas Young, ıslanmanın, bir sıvının bir yüzey üzerine yayılmasının olup olmayacağını belirleyen kohezyon ve adhezyon kuvvetleri arasındaki etkileşimi tanımlamıştır.[2] Bir yüzyıl sonra Gibbs[3] temas açısının hacimsel bağımlılığını açıklamak için Young denkleminde bir değişiklik önerdi. Gibbs, üç fazlı sınırda hareket eden ve katı-sıvı-gaz faz arayüzünün birleştiği yerde fazla enerjiyi açıklayan bir çizgi geriliminin varlığını varsaydı ve şöyle verildi:
nerede κ [N] hat gerilimi ve a[m] olduğu damlanın yarıçapıdır. Deneysel veriler temas açısının kosinüsü ile ters çizgi yarıçapı arasındaki afin bir ilişkiyi doğrulasa da, doğru sign işaretini hesaba katmaz ve değerini birkaç büyüklük sırasına göre fazla tahmin eder.
Hat gerilimi ve Laplace basıncı hesaplanırken temas açısı tahmini
Atomik kuvvet mikroskopisi, konfokal mikroskopi ve taramalı elektron mikroskobu gibi ölçüm tekniklerindeki gelişmelerle, araştırmacılar daha küçük ölçeklerde damlacıklar üretebildiler ve görüntü elde edebildiler. Damlacık boyutundaki azalma ile ıslanma ile ilgili yeni deneysel gözlemler geldi. Bu gözlemler, değiştirilmiş Young denkleminin mikro-nano ölçeklerde olmadığını doğruladı. Jasper [4][5] bir V dahil Serbest enerjinin varyasyonundaki V dP terimi, bu küçük ölçeklerde temas açısı problemini çözmenin anahtarı olabilir. Serbest enerjideki varyasyonun dengede sıfır olduğu göz önüne alındığında:
Serbest sıvı-buhar sınırındaki basınçtaki değişim, ortalama Gauss eğriliği ile orantılı olan Laplace basıncından kaynaklanmaktadır. Hem dışbükey hem de içbükey yüzeyler için yukarıdaki denklemin çözülmesi aşağıdakileri sağlar:[4]
nerede , ve .
Bu denklem, temas açısını, kütle termodinamiğine sesil damlacıkların geometrik bir özelliğini, üç faz temas sınırındaki enerjiyi ve damlacığın ortalama eğriliğini ilişkilendirir. Düz bir yüzey üzerinde sapsız damlacık için özel durum :
Yukarıdaki denklemde, ilk iki terim değiştirilmiş Young denklemidir, üçüncü terim ise Laplace basıncından kaynaklanmaktadır. Bu doğrusal olmayan denklem sign işaretini ve büyüklüğünü, çok küçük ölçeklerde temas açısının düzleşmesini ve temas açısı histerezisini doğru olarak tahmin eder.
Temas açısı histerezisi
Belirli bir substrat-sıvı-buhar kombinasyonu pratikte sürekli bir temas açısı değerleri aralığı verir. Maksimum temas açısı ilerleyen temas açısı olarak adlandırılır ve minimum temas açısı geri çekilme açısı olarak adlandırılır. İlerleyen ve azalan temas açıları, damlacıkların veya sıvı köprülerin hareket halinde olduğu dinamik deneylerden ölçülür.[1] Aksine, Young-LaPlace denklemi tarafından tanımlanan denge temas açısı statik bir durumdan ölçülür. Statik ölçümler, biriktirme parametrelerine (örn. Hız, açı ve damla boyutu) ve düşme geçmişine (ör. Biriktirme zamanından buharlaşma) bağlı olarak ilerleyen ve azalan temas açısı arasında değerler verir. Temas açısı histerezisi şu şekilde tanımlanır: terim ifadeyi tanımlamak için de kullanılmasına rağmen . Statik, ilerleyen veya azalan temas açısı, uygulamaya bağlı olarak denge temas açısı yerine kullanılabilir.
İlerleyen temas açısı, sıvı-katı kaynaşmasının bir ölçüsü olarak tarif edilebilirken, geri çekilme temas açısı, sıvı-katı yapışmasının bir ölçüsüdür. İlerleyen ve azalan temas açıları doğrudan farklı yöntemler kullanılarak ölçülebilir ve ayrıca kuvvet tansiyometresi (diğer adıyla Wilhemy-Plate yöntemi) gibi diğer ıslatma ölçümlerinden de hesaplanabilir.
Damlalar bir yüzey üzerinde doğrusal olarak hareket ettirilirse, ilerleyen ve uzaklaşan temas açıları doğrudan aynı ölçümden ölçülebilir. Örneğin, bir sıvı damlası statik olduğunda belirli bir temas açısını benimser, ancak yüzey eğildiğinde damla ilk önce deforme olur, böylece damla ve yüzey arasındaki temas alanı sabit kalır. Damlalığın "yokuş aşağı" tarafı daha yüksek bir temas açısı benimseyirken, damlanın "yokuş aşağı" tarafı daha düşük bir temas açısı benimseyecektir. Eğim açısı arttıkça temas açıları değişmeye devam edecek, ancak damla ve yüzey arasındaki temas alanı sabit kalacaktır. Belirli bir yüzey eğim açısında ilerleyen ve azalan temas açıları karşılanacak ve damla yüzey üzerinde hareket edecektir. Uygulamada, eğer eğim hızı yüksekse ölçüm, kesme kuvvetleri ve momentumdan etkilenebilir. Ölçüm yöntemi ayrıca yüksek (> 30 derece) veya düşük (<10 derece) temas açısı histerezisi olan sistemler için pratikte zor olabilir.
İlerleme ve geri çekilme temas açısı ölçümleri, bir yüzeyde biriken bir damladan sıvı eklenerek ve çıkarılarak gerçekleştirilebilir. Bir damlaya yeterince az miktarda sıvı eklenirse, temas hattı sabitlenmeye devam eder ve temas açısı artar. Benzer şekilde, bir damladan az miktarda sıvı çıkarılırsa, temas açısı azalacaktır.
Young denklemi homojen bir yüzey alır ve yüzey dokusunu veya yerçekimi gibi dış kuvvetleri hesaba katmaz. Gerçek yüzeyler atomik olarak pürüzsüz veya kimyasal olarak homojen değildir, bu nedenle bir damla temas açısı histerezisi gerektirir. Denge temas açısı ( ) hesaplanabilir ve teorik olarak Tadmor[6] tarafından gösterildiği ve Chibowski[7] tarafından deneysel olarak doğrulandığı gibi,
nerede
Pürüzlü veya kontamine bir yüzeyde, temas açısı histerezisi de olacaktır, ancak şimdi yerel denge temas açısı (Young denklemi artık sadece yerel olarak geçerlidir) yüzeyde yer yer değişebilir.[8] Young-Dupré denklemine göre, bu, yapışma enerjisinin yerel olarak değiştiği anlamına gelir - bu nedenle, sıvının yüzeyi ıslatmak için yerel enerji bariyerlerinin üstesinden gelmesi gerekir. Bu bariyerlerin bir sonucu temas açısı histerezisidir : ıslanma derecesi ve dolayısıyla gözlenen temas açısı (temas hattı boyunca ortalama) sıvının yüzeyde ilerleyip ilerlememesine bağlıdır.
Sıvı daha önce kuru yüzey üzerinde ilerlediğinden, ancak daha önce ıslak yüzeyden uzaklaştığından, katının sıvı ile önceki teması (örneğin, kimyasal bir reaksiyon veya emilim yoluyla) nedeniyle değişmesi durumunda temas açısı histerezisi de ortaya çıkabilir. Bu tür değişiklikler, yavaşsa, ölçülebilir zamana bağlı temas açıları da üretebilir.
Pürüzlülüğün temas açılarına etkisi
Yüzey pürüzlülüğü, yüzeyin temas açısı ve ıslanabilirliği üzerinde güçlü bir etkiye sahiptir. Pürüzlülüğün etkisi, damlacıkların yüzey oluklarını ıslatmasına veya damlacık ile yüzey arasında hava ceplerinin bırakılmasına bağlıdır.[9]
Yüzey homojen olarak ıslaksa, damlacık Wenzel durumundadır.[10] Wenzel durumunda, yüzey pürüzlülüğü eklemek yüzeyin kimyasının neden olduğu ıslanabilirliği artıracaktır. Wenzel korelasyonu şu şekilde yazılabilir:
burada θ m ölçülen temas açısı, θ Y Genç temas açısı ve r pürüzlülük oranıdır. Pürüzlülük oranı, gerçek ve öngörülen katı yüzey alanı arasındaki oran olarak tanımlanır.
Yüzey heterojen olarak ıslatılırsa, damlacık Cassie-Baxter durumundadır.[11] En sabit temas açısı Genç temas açısına bağlanabilir. Wenzel ve Cassie-Baxter denklemlerinden hesaplanan temas açılarının, gerçek yüzeylere sahip en kararlı temas açılarının iyi bir tahmini olduğu bulunmuştur.[12]
Dinamik temas açıları
Sıvının bir yüzey üzerinde hızla hareket etmesi için, temas açısı hareketsizdeki değerinden değiştirilebilir. İlerleyen temas açısı hız ile artacak ve azalan temas açısı azalacaktır. Statik ve dinamik temas açıları arasındaki tutarsızlıklar, kılcal sayı ile yakından orantılıdır. .[1]
Temas açısı eğriliği
Arayüzey enerjileri temelinde, bir yüzey damlacıklarının profili veya iki yüzey arasındaki sıvı bir köprü Young-Laplace denklemi ile açıklanabilir.[1] Bu denklem üç boyutlu aksisimetrik koşullar için geçerlidir ve oldukça doğrusal değildir. Bu, damla şekli fonksiyonunun birinci ve ikinci dereceden türevlerinin ürünlerini içeren ortalama eğrilik teriminden kaynaklanmaktadır. :
Uygun sınır koşullarıyla birlikte üç boyutlu bir damlanın şeklini yöneten bu eliptik kısmi diferansiyel denklemin çözümü karmaşıktır ve buna alternatif bir enerji minimizasyonu yaklaşımı genel olarak benimsenir. Bu enerji minimizasyon yöntemi kullanılarak üç boyutlu sapsız ve asılı damlaların şekilleri başarılı bir şekilde tahmin edilmiştir.[13]
Tipik temas açıları
Temas açıları kirlenmeye karşı son derece hassastır; birkaç dereceden daha iyi tekrarlanabilir değerler genellikle sadece saflaştırılmış sıvılar ve çok temiz katı yüzeylere sahip laboratuvar koşullarında elde edilir. Sıvı moleküller katı moleküllere güçlü bir şekilde çekilirse, sıvı damlası 0 ° temas açısına karşılık gelen katı yüzey üzerinde tamamen yayılır. Bu genellikle çıplak metalik veya seramik yüzeylerde su için geçerlidir, ancak katı yüzeyde bir oksit tabakası veya kirletici madde bulunması temas açısını önemli ölçüde artırabilir. Genellikle, su temas açısı 90 ° 'den küçükse, katı yüzey hidrofilik olarak kabul edilir[14] ve su temas açısı 90 °' den büyükse katı yüzey hidrofobik kabul edilir. Birçok polimer hidrofobik yüzeyler sergiler. Düşük yüzey enerjili (örn. Florlu ) malzemelerden yapılmış yüksek hidrofobik yüzeyler, ang kadar yüksek su temas açılarına sahip olabilir. 120°'dir. Çok pürüzlü yüzeylere sahip bazı malzemeler, sıvı damlasının altında hava ceplerinin bulunması nedeniyle 150 ° 'den daha büyük bir su temas açısına sahip olabilir. Bunlara süperhidrofobik yüzeyler denir.
Temas açısı sıvı yerine gazla ölçülürse, verilen değerden 180 ° eksi ile değiştirilmelidir. Temas açıları, iki sıvının arayüzü için eşit olarak uygulanabilir, ancak yapışmaz tavalar ve su geçirmez kumaşlar gibi katı ürünlerde daha yaygın olarak ölçülürler.
Nilüfer (Lotus) Etkisi

Pek çok Asya kültüründe nilüfer çiçeği bitkisi saflığın ve temizliğin sembolü olarak bilinir. Bu düşüncenin temeli nilüfer bitkisi yapraklarının kendi kendini temizleme özelliğine dayanır. Bu kendi kendini temizleme özelliği tamamen araştırılmıştır ve yüzeyin yüksek derecede suyu itmesiyle sonuçlanan nilüfer yaprağının yüzeyi ile su arasındaki etkileşime bağlanmıştır. Yüksek derecede suyu itme karakteristiği ve kendi kendini temizlemenin nilüfer çiçeği bitkisi ile etkili biçimde gösterilmesine dayanarak Prof. Dr. W. Barthlott, bu etkileri Nilüfer (Lotus)Etkisi olarak tanımlamıştır.[15] Nilüfer etkisinin bulunuşu büyük teknolojik ilgi alanlarına yol açtı. Bu etkinin yapay yüzeylere taşınması ile birçok teknik uygulamalar elde edilmiştir. Nilüfer etkisi gösteren bir yüzey süperhidrofobiktir ve 150° den daha büyük temas açısını ifade eder. Süperhidrofobisitesine dayanarak, yüzey hafifçe meyillendirildiğinde su yüzeyde kayar ve yolu üzerindeki kirlilikleri yüzey üzerinden temizler. Lotus bitkisinin yapraklarının vaksla kaplanmış pürüzlü yüzeyi epidermal hücreler içermektedir. Vaks kristalleri su itici bir tabaka sağlamakta ve Wenzel ve Cassie Baxter modellerine göre yüzey pürüzlülüğünü artırmaktadır. Bu kristallerin ıslatma özelliği çok kötüdür. Bunun sonucu olarak, yüzey üzerindeki su damlası yüzeyle arasındaki etkileşimi en aza indirir. Böylece yüzeyde küresel bir damla oluşur. Yaprak yüzeyi üzerindeki kirlilikler yaprağın hücresel yapısından daha büyük olduğu için yüzey çıkıntıları üzerindeki partiküller yüzeyden uzaklaştırılabilir. Sonuç olarak temas alanı ve ara yüzeydeki etkileşim minimize edilmiş olur. Bir su damlası kirlilik üzerinde dönerek hareket ettiğinde, kirlilik hidrofobik özellikte olsa dahi absorpsiyon sayesinde enerji kazanılır. Eğer kirliliği lotus yaprağından uzaklaştırmak için harcanan enerji, su damlasının kirliliği absorbe etmesi ile kazandığı enerjiden daha az ise kirlilik bitki yüzeyinden uzaklaştırılmış olur. Bunun nedeni, genellikle küçük temas alanıdır.
Temas açılarının kontrolü
Islatma temas açısının kontrolü genellikle çeşitli organik ve inorganik moleküllerin yüzeye bırakılması veya dahil edilmesi yoluyla elde edilebilir. Bu genellikle bir SAM (kendi kendine monte edilen tekli katmanlar) katmanı oluşturabilen özel silan kimyasalları kullanılarak elde edilir. Değişen moleküler yapılara ve hidrokarbon ve / veya perfloronatlı sonlandırma miktarlarına sahip organik moleküllerin doğru seçilmesiyle, yüzeyin temas açısı ayarlanabilmektedir. Bu özel silanların biriktirilmesi, özel bir vakumlu fırınlar veya sıvı fazlı işlem kullanılarak gaz fazında elde edilebilir. Yüzeye daha perflorlanmış sonlandırmaları bağlayabilen moleküller, yüzey enerjisinin düşmesine (yüksek su temas açısı) neden olabilir.
| Yüzey florinin temas açısı üzerine etkisi | Su temas açısı |
|---|---|
| öncü | cilalı silikon (deg.) |
| Henikozil-1,1,2,2-tetrahydrododecyldimethyltris (dimethylaminosilane) | 118.0 |
| Heptadecafluoro-1,1,2,2-tetrahidrodesiltriklorosilan - (FDTS) | 110.0 |
| Nonaflor-1,1,2,2-tetrahydrohexyltris (dimetilamino) silan | 110.0 |
| 3,3,3,4,4,5,5,6,6-Nonafluorohexyltrichlorosilane | 108.0 |
| Tridecafluoro-1,1,2,2-tetrahidroositiltriklorosilan - (FOTS) | 108.0 |
| BİS (tridekaflor-1,1,2,2-tetrahydrooctyl) dimethylsiloxymethylchlorosilane | 107.0 |
| Dodesiltriklorosilan - (DDTS) | 105.0 |
| Dimetildiklorosilan - (DDMS) | 103.0 |
| 10-Undeseniltriklorosilan - (V11) | 100.0 |
| Pentafluorophenylpropyltrichlorosilane | 90.0 |
Ölçüm yöntemleri


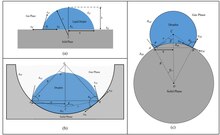
Statik sesil düşme yöntemi
Sapsız damla temas açısı, katı bir substrat üzerindeki saf bir sıvının profilini yakalamak için optik bir alt sistem kullanan bir temas açısı gonyometresi ile ölçülür. Sıvı-katı ara yüzü ile sıvı-buhar ara yüzü arasında oluşan açı temas açısıdır. Eski sistemlerde arka ışıklı mikroskop optik sistemi kullanılıyordu. Mevcut nesil sistemler, temas açısını yakalamak ve analiz etmek için yüksek çözünürlüklü kameralar ve yazılımlar kullanır. Bu şekilde ölçülen açılar genellikle ilerleyen temas açılarına oldukça yakındır. Denge temas açıları, iyi tanımlanmış titreşimlerin uygulanmasıyla elde edilebilir.[16]
Sarkıt damla yöntemi
Sarkıt damlalar için temas açılarının ölçülmesi, ters damlaların doğal dengesiz doğası nedeniyle sapsız damlalara göre çok daha karmaşıktır. Bu karmaşıklık, bir kişi yüzeyi eğmeye çalıştığında daha da artar. Eğimli yüzeyler üzerinde asılı damla temas açılarını ölçmek için deneysel cihaz son zamanlarda geliştirilmiştir.[17] Bu yöntem, yüksek çözünürlüklü bir CCD kamera kullanılarak görüntülenebilen, dokulu bir substratın altında birden fazla mikro damlanın birikmesine izin verir. Otomatik bir sistem, alt tabakanın eğilmesine ve ilerleyen ve azalan temas açılarının hesaplanması için görüntülerin analiz edilmesine izin verir.
Dinamik sesil bırakma yöntemi
Dinamik ses damlası düşmesi statik ses damlasına benzer, ancak damlanın değiştirilmesini gerektirir. Yaygın bir dinamik ses damlası çalışması, katı-sıvı arayüzey alanını dinamik olarak hacim ekleyerek arttırmadan mümkün olan en geniş temas açısını belirler. Bu maksimum açı ilerleyen açıdır. Hacim, mümkün olan en küçük açı olan geri çekme açısını üretmek için çıkarılır. İlerleyen ve azalan açı arasındaki fark temas açısı histerezidir .
Dinamik Wilhelmy yöntemi

Düzgün geometrili katılardaki ortalama ilerleme ve geri çekilme temas açılarını hesaplamak için bir yöntem. Katının her iki tarafı da aynı özelliklere sahip olmalıdır. Katı üzerindeki ıslatma kuvveti, katı bilinen yüzey gerilimi olan bir sıvının içine daldırılırken veya çekilirken ölçülür. Ayrıca bu durumda çok kontrollü bir titreşim uygulayarak denge temas açısını ölçmek mümkündür. VIECA adı verilen bu metodoloji, her Wilhelmy dengesinde oldukça basit bir şekilde uygulanabilir.[18]
Tek lif Wilhelmy yöntemi
İlerleyen ve azalan temas açılarını ölçmek için tek liflere uygulanan dinamik Wilhelmy yöntemi.

Tek lif menisküs yöntemi
Tek fiber Wilhelmy yönteminin optik bir varyasyonu. Bir terazi ile ölçüm yapmak yerine, lif üzerindeki menisküsün şekli, yüksek çözünürlüklü bir kamera kullanılarak doğrudan görüntülenir. Otomatik menisküs şekli uydurma, daha sonra, doğrudan lif üzerindeki statik, ilerleyen veya azalan temas açısını doğrudan ölçebilir.
Washburn denklemi kılcal yükselme yöntemi
Gözenekli bir malzeme olması durumunda, hem hesaplanan gözenek çapının fiziksel anlamı hem de bu denklemin, bu yöntem genellikle çok fazla yazılım tarafından sunulsa bile, katının temas açısının hesaplanması için gerçek olasılıkla ilgili birçok sorun ortaya çıkmıştır. konsolide olduğu gibi. Zamanın bir fonksiyonu olarak kilo ölçülür.[19]
Ayrıca bakınız
- Gonyometre
- Meniscus (liquid)
- Porosimetry
- Sessile drop technique
- Surface tension
- Wetting
Kaynakça
- ^ a b c d Shi (2018). "Dynamic contact angle hysteresis in liquid bridges". Colloids and Surfaces A: Physicochemical and Engineering Aspects. Cilt 555. ss. 365-371.
- ^ "III. An essay on the cohesion of fluids". Philosophical Transactions of the Royal Society of London. Cilt 95. Ocak 1805. ss. 65-87.
- ^ Josiah Willard Gibbs (1961). The Scientific Papers of J. Willard Gibbs (İngilizce). ISBN 978-0486607214.
- ^ a b c Jasper (Mayıs 2019). "A generalized variational approach for predicting contact angles of sessile nano-droplets on both flat and curved surfaces". Journal of Molecular Liquids. Cilt 281. ss. 196-203.
- ^ Jasper (Aralık 2017). "Relationship between contact angle and contact line radius for micro to atto [10−6 to 10−18] liter size oil droplets". Journal of Molecular Liquids. Cilt 248. ss. 920-926.
- ^ Tadmor (2004). "Line energy and the relation between advancing, receding, and Young contact angles". Langmuir. 20 (18). ss. 7659-64.
- ^ Chibowski (2008). "Surface free energy of sulfur—Revisited I. Yellow and orange samples solidified against glass surface". Journal of Colloid and Interface Science. 319 (2). ss. 505-13.
- ^ de Gennes (1985). "Wetting: statics and dynamics". Reviews of Modern Physics. 57 (3). ss. 827-863.
- ^ "Influence of surface roughness on contact angle and wettability" (PDF). 7 Kasım 2017 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 13 Nisan 2020.
- ^ Wenzel (1 Ağustos 1936). "Resistance of Solid Surfaces to Wetting by Water". Industrial & Engineering Chemistry. 28 (8). ss. 988-994.
- ^ Cassie (1 Ocak 1944). "Wettability of porous surfaces". Transactions of the Faraday Society. Cilt 40. s. 546.
- ^ Marmur (6 Temmuz 2009). "Solid-Surface Characterization by Wetting". Annual Review of Materials Research. 39 (1). ss. 473-489.
- ^ Chen Y, He B, Lee J, Patankar NA (2005). "Anisotropy in the wetting of rough surfaces" (PDF). Journal of Colloid and Interface Science. 281 (2). ss. 458-464. 10 Ağustos 2017 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 31 Mart 2017.
- ^ Renate Förch; Holger Schönherr; A. Tobias A. Jenkins (13 Temmuz 2009). Surface Design: Applications in Bioscience and Nanotechnology (İngilizce). John Wiley & Sons. ISBN 978-3-527-40789-7. 29 Temmuz 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 13 Nisan 2020.
- ^ "Sıvıların Islatma Yetenekleri ve Temas Açısı". 11 Kasım 2018 tarihinde kaynağından arşivlendi. Erişim tarihi: 14 Nisan 2020.
- ^ Volpe, C. D. (2006). "About the possibility of experimentally measuring an equilibrium contact angle and its theoretical and practical consequences". Contact Angle, Wettability and Adhesion. Cilt 4. ss. 79-100. 1 Ağustos 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 13 Nisan 2020.
- ^ Bhutani (2013). "Determination of apparent contact angle and shape of a static pendant drop on a physically textured inclined surface". Interfacial Phenomena and Heat Transfer. Cilt 1. ss. 29-49.
- ^ Volpe, C. D. (2001). "An experimental procedure to obtain the equilibrium contact angle from the Wilhelmy method" (PDF). Oil and Gas Science and Technology. Cilt 56. ss. 9-22. 15 Temmuz 2018 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 13 Nisan 2020.
- ^ Washburn, Edward W. (1921). "The Dynamics of Capillary Flow". Physical Review. 17 (3). s. 273. 30 Temmuz 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 13 Nisan 2020.
Konuyla ilgili yayınlar
- Pierre-Gilles de Gennes, Françoise Brochard-Wyart, David Quéré, Kılcallık ve Islatma Olayları: Damlalar, Kabarcıklar, İnciler, Dalgalar, Springer (2004)
- Jacob Israelachvili, Moleküller Arası ve Yüzey Kuvvetleri, Akademik Yayın (1985–2004)
- DW Van Krevelen, Polimerlerin Özellikleri, 2. gözden geçirilmiş baskı, Elsevier Bilimsel Yayınevi, Amsterdam-Oxford-New York (1976)
- Gianangelo Bracco; Bodil Holst (10 Ocak 2013). Surface Science Techniques (İngilizce). Springer. ISBN 978-3-642-34242-4. Gianangelo Bracco; Bodil Holst (10 Ocak 2013). Surface Science Techniques (İngilizce). Springer. ISBN 978-3-642-34242-4. Gianangelo Bracco; Bodil Holst (10 Ocak 2013). Surface Science Techniques (İngilizce). Springer. ISBN 978-3-642-34242-4.
- Clegg, Carl Temas Açısı Kolaylaştırdı28 Temmuz 2020 tarihinde Wayback Machine sitesinde arşivlendi., ramé-hart (2013), 978-1-300-66298-3
- Temas açısı Temas açısı deneyi []