Trigonometride tanjant teoremi üçgenin üç kenarının uzunluğu ve açıların tanjantları arasındaki ilişki hakkında bir teoremdir.
![{\displaystyle {\frac {a-b}{a+b}}={\frac {\tan[{\frac {1}{2}}(\alpha -\beta )]}{\tan[{\frac {1}{2}}(\alpha +\beta )]}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b7a4a3592aa66976f1d34bbbb403daa392f9fdf)
| Üçgen Türleri |  | |
|---|---|---|
| Yardımcı Elemanlar | ||
| Teoremler ve bağıntılar | ||
| Açı ölçü birimleri |  | |
|---|---|---|
| Trigonometrik fonksiyonlar & Ters trigonometrik fonksiyonlar | ||
| Referans | ||
| Yasalar ve teoremler | ||
| Kalkülüs | ||
| İlgili konular | ||
| Kullanıldığı dallar | ||
| Katkı sağlayan matematikçiler | ||
Trigonometri, üçgenlerin açıları ile kenarları arasındaki bağıntıları konu edinen matematik dalı. Trigonometri, sinüs ve kosinüs gibi trigonometrik işlevlerin (fonksiyon) üzerine kurulmuştur ve günümüzde fizik ve mühendislik alanlarında sıkça kullanılmaktadır.
Alman matematikçi David Hilbert'in 1871'deki bir makalesinde incelemiş olduğu hiperbolik geometri'nin Poincaré modeli için verdiği cebirsel geometrik yapı. Doğruların uçlarının oluşturduğu bir cisim ve bu cisim üzerinde tanımlı bir çarpımsal uzaklık fonksiyonu içeriyor. Öklit geometrisine ters olarak, doğruların koordinatları ve noktaların denklemleri bulunuyor.
Kotanjant, Trigonometrik bir fonksiyondur. 
Olasılık kuramı ve istatistikte, beta dağılımı, [0,1] aralığında iki tane pozitif şekil parametresi ile ifade edilmiş bir sürekli olasılık dağılımları ailesidir. Çok değişkenli genellemesi Dirichlet dağılımıdır.
Olasılık kuramı ve istatistik bilim dallarında gamma dağılımı iki parametreli bir sürekli olasılık dağılımıdır. Bu parametrelerden biri ölçek parametresi θ; diğeri ise şekil parametresi k olarak anılır. Eğer k tam sayı ise, gamma dağılımı k tane üstel dağılım gösteren rassal değişkenlerin toplamını temsil eder; rassal değişkenlerin her biri nin üstel dağılımı için parametre 
Olasılık kuramı ve istatistik bilim dallarında üstel dağılımı bir sürekli olasılık dağılımları grubudur. Sabit ortalama değişme haddinde ortaya çıkan bağımsız olaylar arasındaki zaman aralığını modelleştirirken bir üstel dağılım doğal olarak ortaya çıkar.
Üçgenlerle ilgili erken çalışmalar, Mısır matematiği ve Babil matematiğinde MÖ 2. binyıla kadar izlenebilir. Trigonometri, Kushite matematiğinde de yaygındı. Trigonometrik fonksiyonların sistematik çalışması Helenistik matematikte başladı ve Helenistik astronominin bir parçası olarak Hindistan'a ulaştı. Hint astronomisinde trigonometrik fonksiyonların incelenmesi, özellikle sinüs fonksiyonunu keşfeden Aryabhata nedeniyle Gupta döneminde gelişti. Orta Çağ boyunca, trigonometri çalışmaları İslam matematiğinde El-Hârizmî ve Ebu'l-Vefâ el-Bûzcânî gibi matematikçiler tarafından sürdürüldü. Altı trigonometrik fonksiyonun da bilindiği İslam dünyasında trigonometri bağımsız bir disiplin haline geldi. Arapça ve Yunanca metinlerin tercümeleri trigonometrinin Latin Batı'da Regiomontanus ile birlikte Rönesans'tan itibaren bir konu olarak benimsenmesine yol açtı. Modern trigonometrinin gelişimi, 17. yüzyıl matematiği ile başlayan ve Leonhard Euler (1748) ile modern biçimine ulaşan Batı Aydınlanma Çağı boyunca değişti.
Kosinüs teoremi, geometride, üçgen üzerinde iki kenarı ve aralarındaki açı verilmiş iken bilinmeyen kenarı bulmak amacıyla kullanılan formüldür. Şekil 1'deki üçgene göre kosinüs teoreminin uygulanışı şöyledir:
Klasik manyetizmanın eşdeğişimli formülasyonu klasik elektromanyetizma kanunlarının(özellikle de, Maxwell denklemlerini ve Lorentz kuvvetinin) Lorentz dönüşümlerine göre açıkça varyanslarının olmadığı, rektilineer eylemsiz koordinat sistemleri kullanılarak özel görelilik disiplini çerçevesinde yazılma sekillerini ima eder. Bu ifadeler hem klasik elektromanyetizma kanunlarının herhangi bir eylemsiz koordinat sisteminde aynı formu aldıklarını kanıtlamakta kolaylık sağlar hem de alanların ve kuvvetlerin bir referans sisteminden başka bir referans sistemine uyarlanması için bir yol sağlar. Bununla birlikte, bu Maxwell denklemlerinin uzay ve zamanda bükülmesi ya da rektilineer olmayan koordinat sistemleri kadar genel değildir.
Geometride, Thales teoremi, A, B ve C, AC çizgisinin bir çap olduğu bir daire üzerinde farklı noktalar ise, ∠ABC açısının bir dik açı olduğunu belirtir. Thales teoremi, çevre açı teoreminin özel bir durumudur ve Öklid'in Elemanlar adlı eserinin üçüncü kitabında 31. önermenin bir parçası olarak bahsedilmiş ve kanıtlanmıştır. Genellikle, teoremin keşif için şükran kurbanı olarak bir öküz sunduğu söylenen Miletli Thales'e atfedilir, ancak bazen Pisagor'a da atfedilir.
Özel fonksiyonların önemli bir bölümünü oluşturan hipergeometrik fonksiyonlar matematik, fizik, mühendislik ve olasılıkta karşımıza çıkar.
Stres-enerji tensörü, fizikte uzayzaman içerisinde enerji ve momentumun özkütle ve akısını açıklayan, Newton fiziğindeki stres tensörünü genelleyen bir tensördür. Bu, maddedinin, radyasyonun ve kütleçekimsel olmayan kuvvet alanının bir özelliğidir. Stres-enerji tensörü, genel göreliliğin Einstein alan denklemlerindeki yerçekimi alanının kaynağıdır, tıpkı kütle özkütlesinin Newton yerçekiminde bu tip bir alanın kaynağı olması gibi.
Öklid geometrisinde, Batlamyus teoremi, bir kirişler dörtgeninin dört kenarı ile iki köşegeni arasındaki bir ilişkiyi gösteridir. Teorem, Yunan astronom ve matematikçi Batlamyus'un adını almıştır. Batlamyus, teoremi astronomiye uyguladığı trigonometrik bir tablo olan kirişler tablosunu oluşturmaya yardımcı olarak kullandı.
Aristarchus eşitsizliği, eğer 
.Matematikte Hadwiger–Finsler eşitsizliği, Öklid düzlemindeki üçgen geometrisinin bir sonucudur. Düzlemdeki bir üçgenin kenar uzunlukları 
Bessel polinomları, matematikteki ortogonal polinomların bir dizisidir. Bessel polinomlarıyla ilgili birbirinden farklı ama birbiriyle yakından ilişkili çok sayıda tanım vardır. Matematikçiler tarafından tercih edilen tanım şu seriyle verilmektedir:
Trigonometride, trigonometrik özdeşlikler trigonometrik fonksiyonları içeren ve eşitliğin her iki tarafının da tanımlandığı değişkenlerin her değeri için doğru olan eşitliklerdir. Geometrik olarak, bunlar bir veya daha fazla açının belirli fonksiyonlarını içeren özdeşliklerdir. Bunlar üçgen özdeşliklerinden farklıdır, bunlar potansiyel olarak açıları içeren ama aynı zamanda kenar uzunluklarını veya bir üçgenin diğer uzunluklarını da içeren özdeşliklerdir.
Trigonometride, kotanjant teoremi veya kotanjantlar yasası, bir üçgenin kenar uzunlukları ile üç iç açısının yarılarının kotanjantları arasındaki ilişkidir.
Trigonometrik fonksiyonları tanımlamanın birkaç eşdeğer yolu vardır ve bunlar arasındaki trigonometrik özdeşliklerin kanıtları seçilen tanıma bağlıdır. En eski ve en temel tanımlar dik üçgenlerin geometrisine ve kenarları arasındaki orana dayanır. Bu makalede verilen kanıtlar bu tanımları kullanır ve dolayısıyla bir dik açıdan büyük olmayan negatif olmayan açılar için geçerlidir. Daha büyük ve negatif açılar için Trigonometrik fonksiyonlar bölümüne bakınız.
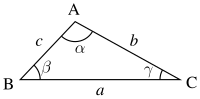
Trigonometride Mollweide formülü, bir üçgendeki kenarlar ve açılar arasındaki bir çift ilişkidir.