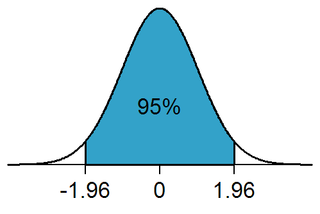
Student'in t testi

Student'ın t-testi istatistik bilimi içinde incelenen, eğer sıfır hipotez desteklenmekte ise test istatistiğinin bir Student's t-dağılımı gösterdiği hallerde uygulanan çıkartımsal istatistiksel hipotez sınamasıdır. Verilen iki değişik grup sayısal verinin birbirinden anlamlı olarak farklılık gösterip göstermemesini sınamak için kullanılabilir. En sıkça uygulanma örnekleri eğer test istatistiği içinde bulunan ölçek parametre faktörünün değerinin bir normal dağılım gösterdiği bilinmekte olduğu hallerde tatbik edilmektedir. Eğer test istatistiği içinde bulunan ölçek parametresi faktörünün değeri bilinmiyorsa ve bu faktör veriye dayayan bir kestirim ile ifade edilmekte ise (gayet iyice tanımlanmış özel belirli hallerde) test istatistiği bir Student'ın t-dağılımı gösterebilir.

t-test ve t-istatistiği kullanma ilk defa 1908'de Dublin, İrlanda'da önemli bir biracılık şirketi olan Guinness birasının kalitesini sınmak amacıyla bu bira fabrikasına özel olarak tutulmuş bir akademik kimyager olan (ve "Student" rumuzu ile akademik makalelerini imzalayan) William Sealy Gosset tarafından ortaya çıkartılmıştır ve kullanılmaya başlanmıştır. Guiness Şirketi'nin sahibi Claude Guinness imal ettiği bira ürününün tek bir yüksek standartta üretilmesini sağlamak Oxford Üniversitesi ve Cambridge Üniversitesi fen bilimleri mezunlarından en iyilerinden biyokimya ve istatistik bilimlerini pratikte sanayi imalat süreclerinde kullanmaya koyabilecek mezunlar istihdam etmeye önem vermekte idi. Gosset t-testini Dublin'de Guinness bira fabrikasının özel imalatı olan siyah ve yoğun "stout" adı verilen bira tipinin standart olarak üretilip üretilmediğini sınamak için ortaya çıkardı. Bu istatistiksel üretim kalitesi kontrol aracının geniş bir alanda da uygulanabileceği gayet açık olarak anlaşılmıştı. 1908'de Gosset ortaya çıkardığı "t-test" yöneteminin matematiksel olarak açıklanmasını bir bilimsel makale haline getirdi ve gayet itibarlı akademik bilimsel dergi olan "Biometrica" dergisine sundu. Bu dergi bu makaleyi yayınlamayı kabul etti. Fakat prensip olarak Guinness Şirketi bu sirkette çalışanlarin kendi isimleri ile makaleler yazıp bastırmalarına iyi bakmamakta idi. Bunun için Gosset Biometrika'da yayınlacak makalesi için kendi ismini kullanamadı ve makalesi "Student" rumuzu ile bastırıldı. Guinness ileri teknoloji kullanan çalışanlarına üniversiteler de ileri bilimsel çalışmalar yapmaları için akademik izin de vermekte idi. Gosset 1906-1907'de Londra Üniversitesi'ne bağlı olan University College'de Profesör Karl Pearson'un başı olduğu Biyometri Laboratuvarı'ndan çalışmaya başladı. O zaman Gossen'in ismi ve bilimsel ünü istatistikçiler ve biyometriciler tarafından bilinmekteydi ve bu akademik çalışmalar t-testinin geliştirilip kullanılıp yaygınlaştırılmasında önemli rol oynadılar. Fakat günümüze kadar çözümü bilinmeyen bir bilimsel sorun, istatistiksel t-testinin geliştirilmesinde Guinness firmasının pratik alanda yaptığı katkınin ne kadar olduğu ve Gosset'in Londra University College'de yaptığı akademik çalışmaların katkılarının ne olduğudur.

Değişik t-testlerinin en sık olarak kullanılanları arasında şunlar bulunmaktadır:

• Tek-örneklem konum testi:Tek anakütle ortalaması için parametrik hipotez sınaması veya μ için sınama. Anakütlenin ortalamasının sıfır hipotezi tarafından verilmiş olan değere eşit olup olmadığının sınanması.
• İki-örneklem konum testi: İki anakütle ortalaması farkı için hipotez sınaması veya iki anakitlenin Beklenen değerleri veya iki ana kütle ortalaması farkının (yani μ₁-μ₂) değerinin problemde verilen değere (çok kere 0 değere) eşit olup olmadığı için sınaması.

Pratik istatistiksel kullanımlarda "iki-örneklem konum testi" pratikte gayet genel olarak kullanılmaktadır. Fakat teorik bakımdan daha doğru ve sıkı düşünülürse "iki örneklem konum testi" ancak gayet belirli iki örneklem verileri için uygulanmması gerekmektedir. Bu belirli varsayımlara göre iki örneklemin kaynak olarak geldiği iki anakütlenin varyanslarının bilinmesi ve birbirine eşit olması gerekmektedir. Fakat pratik istatistik uygulamaların çoğunda bu eşit varyanslar varsayımı iki anakütle varyansının hiç ölçülmeden, sadece bir düşünce mahsulü olarak, eşit oldukları kabul edilmektedir. Bu tip düşünce mahsulü varyans eşitliği kabul edilmesinden sonra t-testinin uygulanmasını Welch'in t-testi olarak anıp bildirmek teorik olarak daha uygundur. Bu türlü elde edilen örneklem verilerine "eşlileştirme yapılmadan örneklem" veya "iki bağımsız örneklem" adı da verilmektedir. Bu "eşlileştirme yapılmadan örnekleme"'de iki değişik verilerin kaynağı olan iki "veri çerçevesi" bulunmaktadır ve bu iki veri çerçevesi içindeki veriler arasında bağımlılık bulunmamaktadır. "Eşlileştirme yapılmadan örnekleme" alınması halinde anakitle içinde bulunan her bir eleman, ancak tek bir örneklem içine girebilmekte ve eğer bir eleman bir çerçeve içine girmişse ikinci örneklem çerçevesi içinde bulunması imkânı olmaması gerekmektedir yani iki örneklem çerçevesinin birbiri üstüne binişmeleri ("överlepping" olmaları) imkânsızdır.^[1]

• Aynı anakütle elemanın yanı istatistiksel birimin üzerinde yapılan iki değişik ölçülme ile ortaya çıkan "eşlileştirilmiş örneklem" verileri ile yapılan ölçülme farklarının ortalaması için "t-testi". Bu testte sıfır hipotez anakitle için ölçüm farklarının ortalamasının 0 değere eşit olduğu sınanmaktadır. Örneğin, bir kanser hastasının tümörünün büyüklüğü ilk defa kanser ilacı vermeden önce ölçülmekte ikinci defa kanser ilacı verildikten sonra ölçüm alınmaktadır. Bu önce-ve-sonra seklindeki iki ölçüm arasındaki fark analiz için veridir yani kullanılan veri tek tek ölçüm değil birbirine bağımlı olarak tek elemanda (tek bir hastada) iki (tedaviden önce ve tedaviden sonra) ölçüm arasındaki farktır. Bu ölçümler sayica büyükçe bir örneklem hastalardan alınması gerekmektedir. Eğer tedavi efektif ise, birçok hasta için tümör büyüklüğünün ölçüm farklarının çoğunun negatif olması ve farklar ortalamasının sıfır altında olması beklenmektedir. Bu tip örneklem verileri için t-testine "eşlileştirilmiş örneklem t-testi" veya "tekrarlanmış ölçmeler için t-testi" adı verilmektedir.^[1][2]
• Doğrusal regresyon doğrusu'nun eğiliminin 0 değere eşit olup veya 0 değerden anlamlı olarak değişik olduğu.

İsim	Formül	Varsayımlar
İki-örneklem pool edilmiş t-testi	${\displaystyle t={\frac {({\overline {x}}_{1}-{\overline {x}}_{2})-(\mu _{1}-\mu _{2})}{s_{p}{\sqrt {{\frac {1}{n_{1}}}+{\frac {1}{n_{2}}}}}}},}$ ${\displaystyle s_{p}^{2}={\frac {(n_{1}-1)s_{1}^{2}+(n_{2}-1)s_{2}^{2}}{n_{1}+n_{2}-2}},}$ ${\displaystyle df=n_{1}+n_{2}-2\ }$	(Normal anakütle veya n1+n2 > 40) ve bağımsız gözlemler ve σ1 = σ2 ve (bilinmeyen σ1 ve σ2 değerleri)

İsim	Formül	Varsayımlar
İki-örneklem z-testi	${\displaystyle z={\frac {({\overline {x}}_{1}-{\overline {x}}_{2})-(\mu _{1}-\mu _{2})}{\sqrt {{\frac {\sigma _{1}^{2}}{n_{1}}}+{\frac {\sigma _{2}^{2}}{n_{2}}}}}}}$	Normal dağılım ve bağımsız gözlemler ve (bilinen σ1 ve σ1 değerleri)

İsim	Formül	Varsayımlar
İki-örneklem pool edilmemiş t-testi	${\displaystyle t={\frac {({\overline {x}}_{1}-{\overline {x}}_{2})-(\mu _{1}-\mu _{2})}{\sqrt {{\frac {s_{1}^{2}}{n_{1}}}+{\frac {s_{2}^{2}}{n_{2}}}}}},}$ ${\displaystyle df={\frac {(n_{1}-1)(n_{2}-1)}{(n_{2}-1)c^{2}+(n_{1}-1)(1-c)^{2}}},}$ ${\displaystyle c={\frac {\frac {s_{1}^{2}}{n_{1}}}{{\frac {s_{1}^{2}}{n_{1}}}+{\frac {s_{2}^{2}}{n_{2}}}}}}$ veya ${\displaystyle sd=\min\{n_{1},n_{2}\}-1\ }$	(Normal anakütleler veya n1+n2 > 40) ve bağımsız gözlemler ve σ1 ≠ σ2 ve (bilinmeyen σ1 ve σ2 değerleri)

İsim	Formül	Varsayımlar
Eşlileştirilmiş t-testi	${\displaystyle t={\frac {{\overline {d}}-d_{0}}{s_{d}}},}$ ${\displaystyle sd=n-1\ }$	(Normal farklar anakütlesi veya n < 30) ve bilinmeyen σ değeri

• Standart normal dağılım
• Student'in t dağılımı
• Anlamlılık seviyesi
• Hipotez testi
• Sıfır hipotez
• İ.Tur ve II.Tur hatalar
• p-değeri
• İki anakütle ortalaması farkı için hipotez sınaması
• Tek anakütle orantısı için parametrik hipotez sınaması
• İki anakütle orantısı farkı için parametrik hipotez sınaması

• Boneau, C. Alan (1960). "The effects of violations of assumptions underlying the t test". Psychological Bulletin c.57 no.:(1) say. 49–64. doi:10.1037/h0041412.
• Edgell, Stephen E., & Noon, Sheila M (1984). "Effect of violation of normality on the t test of the correlation coefficient". Psychological Bulletin c.95 no.(3) s. 576–583. doi:10.1037/0033-2909.95.3.576.

• O'Mahony, Michael (1986). Sensory Evaluation of Food: Statistical Methods and Procedures. CRC Press. s. 487. ISBN 0-82477337-3. (İngilizce)
• Press, William H.; Saul A. Teukolsky; William T. Vetterling; Brian P. Flannery (1992).Numerical Recipes in C: The Art of Scientific Computing. p. 616^[] Cambridge University Press. s 616. ISBN 0-521-43108-5. (İngilizce)

• Student'in t-testi hakkinda bir kavramsal makale28 Şubat 2015 tarihinde Wayback Machine sitesinde arşivlendi. (İngilizce)
• YouTube'da Econometri dersi konferansa (konu:hipotez sinamasi) sunucu: Mark Thoma (İngilizce)