Spiraller listesi

Bu Spiraller listesi, matematiksel olarak tanımlanan spiralleri içerir.

Resim	Ad	İlk Tanımlama	Denklem	Açıklama
	Çember		${\displaystyle r=k}$	tüm değişkenlerin sıfıra eşit olduğu (trivial) spiral
	Arşimet spirali	y. MÖ 320	${\displaystyle r=a+b\cdot \theta }$
	Euler spirali	1696	S(t) ve C(t) Fresnel integralleri olmak üzere kompleks düzlemde B(t)=S(t)+iC(t) noktalarının geometrik yeridir.	aynı zamanda Cornu spirali veya çokterimli (polinom) spiral olarak adlandırılır.
	Fermat spirali (aynı zamanda parabolik spiral)	1636[1]	${\displaystyle r^{2}=a^{2}\theta }$
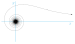
	Hiperbolik spiral	1704	${\displaystyle r=a/\theta }$	aynı zamanda ters spiral
	Lituus spirali	1722	${\displaystyle r^{2}\theta =k}$
	Logaritmik spiral	1638[2]	${\displaystyle r=a\cdot e^{b\theta }}$	yaklaşımları doğada da bulunur.
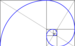
	Fibonacci spirali		dairesel yay, Fibonacci döşemesinde (sonsuz bir geometrik düzlemin birbirine uyumlu düzlem figürleriyle kaplanması) karelerin zıt köşelerini birbirine bağlar	altın sarmalın benzeri
	Altın spiral		${\displaystyle r=\varphi ^{\theta {\frac {2}{\pi }}}\,}$	logaritmik sarmalın özel durumu
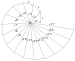	Theodorus sarmalı (veya Pisagor spirali)			Arşimet spiraline yaklaşan bitişik dik üçgenlerden oluşan poligonal bir spiral
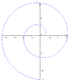	İçe kıvrık (involut)	1673
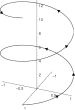	Helezon		${\displaystyle r(t)=1,\,}$ ${\displaystyle \theta (t)=t,\,}$ ${\displaystyle h(t)=t.\,}$	3-boyutlu bir spiral
	Kerte hattı (veya loksodrom)			bir küre üzerine çizilmiş spiral türü
	Cotes spirali	1722		Özel bir durumu epispirali başka bir özel durumu ise hiperbolik spirali verir.
	Poinsot spiralleri	1722?	${\displaystyle r=a\operatorname {csch} (n\theta ),\,}$ ${\displaystyle r=a\operatorname {sech} (n\theta )}$
	Nielsen spirali	1993[3]	${\displaystyle x(t)=\operatorname {ci} (t),\,}$ ${\displaystyle y(t)=\operatorname {si} (t)}$	Sinüs integralini ve kosinüs integrallerini kullanan Euler spiralinin bir varyasyonu
	Poligonal spiral			logaritmik sarmalın özel duruma ait benzeri
	Fraser Spirali	1908		Spirallere dayalı optik illüzyon
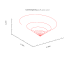	Conchospiral		${\displaystyle {\begin{cases}r=\mu ^{t}a\\\theta =t\\z=\mu ^{t}c\end{cases}}}$	bir koninin yüzeyindeki üç boyutlu spiral.
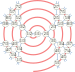	Calkin–Wilf spirali
	Ulam spirali (aynı zamanda asal sayı spirali)	1963
	Sack spirali	1994		Ulam spiralinin ve Arşimet spiralinin varyasyonu.
	Seiffert küresel spirali	2000	k pozitif bir sabit sayı ve sn(s) ile cn(s) Jacobi eliptik fonksiyonları olmak üzere ${\displaystyle {\begin{cases}r=sn(s,k),\\\theta =ks,\\z=cn(s,k)\end{cases}}}$	bir kürenin yüzeyindeki spiral eğri.
	Çekme eğrisi (Traktris) spirali	1704[4]	${\displaystyle {\begin{cases}r=A\cos(t)\\\theta =\tan(t)-t\end{cases}}}$
	Pappus spirali	1779	${\displaystyle {\begin{cases}r=a\theta \\\psi =k\end{cases}}}$	Pappus ve Pascal tarafından incelenen 3 boyutlu konik spiral[5]
	Doppler spirali		${\displaystyle {\begin{cases}x=a(t\cos(t)+kt)\\y=at\sin(t)\end{cases}}}$	Pappus spiralinin 2 boyutlu projeksiyonu[6]
	Atzema spirali		${\displaystyle {\begin{cases}x=\sin(t)/t-2\cos(t)-t\sin(t)\\y=-\cos(t)/t-2\sin(t)+t\cos(t)\end{cases}}}$	Katakostiği (yansıyan ışınların tek noktada toplanmasıyla oluşan eğri ya da yüzey) bir daire oluşturan olan eğri. Arşimet sarmalına yaklaşır.[7]
	Atomik spiral	2002	${\displaystyle r=\theta /(\theta -a)}$	Bu sarmalın iki asimptotu vardır; biri 1 birim yarıçaplı daire ve diğeri ${\displaystyle \theta =a}$ doğrusudur[8]

• Catherine çarkı (havai fişek)
• Sarmal galaksiler listesi
• Parker spirali
• Spirangle
• Spirograf