İçeriğe atla

Sistem tanılama

Sistem tanılama yöntemi

Sistem tanılama alanı, ölçülen verilerden dinamik sistemlerin matematiksel modellerini oluşturmak için istatistiksel yöntemleri kullanılır.[1] Durumu incelemek, donanım ve işletim sistemi ortamlarıyla ilgili sorunları bulmak için "sistem tanılama programları" kullanılır.[2]

Tarihçe

Parametrik sistem tanılama yöntemlerinin temeline inildiğinde karşımıza iyi bilinen istatistiksel yöntemlerden "en küçük kareler" ve "en büyük benzerlik" prensipleri çıkmaktadır. "En küçük kareler" yöntemi, doğrusal ve basit çoklu regresyon modellerinin çözümlenmesinde kullanılan temel aracı birim olarak çıkar. Bunun yanında çok denklemli ekonometrik çözümlemelerde de kullanılan tekniklerin ilkidir. "En büyük benzerlik" yöntemi de sistem tanılama hususuyla bağlantılı olarak veri gruplarına ait olasılık dağılımlarına temel teşkil eden parametrelerden çıkarımlarda bulunmaya yardım eden bir yöntemdir.

Bu yöntemlerin dinamik sistemlere uygulanabilir hale getirilmesi "modern kontrol teorisi"nin K.J. Aström ve I. Bohlin tarafından yayımlanan makaleleriyle (“Numerical Identification of Linear Dynamic Systems From Normal Operating Records”, 1965) 1960'lara rastlar. Sistem tanılama için geliştirilen bu tekniklerin endüstriyel süreçler için uygulanması ise Lennart Ljung ile başlamıştır (“The System Identification Toolbox”, 1986). Günümüzde her ne kadar yeni bir alan olarak görülebilir olsa da sistem tanılama ve dallarına ait edebiyat çok geniştir. Eykhoff (1974); Goodwin & Payne (1977) ; Söderström & Stocia (1989); Lennart Ljung'un (1987) eserleri bu konuya temel teşkil eden kaynaklardır.

Uluslararası Otomatik Kontrol Federasyonu (IFAC: International Federation of Automatic Control), sistem tanılama adına birçok makale sunulmasına; üretilmiş veya keşfedilmiş bilgilerin yaygınlaşmasına imkân veren "Tanılama ve Sistemlerin Parametre Yöntemleri Sempozyumu"'nu (Symposia on Identification and System Parameter Estimation) düzenlemektedir. Bu sempozyumlar, ilki 1967 yılında Prag'da gerçekleştirildiğinden beri, her üç senede bir yapılmaya devam etmektedir.

Gerçek yaşama dair nesnelerin matematiksel modellerini yapmanın felsefi sorgulamaları ilk defa 1934 yılında Karl Popper tarafından tartışılmaya açılmıştır. Fiziksel yasaların mühendislik uygulamalarındaki modellenmesi ise Wellstead (1979), Ljung & Glad (1994), Cellier (1990) ve buna benzer birçok bilim insanınca tartışılmaya sunulmuştur. Sistem tanılama konusunun yazımlarının ve kitaplarının temelini oluşturmuş ve geliştirmiş bu çabalar, aynı zamanda günümüzde de ilerlemesini sürdüren sistem tanılamanın destek birimlerini oluşturmaktadır. Bu bilimsel eserler, sistem tanılamanın başka unsurlarla harmanlanmasına olanak sağlamıştır. Bunlardan birkaçına burada atıfta bulunmak gerekli gözükmektedir:

Granger & Newbold, Malinvaud ekonomi alanında; Godfrey ve Mendel biyolojide; Robinson & Treitel jeolojide; Dudley elektromanyetik dalgalar konusunda; Markel & Gray ses dalgaları alanında modelleme ve tanılama araçlarını farklı uygulama alanlarında kullanan bilim insanlarından ilk çalışma sahipleridir.

Sistem tanılama tekniği

Sistem tanılama, dinamik bir sistemin modelinin gerçek sistemden alınan giriş-çıkış ölçümleriyle bulunması anlamına gelir. Sistem tanılamanın amacı, belirli bir sisteme veri giriş-çıkışı ilişkisinden, daha sonra sistem üzerinde tekrar yapılacak çalışmalarda kullanılabilecek güvenilir bir matematiksel model kurmaktır. Bu model;

  • Sistem davranışlarının öngörülebilmesini
  • Sistem davranışının istenilen yönde kontrol edilmesi ve yönlendirilebilmesini hedef edinir.

Bu çalışmanın ön koşulu gerçeği yansıtmaktır. Sistem tanılama yöntemleriyle elde edilen bir model, bir giriş ve bir çıkış arasındaki matematiksel ilişkiyi ortaya koymak amacıyla oluşturulabileceği gibi, birçok çıkış (veya ölçüm) ile birçok giriş arasındaki ilişkiyi de inceleyebilir.

Sistem tek giriş-tek çıkışlı ise SISO (single input-single output), çok giriş bir çıkışlı ise MISO (multi input- single output), çok girişli-çok çıkışlı ise MIMO (multi input-multi output) sistem olarak adlandırılır.

Sistem tanılama süreci, deneysel planlama ve veri toplama, modellerin kurulması, deney verilerinden bilinmeyen sistem parametrelerinin tahmin edilmesini ve bulunan modelin geçerliliğinin test edilmesini içerir. Yukarıda bahsedildiği gibi sistem modelinin bilinmesi, sistem karakteristiklerinin formülize edilmesi ve buna dayanarak yüksek performanslı kontrol sistemlerinin tasarımı ve oluşturulması için önemlidir.

Sistem tanılama izleği 4 ana aşamadan oluşur:

  1. Deneysel planlama
  2. Model yapısının seçimi
  3. Parametre kestirimi
  4. Kurulan modelin geçerliliğinin test edilmesi.

Sistemin geçerli bir matematik modelinin elde edilmesi başından sonuna kadar dikkat ve titizlik gerektiren bir işlemdir.

Sistem tanılama işlemi, sistemi uyaracak uygun giriş sinyalinin seçimi ile başlar. Sistemden elde edilen tanılamaya uygun veri ile bir model belirlenir ve belirlenen bir yöntemle parametreler kestirilir. Bu yolla elde edilen model geçerlilik testlerini geçemezse algoritmada yukarıdan aşağıya doğru hareket edilir. Önce parametre kestirim yöntemi değiştirilir. Eğer model çeşitli denemelere rağmen yine geçersizse model yapısı değiştirilir ve algoritmada aşağıya doğru hareket edilir. Model yapısını da değiştirmenin bir sonuca varmadığı durumlarda sistemin deneysel planlamasına geri dönülür. Sistemin lineer bir modelle temsil edilemediği veya tanılamanın (hata ölçülerine göre) yeteri kadar başarılı bulunmadığı sonucuna varılırsa akıllı sistemlerin de içinde bulunduğu lineer olmayan modelleme yapılarına başvurulur.

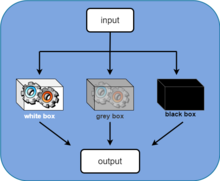
Sistem tanılamada iki yaklaşım

  • Gri Kutu: İncelenen sistemin yapısı hakkında bir önbilginin mevcut olması neticesinde kullanılan yaklaşımdır. Buna şu şekilde örnek verilebilir: Bir teknik resim hocası, teknik resim dersinde bir öğrencisinden “tolerans nedir?” sorusu alır. Teknik resim hocası da bir cevap verir. Teknik resim hocası cevabını verirken, soruyu soran öğrencinin kendi üniversitesinden olduğunu, konu hakkında bir bilgi birikimi sahibi olduğunu; neleri anlayabilir durumda olduğunu bilmektedir. İşte bu örnek de, sistem tanılamadaki “grey-box” yaklaşımının hayali bir özetidir. Bu yaklaşımda içeriği hakkında bir önbilgiye sahip olduğumuz bir sisteme bilinçli girişler yapılarak ve bunun sonucunda çıkan çıkışları izleyerek bir model oluşturulur.
  • Kara Kutu: İncelenen sistemin yapısı hakkında hiçbir bilgiye sahip olunmadığında kullanılan yaklaşımdır. Buna şu şekilde örnek verilebilir: Bir teknik resim hocası, yolda yürürken yanından geçen bir adam onu durdurur ve “tolerans nedir?” diye sorar. Teknik resim hocası, karşısındaki kimse hakkında bir bilgiye sahip değildir. Soruya vereceği cevaptan evvel öğrenmesi gerekenler mevcuttur. İşte bu örnek, sistem tanılamadaki “black-box” yaklaşımının hayali bir özetidir. Bu yaklaşımda, içeriğinden haberdar olmadığımız bir sisteme çeşitli girişler yapılarak ve bunun sonunda çıkan çıkışları da izleyerek bir model oluşturulur.

Kaynakça

  1. ^ Torsten; Stoica, P. (1989). System identification. New York: Prentice Hall. ISBN 978-0138812362. OCLC 16983523. 
  2. ^ "Sistem tanılama programlarının çalıştırılması". IBM Documentation. 31 Mart 2023. 20 Şubat 2024 tarihinde kaynağından arşivlendi. Erişim tarihi: 20 Şubat 2024. 
  1. Söderstöm, Torsten ve Stocia, Petre: System Identification, Prentice Hall International Series in Systems and Control Engineering
  2. Melsa, Sage: System Identification, Mathematics in Science and Engineering, Vol 80
  3. Ljung, Lennart: System Identification: Theory for the User, PTR Prentice Hall Information and System Sciences Series [1] 4 Şubat 2007 tarihinde Wayback Machine sitesinde arşivlendi.
  4. Kızılaslan, Kemal: Çimento Endüstrisinde Hammadde Harmanlama Prosesinin Klasik ve Akıllı Yöntemler Kullanarak Modellenmesi, İstanbul Teknik Üniversitesi Fen Bilimleri Enstitüsü, 2003
  5. A MANUAL FOR SYSTEM IDENTIFICATION

İlgili Araştırma Makaleleri

<span class="mw-page-title-main">Matematik</span> nicelik, yapı, uzay ve değişim gibi konularla ilgilenen bilim dalı

Matematik ; sayılar, felsefe, uzay ve fizik gibi konularla ilgilenir. Matematikçiler ve filozoflar arasında matematiğin kesin kapsamı ve tanımı konusunda görüş ayrılığı vardır.

Psikoterapi, bireylerin duygusal ve davranışsal sorunlarının çözümünü, ruh sağlıklarının geliştirilmesi ve korunmasını amaçlayan tekniklerin genel adı. Psikoterapi her zaman sadece tek tek bireyleri konu almaz, zaman zaman incelenen tüm bir ailenin etkileşimsel meseleleri zaman zamansa incelenen bir çiftin birbiriyle olan ilişkisindeki bazı sorunların ruh sağlığı temelindeki kökleri olabilir. Ruh-zihin sağlığına dair sorunların psikolojik, sosyolojik veya somatik boyutları olabilir.

<span class="mw-page-title-main">İstatistik</span>

İstatistik veya sayım bilimi, belirli bir amaç için veri toplama, tablo ve grafiklerle özetleme, sonuçları yorumlama, sonuçların güven derecelerini açıklama, örneklerden elde edilen sonuçları kitle için genelleme, özellikler arasındaki ilişkiyi araştırma, çeşitli konularda geleceğe ilişkin tahmin yapma, deney düzenleme ve gözlem ilkelerini kapsayan bir bilimdir. Belirli bir amaç için verilerin toplanması, sınıflandırılması, çözümlenmesi ve sonuçlarının yorumlanması esasına dayanır. Bu çerçevede yapılan işlemlerin tümüne sayımlama denir.

<span class="mw-page-title-main">Simülasyon</span> gerçek bir dünya süreci veya sisteminin işletilmesinin zaman üzerinden taklit edilmesi

Simülasyon veya benzetim, teknik olmayan anlamda bir şeyin benzeri veya sahtesi anlamında kullanılır. Teknik anlamda gerçek bir dünya süreci veya sisteminin işletilmesinin zaman üzerinden taklit edilmesidir. Sistem nesneleri arasında tanımlanmış ilişkileri içeren sistem veya süreçlerin bir modelidir.

Gerçel analiz ya da bilinen diğer ismiyle reel analiz, matematiksel analizin bir dalıdır. Bu dal, gerçek sayılar ve bu sayılardan türetilen yapılarla ilgili temel kavramları ele alır. Ana konuları arasında diziler, seriler, limitler, süreklilik, türev, integral ve fonksiyon dizileri yer alır. Gerçek analizin incelenmesi, matematiğin diğer alanları için temel araçlar ve yöntemler sağlar.

<span class="mw-page-title-main">Hesaplamalı fizik</span>

Hesaplamalı fizik, fizik sorunlarını çözebilmek için sayısal algoritmaların üretilmesi ve gerçeklenmesini içerir. Genelde kuramsal fizikin bir alt dalı olarak değerlendirilir ancak bazen de kuramsal ve deneysel fizik arasında orta bir dal olarak da düşünülür.

Matematiksel model, bir sistemin matematiksel kavramlar ve dil kullanılarak tanımlanmasıdır. Matematiksel model geliştirme süreci, matematiksel modelleme olarak adlandırılır. Matematiksel modeller, doğa bilimlerinde ve mühendislik disiplinlerinde bunun yanı sıra sosyal bilimlerde kullanılır. Matematiksel modelleri daha çok fizikçiler, mühendisler, istatistikçiler, operasyon araştırma analistleri ve ekonomistler kullanır. Model, bir sistemi açıklamaya, farklı bileşenlerin etkilerini incelemeye ve bir davranış hakkında öngörüde bulunmak için yardımcı olabilir.

Ağ'a bağlı aygıtların birbirleri ile haberleşmesi için kullanılan bir API 'dir. NetBIOS, Network Basic Input/Output System 'in kısaltmasıdır. Bu, ayrı bilgisayarlarda yerel alan ağı üzerinden iletişim kurmak için OSI Modelini sağlayan uygulamaların oturum katmanı ile ilgili hizmet vermektedir. NetBIOS bir ağ protokolü değildir sadece bu protokol üzerinde çalışan bir API'dir.

<span class="mw-page-title-main">Süperpozisyon prensibi (fizik)</span> Bir parçacık veya sistemin belli bir zamanda birden fazla durumda olabilmesi.

Fizikte ve sistem teorisinde, süperpozisyon prensibi, tüm lineer sistemler için bir veya daha fazla uyarılar tarafından oluşan net tepki olarak belirtilen süper pozisyon özelliği olarak da bilinir. Kuantum mekaniğinde iki dolanık parçanın durumuna da süperpoziyon denilir. Bu uyarılar her bir uyarıcı tarafından tek tek meydana gelen uyarıların toplamıdır. Eğer giriş A, X tepkisini üretirse ve giriş B, Y tepkisini üretirse, sonuç olarak giriş (A+B), (X+Y) tepkisini üretir. Homojenlik ve eklenebilirlik özellikleri birlikte süperpozisyon prensibi olarak adlandırılır. Bir lineer fonksiyon süperpozisyon prensibini sağlayanlardan biridir ve şöyle tanımlanır:

 Eklenebilirlik
  Homojenlik
skaler a için.

Uyarlamalı ağ tabanlı bulanık çıkarım sistemi, Takagi-Sugeno bulanık çıkarım sistemine dayalı bir tür yapay sinir ağı yöntemi. Jang tarafından 1990’ların başlarında geliştirilmiş olup doğrusal olmayan fonksiyonların modellenmesinde ve kaotik zaman serilerinin tahmininde kullanılmıştır.

<span class="mw-page-title-main">İşlev modeli</span>

Sistem ve yazılım mühendisliğindeki işlev modeli modellenen sistem veya konu alanının işlevlerinin yapısal temsilidir.

Kavramsal model bir sistemin temsilidir ve modelin temsil ettiği sistemin insanların daha rahat bir şekilde anlamalarına yardımcı olur. Örneğin, montajı yapılarak oluşturulan bir oyuncak model temsil ettiği objenin çalışmasını modelini oluşturacak bir şekilde çalışabilir.

Hesaplamalı kimya, kimya problemlerini çözmeye yardımcı olmak için bilgisayar simülasyonunu kullanan bir kimya dalıdır. Moleküllerin, katıların yapı ve özelliklerini hesaplamak için verimli bilgisayar programlarına dahil edilmiş teorik kimya yöntemlerini kullanır. Bu yöntemlerin kullanılmasının nedeni, hidrojen moleküler iyonu ile ilgili nispeten yeni sonuçlar dışında, kuantum çok-gövdeli(many-body) problemlerin analitik olarak çözülemez oluşudur. Hesaplama sonuçları normal olarak kimyasal deneylerle elde edilen bilgileri tamamlarken, bazı durumlarda gözlemlenmeyen kimyasal olayları da tahmin edebilmektedir. Yeni ilaç ve materyallerin tasarımında yaygın olarak kullanılmaktadır.

<span class="mw-page-title-main">Bilimsel hesaplama</span>

Bilimsel hesaplama karmaşık problemleri anlamak ve çözmek için gelişmiş bilgi işlem yeteneklerini kullanan çok disiplinli bir alandır. Hesaplamalı bilim üç farklı unsuru birleştirmektedir:

<span class="mw-page-title-main">Matematiksel istatistik</span> matematiksel yöntemlerin kullanıldığı olası istatistikler

Matematiksel istatistik, istatistiksel veri toplama tekniklerinin aksine, matematiğin bir dalı olan olasılık teorisinin istatistiğe uygulanmasıdır. Bunun için kullanılan özel matematiksel teknikler arasında matematiksel analiz, doğrusal cebir, stokastik analiz, diferansiyel denklemler ve ölçü teorisi bulunur.

Perceptron (Algılayıcı), tek katmanlı bir yapay sinir ağının temel birimidir. Eğitilebilecek tek bir yapay sinir hücresinden oluşmaktadır. Denetimli bir öğrenme algoritmasıdır. Bir perceptron giriş değerleri, ağırlıklar ve sapma, ağırlıklı toplam ve aktivasyon işlevi olmak üzere dört bölümden oluşmaktadır. Hem giriş hem de çıkış değerleri verilir ve sinir ağının öğrenmesi beklenir.

<span class="mw-page-title-main">Bilgisayarlı görü</span> görsellerden veri bilgisi çıkartmak

Bilgisayarlı görü, bilgisayarların dijital görüntülerden veya videolardan nasıl bir anlam kazanabileceğiyle ilgilenen disiplinler arası bilimsel bir alandır. Mühendislik yöntemleriyle, insan görsel sisteminin yapabileceği görevleri anlamaya ve otomatikleştirmeye çalışmaktadır.

Adaptif rezonans teorisi (ART), Stephen Grossberg ve Gail Carpenter tarafından beynin bilgiyi nasıl işlediğini anlamak üzere geliştirilen bir teoridir. Denetimli ve denetimsiz öğrenme yöntemlerini kullanan ve örüntü tanıma ve tahmin gibi sorunları ele alan bir dizi sinir ağı modelini açıklamaktadır.

SHARE İşletim Sistemi SHARE kullanıcı grubu tarafından 1959 yılında tanıtılımış bir işletim sistemidir. General Motors'un GM-NAA I/O adlı işletim sisteminin geliştirilmiş bir sürümüdür ve IBM 704 için geliştirlmiş ilk işletim sistemidir. Ana amaç programların paylaşımını geliştirmekti.

Doğrudan ses girişi (DSG),, bazen ses girişi denetimi olarak da adlandırılır, kullanıcının makineye konuşma tanıma yoluyla talimatlar vermek için sesli komutlar ilettiği bir insan-makine etkileşimi biçimidir.


Bu sayfa, bu Vikipedi makalesine dayanmaktadır.
Metin, CC BY-SA 4.0 lisansı altında mevcuttur; ek koşullar uygulanabilir.
Görseller, videolar ve sesler kendi lisansları altında mevcuttur.