
Jeodezi ya da yerölçüm, yerkürenin modellenmesiyle, yerkürede ve dış alanında dört boyutlu kesin koordinat sistemlerini tanımlayan, referans ağlarını oluşturan, mekansal bilgileri bu ağ ve sistemlerle ilişkilendiren ve zamana bağlı değişimini izleyen ve genel anlamda yerkürenin şeklini tespit ve yeryüzünü ölçme işlemlerini konu edinen bilim dalı.

Tutulum, ekliptik veya tutulum düzlemi ya da ekliptik düzlem, Dünya'nın Güneş etrafındaki yörünge düzlemidir. Dünya'da bulunan bir gözlemcinin bakış açısından, Güneş'in bir yıl boyunca gök küre etrafındaki hareketi, yıldızların arka planına karşı ekliptik boyunca bir yol izler. Ekliptik önemli bir referans düzlemidir ve ekliptik koordinat sisteminin temelidir.
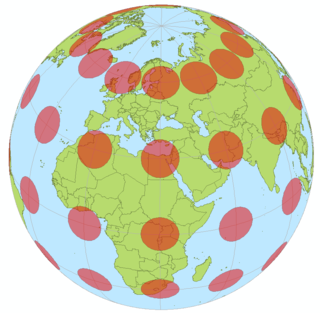
Harita projeksiyonu, 3 boyutlu yeryüzünün matematiksel transformasyon ile iki boyutlu düzlemde temsil edilmesi işlemine denir. Harita projeksiyonunun yeryüzünün şeklini nasıl değiştirdiğini anlamanın kolay bir yolu merkezinde bir ışık kaynağı bulunduğu varsayılan yeryüzünün projeksiyon yüzeyi denen bir yüzeye iz düşürülmesidir.

Takımyıldız, gökyüzünün bölündüğü 88 alandan her birine verilen isimdir. Terim genellikle, yanlış bir biçimde, görünüşte birbiriyle ilgili gözüken yıldız gruplarını tanımlamak için kullanılır.

Atalet momenti veya eylemsizlik momenti, dönmekte olan bir cismin, dönme hareketine karşı durmasına eylemsizlik momenti denir. Eylemsizlik momenti, toplam dönme hareket gücüne karşı direnç oluşturur ve bu yüzden cisim, tam verimde dönemez.
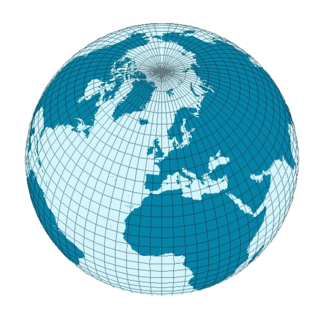
Coğrafi koordinat sistemi, dünya üstündeki herhangi bir yeri, topografik bir nokta olarak tanımlamayı sağlayan bir koordinat sistemi. Küresel koordinat sistemindeki üç bileşenden ikisi kullanılarak belirtilir. Burada aşılması gereken zorluk, dünyanın bir küre değil de jeodezi bağlamında yaklaşık olarak bir elipsoit ya da basık sferoit şeklinde olmasıdır.

Küresel koordinat sistemi, üç boyutlu uzayda nokta belirtmenin bir yoludur.
Koordinat sistemi, geometride herhangi bir düzlemdeki (çokkatlıdaki) bir nokta veya başka bir geometrik elemanın konumunu tam olarak belirlemek için bir veya daha çok sayı ya da koordinat kullanılan bir sistemdir. Koordinatlar basit matematikteki reel sayılardan oluşur. Fakat soyut cebir gibi bazı alanlarda karmaşık sayılar veya elemanlardan oluşabilir. Koordinat sisteminin kullanılması, geometrik problemlerin sayısal problemlere ve tersine dönüştürülmesini sağlar. Bu analitik geometrinin temelidir.
Kutup aşağıdaki anlamlara gelebilir:

 Kartezyen çarpımındaki
Kartezyen çarpımındaki
- her sıralı ikilinin Öklid düzlemindeki bir noktaya ve
- birinci dereceden iki değişkenli her bir polinomun düzlemdeki bir doğruya, birebir eşlenmesi ile oluşturulan cebirsel geometrik yapıya Kartezyen koordinat sistemi veya Dik eksenler sistemi adı verilir. Öklid geometrisinin bir modelidir. Koordinat eksenleri x ve y eksenidir bunlar 0 da çakışır. Çakışılan yere sıfır noktası (orijin) adı verilir.

Matematikte kutupsal koordinat sistemi veya polar koordinat sistemi, noktaların birer açı ve Kartezyen koordinat sistemindeki orijinin eşdeğeri olup "kutup" olarak bilinen bir merkez noktaya olan uzaklıklar ile tanımlandığı, iki boyutlu bir koordinat sistemidir. Kutupsal koordinat sistemi, matematik, fizik, mühendislik, denizcilik, robot teknolojisi gibi birçok alanda kullanılır. Bu sistem, iki nokta arasındaki ilişkinin açı ve uzaklık ile daha kolay ifade edilebildiği durumlar için özellikle kullanışlıdır. Kartezyen koordinat sisteminde, böyle bir ilişki ancak trigonometrik formüller ile bulunabilir. Kutupsal denklemler, çoğu eğri tipi için en kolay, bazıları içinse yegâne tanımlama yöntemidir.

Yarıçap, bir daire veya kürenin özeğinin (merkezinin) çemberine olan mesafesidir. Çapın yarısına eşittir.

Matematikte karmaşık düzlem, gerçel eksen ve ona dik olan sanal eksen tarafından oluşturulmuş, karmaşık sayıların geometrik bir gösterimidir. Karmaşık sayının gerçel kısmının x-ekseni boyuncaki yer değiştirmeyle, sanal kısmının ise y-eksenindeki yer değiştirmeyle temsil edildiği değiştirilmiş bir Kartezyen düzlem olarak düşünülebilir.

Gökküre, Gökbilim ve seyrüseferde, Dünya'yla eşmerkezli ve eşeksenli, devasa çaplı varsayımsal bir küredir. Gökyüzündeki tüm cisimlerin iç yüzeyinde yer aldığı bir küre şeklinde düşünülebilir. Gök ekvatoru yer ekvatoruyla, gök kutupları da yerin kutup noktalarıyla aynı doğrultuda çakışıktır. Gökküre yansıtması gökcisimlerinin konumlarının belirlenmesi için çok pratik bir yöntemdir.
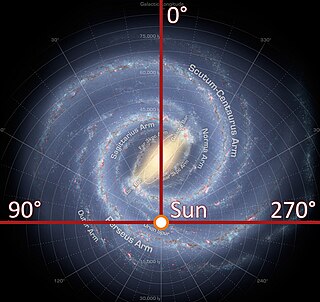
Galaktik koordinat sistemi, Güneş'i merkez alarak, ana yönü Samanyolu Gökadası'nın yaklaşık merkeziyle hizalı ve temel düzlemi galaktik düzleme paralel olan bir gökyüzü koordinat sistemidir. Sağ el kuralını kullanır, yani koordinatlar temel düzlemde kuzeye ve doğuya doğru pozitiftir.
Astigmatizm (veya Astigmatizma) ile bir optik sistemde, iki dik düzlemde yayılan ışınların farklı odaklara sahip olduğu bir sistem sorunudur. Bir çarpı görüntüsünü oluşturmak için astigmatizma ile optik bir sistem kullanılırsa, dikey ve yatay çizgiler iki farklı mesafede keskin odakta olacaktır. Terim, "yok" anlamına gelen Yunanca α- (a- ) ve στίγμα ( stigma), ("bir işaret, nokta, delinme" anlamına gelen") birleşiminden oluşmuştur.

Çıkış düğümü boylamı, bir nesnenin uzaydaki yörüngesini belirtmek için kullanılan yörünge ögelerinden biridir. Belirtilen bir referans düzleminde ölçüldüğü gibi, boylamın orijini olarak adlandırılan belirli bir referans yönünden çıkış düğümün yönüne olan açıdır. Çıkış düğümü, bitişik görüntüde görüldüğü gibi, nesnenin yörüngesinin referans düzleminden geçtiği noktadır. Yaygın olarak kullanılan referans düzlemleri ve boylamın kökenleri şunları içerir:
- Yer merkezli yörüngeler için, referans düzlemi olarak Dünya'nın ekvator düzlemi ve boylamın başlangıcı olarak Koç'un ilk noktası. Bu durumda boylam, çıkış düğümün sağ açıklığı (RAAN) olarak da adlandırılır. Açı, Koç'un ilk noktasından düğüme doğuya doğru ölçülür. Bir alternatif, uzay aracının ekvatoru geçtiği yerel ortalama zamana dayanan, çıkış düğümün yerel saatidir (LTAN). Diğer gezegenlerin etrafındaki uydular için de benzer tanımlar mevcuttur.
- Güneş merkezli yörüngeler için, referans düzlemi olarak ekliptik ve boylamın başlangıcı olarak Koç'un ilk noktası. Açı, Koç'un ilk noktasından düğüme kadar saat yönünün tersine ölçülür.
- Güneş Sistemi dışındaki yörüngeler için, referans düzlemi olarak ilgi noktasında gökküresine teğet olan düzlem ve kuzey gökyüzü düzlemine) boylamın kökeni olarak. Açı, kuzeyden düğüme doğuya doğru ölçülür., pp. 40, 72, 137; , chap. 17.
Referans düzlemi, gök mekaniğinde yörünge öğelerini tanımlarken kullanılan bir düzlemdir. Referans düzlemine göre tanımlanan iki ana yörünge öğesi yörünge eğikliği ve çıkış düğümü boylamıdır.

Yörünge düzlemi, dönen bir cismin yörüngesinin içinde bulunduğu geometrik bir düzlemdir. Bir yörünge düzlemini belirlemek için üç doğrusal nokta yeterlidir. Büyük bir cismin yörüngesinde hareket etmekte olan bir gökcisminin iki farklı zaman veya noktası bu ölçüme bir referans olabilir.
Laplace düzlemi veya Laplasyan düzlem, adını kaşifi Pierre-Simon Laplace'tan (1749-1827) alan ve bir gezegen uydusunun anlık yörünge düzleminin ekseni etrafında döndüğü ortalama ya da referans düzlemdir.















