
Coriolis kuvveti, dönen bir platformun merkezinden karşı tarafına yürümeye çalışan biri tarafından anlaşılabilir. Yürümek istediği tarafa doğru dik açıyla itildiğini görür. Benzer şekilde, dönen yer kürenin yüzeyi üzerinde hareket eden hava, kuzey yarım kürede hareket yönünün sağına, güney yarım kürede soluna saptırır. Bu saptırma gücüne coriolis kuvveti denir. Fransız matematikçi ve fizikçi Gaspard-Gustave Coriolis (1792-1843) onuruna atfen bu ad verilmiştir.

Publius Vergilius Maro, ünlü bir Romalı şairdir. Roma İmparatorluğu'nun destanı olarak kabul edilen Aeneis'in de yazarıdır.

Ambigram, diğer bir deyişle tersine çevirme (inversion), sunulduğu şekliyle okunabildiği gibi, tam tersine çevrildiğinde de okunabilen grafiksel figürlerdir. Douglas R. Hofstadter ambigramı "2 farklı okunuşu, birbirinin aynı eğrileri tıkıştırmak için yöneten bir kaligrafik dizayn" olarak tanımlamıştır. Ambigram sanatı ilk olarak kelimenin orijinini arkadaşına atfeden Hofstadter tarafından yayınlanmıştır. Hofstadter'in 1999 yayını Gödel, Escher, Bach kapakta 3 boyutlu bir ambigramı belirtiyordu.

Diferansiyel geometri türevin tanımlı olduğu Riemann manifoldlarının özellikleriyle uğraşan matematiğin bir alt disiplinidir. Başka bir deyişle, bu manifoldlar üzerindeki metrik kavramlarla uğraşır. Eğrilik, eğriler için burulma ve yüzeyler için değişik eğrilikler, araştırılan özellikler arasındadır.

Sarmal, burgu şekilli, üç boyutlu bir şekildir. Sarmal şekilli gündelik nesnelere örnek olarak silindirik yay, vida ve minare merdiveni gösterilebilir. Sarmallar biyolojide de yer alır, DNA molekülü birbirine sarılmış iki sarmaldan oluşur, çoğu proteinde de alfa sarmal olarak adlandırılan sarmal yapılar bulunur. Sıfat hali için sarmal kullanılır.

Başak Kümesi yaklaşık olarak 59 ± 4 milyon ışık yılı (18.0 ± 1.2 Mpc) uzaklıkta Başak takımyıldızında bulunan Gökada kümesi. Yaklaşık olarak 1300 (2000 ve üzeri de olabilir) gökada içerir Küme daha büyük olan Yerel süperküme'nin kalbini oluşturur ve Yerel grub'un uzak bir üyesidir. Kütlesi yaklaşık olarak 1.2×1015 M☉ olarak hesap edilir ve yarıçapı 2.2 milyon pc'dir.

Işık eğrisi, bir yıldızın veya bir bölgenin zamana karşı çizilen parlaklık grafiğidir.
Lucius Flavius Arrianus ve Nicomedia'lı Arrianus olarak bilinen Bitinya kökenli antik Romalı tarihçi,), yönetici, asker ve Roma ve Bizans dönemi filozofu. Büyük İskender ve onun doğu seferi hakkında en önemli kaynak Arrianus tarafından yazılan "Aleksandrou Anabasis" İskenderin Seferi adlı eseridir. Arrianos, İskender döneminde yaşamamış olmasına rağmen Büyük İskender'i takdir ettiğini sık sık yinelemektedir. "Aleksandrou Anabasis" adlı eseri, onun isminin ve yaptıklarının gelecek nesiller tarafından doğru bilinmesi için yazmıştır.

Eğri, matematikte doğruya benzer bir nesnedir. Ancak bunun doğrusal olması gerekmez.

Burt F. Bacharach Amerikalı bir piyanist, besteci ve müzik yapımcısı. Bacharach 1950'lerin ortalarından 1980'lerin ortalarına kadar seslendirdiği ve bestelediği hit şarkılarıyla bilinir. Bu şarkıların sözlerini Hal David yazmıştır. Birçok hit olmuş parçası Dionne Warwick tarafından seslendirilmiştir. Bacharach bu iş ortaklığının yakaladığı başarıyı fark etmiş ve bundan sonra Dusty Springfield, Bobbie Gentry, Jackie DeShannon ve diğer birçok sanatçıyla beraber birçok hit olmuş parça üretmiştir.

Roger Joseph Boscovich (Hırvatça: Ruđer Josip Bošković, Sırp-Hırvatça telaffuz: [rûd͡ʑer jǒsip bôʃkoʋit͡ɕ] ;, Ragusa'lı fizikçi, astronom, matematikçi, filozof, diplomat, şair, teolog, Cizvit rahip ve bilge

Spiral matematikte, bir merkez noktadan doğan, bu nokta etrafında dönerek kademeli olarak uzaklaşan bir eğridir.

Penguin Books Birleşik Krallık'ta kurulu bir yayınevidir. 1935 yılında Allen Lane tarafından The Bodley Head yayınevinin bir kolu olarak kurulmuş ve ertesi yıl bağımsız bir şirket olmuştur. Penguen yayınevi 1930'larda ucuz cep kitapları basarak ve bunları çeşitli zincir dükkanlarda geniş çaplı olarak dağıtarak kitap yayımcılığında çığır açmıştır. Penguin'in başarısı ciddi kitaplar için büyük kitlelerin ilgilendiğini göstermiştir. Penguen ayrıca siyaset, sanat ve bilim üzerine bastığı kitaplarla Birleşik Krallık'ta kamuoyunda etkili olmuştur.
Antakyalı Carpus eski bir Yunan matematikçi.
Eğri uydurma, muhtemelen kısıtlamalara tabi olan bir dizi veri noktasına en iyi uyan bir eğriyi veya matematiksel fonksiyonu oluşturma işlemidir. Yerleştirilen eğriler, veri görselleştirmeye yardımcı olarak, hiçbir veri bulunmadığında bir fonksiyonun değerlerini çıkarmak ve iki veya daha fazla değişken arasındaki ilişkileri özetlemek için kullanılabilir.
MacTutor Matematik Tarihi arşivi, John J. O'Connor ve Edmund F. Robertson tarafından sağlanan ve İskoçya'daki St Andrews Üniversitesi tarafından barındırılan bir web sitesidir. Birçok tarihsel ve çağdaş matematikçi hakkında ayrıntılı biyografilerin yanı sıra ünlü eğriler ve Matematik tarihindeki çeşitli konular hakkında bilgiler içerir.

Uzay ve zaman felsefesi, uzay ve zamanın ontolojisi, epistemolojisi ve karakterini çevreleyen konularla ilgilenen felsefe dalıdır.

Adolf Hitler tarafından yapılan konuşmalar listesi, Adolf Hitler'in yaptığı konuşmaları listeler. Hitler, 1919'da Münih'teki ilk konuşmasından, Şubat 1945'teki son konuşmasına kadar toplam 1525 konuşma yaptı. Bunların hepsini listelemek mümkün değildir, bu nedenle burada önemli konuşmalarından bazıları listelenmiştir.
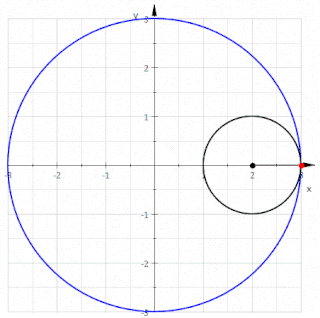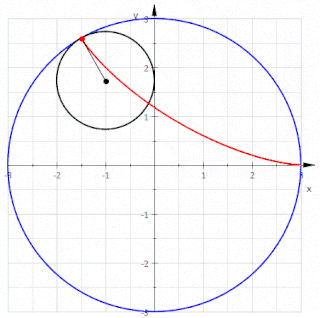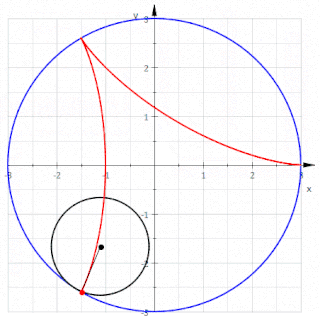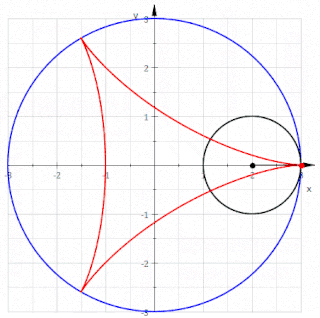
Geometride, triküspoid eğri veya Steiner eğrisi olarak da bilinen deltoid eğri, üç çentikten oluşan bir hiposikloiddir. Başka bir deyişle, bir çemberin çevresi üzerindeki bir noktanın, yarıçapının üç veya bir buçuk katı olan bir çemberin içinde kaymadan yuvarlanırken oluşturduğu yuvarlanma eğrisidir. Adını, benzediği büyük Yunanca delta (Δ) harfinden alır.
Bu, matematikte kullanılan eğrilerin Vikipedi makalelerine göre bir galerisidir. Ayrıca bakınız eğriler listesi.















