
Matematik'te aritmetiğin temel teoremi, aynı zamanda benzersiz çarpanlara ayırma teoremi ve asal çarpanlara ayırma teoremi olarak da adlandırılır, şunu belirtir: 1'den büyük her tamsayı, benzersiz bir şekilde asal sayıların üslerinin çarpımı olarak gösterilebilir.

Bir asal sayı, yalnızca 1'den büyük olup kendisinden küçük iki doğal sayının çarpımı olarak ifade edilemeyen bir doğal sayıdır. 1'den büyük ve asal olmayan doğal sayılara bileşik sayı adı verilir. Örneğin, 5 bir asal sayıdır çünkü onu bir çarpım olarak ifade etmenin mümkün olan yolları, 1 × 5 veya 5 × 1, yalnızca 5 sayısını içermektedir. Ancak, 4 bir bileşik sayıdır çünkü bu, her iki sayının da 4'ten küçük olduğu bir çarpım şeklindedir. Asal sayılar, aritmetiğin temel teoreminden ötürü sayı teorisi alanında merkezi öneme sahiptir: 1'den büyük her doğal sayı, ya bir asal sayıdır ya da asal sayıların çarpımı olarak, sıralamalarından bağımsız bir şekilde, benzersiz olarak çarpanlarına ayrılabilir.
P harfi "polynomial", NP harfleri ise "non-deterministic polynomial" ifadelerini temsil eder, Türkçe karşılıkları "polinom" ve "belirleyici olmayan polinom"dur. "P eşittir NP?" ise hesaplama teorisi'nin en temel ve meşhur problemidir.
Sözde rassal (rastgele) sayı üreteci, öğeleri arasında kolay kolay ilişki kurulamayacak bir sayı dizisi üreten algoritma türlerine verilen genel isimdir.
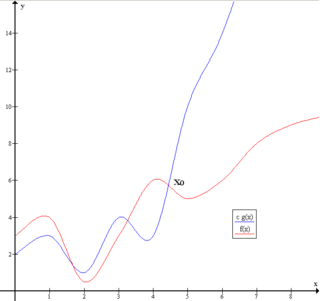
Büyük O (Big-Oh) gösterimi matematiksel bir gösterim olup işlevlerin (fonksiyonların) asimptotik davranışlarını tarif etmek için kullanılır. Bir işlevin büyümesinin asimptotik üst sınırını daha basit başka bir işlev cinsinden tanımlanması demektir. İki temel uygulama alanı vardır: matematik alanında genellikle kırpılmış bir sonsuz serinin kalan terimini karakterize etmek için kullanılır; bilgisayar bilimlerinde ise algoritmaların bilgi işlemsel karmaşıklığının çözümlemesi için kullanılır.
RSA, güvenliği tam sayıları çarpanlarına ayırmanın algoritmik zorluğuna dayanan bir tür açık anahtarlı şifreleme yöntemidir. 1978’de Ron Rivest, Adi Shamir ve Leonard Adleman tarafından bulunmuştur. Bir RSA kullanıcısı iki büyük asal sayının çarpımını üretir ve seçtiği diğer bir değerle birlikte ortak anahtar olarak ilan eder. Seçilen asal çarpanları ise saklar. Ortak anahtarı kullanan biri herhangi bir mesajı şifreleyebilir, ancak şu anki yöntemlerle eğer ortak anahtar yeterince büyükse sadece asal çarpanları bilen kişi bu mesajı çözebilir. RSA şifrelemeyi kırmanın çarpanlara ayırma problemini kırmak kadar zor olup olmadığı hala kesinleşmemiş bir problemdir.
Aşağıdaki tarihsel sıralama genel olarak algoritmaların ilk kökenlerinden başlayarak gelişimlerini ana hatlarıyla gösterir.
Matematikte, birkaç fonksiyon ya da fonksiyon gruplarının kendi isimleri yeterli öneme layıktır. Bu makaleler fonksiyonları açıklamak için olan daha ayrıntılı olarak gösteren bir listedir. İstatistik dışı ve matematiksel fizik gelişmeleri sonucu özel fonksiyonlar büyük bir teori olmuştur. Modern bir, soyut incelik fonksiyon uzayıları geniş karşılaştırma görünümü, sonsuz-boyutlu ve 'isimsiz' fonksiyonlar içindeki ve simetri ya da ilişki harmonik analiz ve grup temsilileri gibi özellikler ile özel fonksiyonlar ile seçilmiştir.
Rabin şifreleme sistemi, Rabin kriptoloji veya Rabin kriptosistemi, güvenliği RSA'daki gibi tam sayı çarpanlarına ayırmanın zorluğu üzerine kurgulanmış olan asimetrik bir kriptografik tekniktir. Bununla birlikte, Rabin kriptosisteminin avantajı, saldırgan tam sayıları verimli bir şekilde çarpanlarına ayıramadığı sürece, seçilmiş bir düz metin saldırısına karşı hesaplama açısından güvenli olduğu matematiksel olarak kanıtlanmıştır, oysa RSA için bilinen böyle bir kanıt yoktur. Rabin fonksiyonunun her çıktısının dört olası girdiden herhangi biri tarafından üretilebilmesi dezavantajı; her çıktı bir şifreli metinse, olası dört girdiden hangisinin gerçek düz metin olduğunu belirlemek için şifre çözmede ekstra karmaşıklık gerekir.
Sayı teorisinde, asal çarpanlara ayırma bir bileşik sayının, çarpıldıklarında yine aynı sayıyı verecek şekilde, bir ve kendisi dışındaki bölenlerine ayrılmasıdır.
Matematikte, özellikle soyut cebir ve uygulamalarında, ayrık logaritma, genel logaritmanın grup kuramındaki karşılığıdır. Genel olarak bakıldığında, loga(b) ifadesi, ax = b ifadesinin gerçel sayılar kümesi içindeki çözümlerine karşılık gelir. Benzer olarak, g ve h sonlu devirli grup G'nin elemanları olduğunda, gx = h ifadesinin çözümü olan x sonuçlarına h'nin g tabanındaki ayrık logaritması denir.

Çarpanlara ayırma, bir polinomun, tam sayının ya da matrisin kendisini oluşturan bileşenlerin çarpımı şeklinde yazılmasıdır. Örneğin 15 sayısı 3 ve 5 asal sayılarının çarpımı şeklinde yazılabilir: 3 × 5 ya da x2 − 4 polinomu (x − 2)(x + 2) şeklinde yazılabilir.
Goldwasser–Micali (GM) kriptosistemi 1982 yılında Shafi Goldwasser ve Silvio Micali tarafından geliştirilmiş bir asimetrik anahtar şifreleme algoritmasıdır. GM standart kriptografik varsayımlar altında güvenliği kanıtlanmış ilk probabilistik açık anahtar şifreleme yöntemidir. Bununla birlikte başlangıç düz metinden yüzlerce kez daha geniş olan şifreli metinler olduğundan verimli bir kriptosistem değildir. Kriptosistemin güvenlik özelliğini kanıtlamak için Shafi Goldwasser ve Silvio Micali anlamsal güvenliğin geniş alanda kullanılan bir tanımını önerdiler.

Eliptik Eğri Kriptolojisi, sonlu cisimler üzerindeki eliptik eğrilerin cebirsel topolojisine dayanan bir açık anahtar şifrelemesidir. Eliptik Eğri Kriptolojisi, diğer şifrelemeler göre daha küçük anahtar boyuna ihtiyaç duyar.
Sembolik matematik; sembolik hesaplama ve cebirsel hesaplamadan oluşan bilgisayar cebrindeki, matematiksel ifadeleri ve diğer matematiksel nesneleri manipüle etmek için kullanılan algoritma ve yazılımların çalışması ve geliştirilmesine atıfta bulunan bilimsel bir alandır.Daha açıkça ifade etmek gerekirse, bilgisayar cebri bilimsel hesaplamanın bir alt alanı sayılır ve bununla beraber bilimsel hesaplama genelde yaklaşık kayan nokta sayılarına ve sayısal yaklaşımlara dayanmaktadır.Buna karşın sembolik hesaplama, hiçbir değişkeni içermeyen ifadelerle tam hesaplamayı vurgulamaktadır.Değişken içermeyen ifadelere ilişkin semboller manipüle edilmektedir ve adı bundan dolayı sembolik matematik olarak kabul edilir.
Merkle imzası, anahtarlama ağaçları ve sayısal imza şemalarını birleştiren bir veri doğrulama yapısıdır. Özet değeri tabanlı kriptografidir ve Merkle ağacı da denen özet değeri ağacını kullanmaktadır. Verileri Lampart imza algoritması gibi tek kullanımlık şekilde imzalar. Ralph Merkle tarafından 1970 sonu itibarıyla geliştirilmiştir ve RSA, Dijital İmza Algoritması gibi geleneksel dijital imzalara alternatif olmuştur.
Bu, Wikipedia'da yer alan sayı teorisi konularıyla ilgili sayfaların bir listesidir.
Güçlü kriptografi veya kriptografik olarak güçlü, kriptografik sistemlere veya kriptanaliz için dirençli olduğu düşünülen bileşenlere uygulanan genel terimlerdir.

Teorik bilgisayar biliminde, zaman karmaşıklığı bir algoritma çalıştırmak için gereken bilgisayar zamanını tanımlayan hesaplama karmaşıklığıdır. Zaman karmaşıklığı genellikle algoritma tarafından gerçekleştirilen temel işlemlerin sayısı sayılarak ve her bir temel işlemin gerçekleştirilmesinin sabit bir zaman aldığı varsayılarak tahmin edilir. Böylece, algoritma tarafından gerçekleştirilen temel işlemlerin sayısı ile harcanan zamanın bir sabit faktör ile ilişkili olduğu kabul edilir.
Peter Williston Shor, MIT'de Amerikalı uygulamalı matematik profesörüdür. Kuantum hesaplama üzerine yaptığı çalışmalarla, özellikle de klasik bir bilgisayarda çalışan, şu anda bilinen en iyi algoritmadan katlanarak daha hızlı çarpanlara ayırmaya yönelik bir kuantum algoritması olan Shor algoritmasını geliştirmesiyle tanınır





