
Matematik ; sayılar, felsefe, uzay ve fizik gibi konularla ilgilenir. Matematikçiler ve filozoflar arasında matematiğin kesin kapsamı ve tanımı konusunda görüş ayrılığı vardır.

Matematik felsefesi, matematiğin varlıksal, bilgisel ve yöntemsel sorunlarını inceleyen, matematiğin temelleriyle ilgili ana kavramları irdeleyen bir felsefe dalıdır.
Matematik felsefesinin oluşturmacılık akımına göre matematiksel bir nesnenin varlığını kanıtlayabilmek için, nesnenin bulunması gerekir. Oluşturmacılara göre bir nesnenin var olmadığını varsayıp bu varsayımdan bir çelişki türetildiğinde -nesnenin kendisini bulmadıkça ("oluşturmadıkça")- nesnenin varlığı da kanıtlanmış olmaz.
Kategori teorisi ya da Ulam kuramı, matematiksel yapılar ve bunlar arasındaki ilişkilerle soyut olarak ilgilenen bir matematik kuramıdır. Kategori kuramı, öğelere (nesnelere) yoğunlaşan küme kuramının aksine, nesneler arası ilişkilere (morfizmlere) odaklanır.
Matematiğin temelleri olarak bilinen matematik dalı matematiğin tümü için geçerli olan en temel kavramları ve mantıksal yapıları inceler. Sayı, küme, fonksiyon, matematiksel tanıt, matematiksel tanım, matematiksel aksiyom, algoritma gibi kavramlar Matematiksel mantık, Aksiyomatik Küme Teorisi, Tanıtlama Teorisi, Model Teorisi, Hesaplama teorisi, Kategori Teorisi gibi yine matematiğim temelleri olarak anılan alanlarda incelenir. Bununla birlikte matematiğin temellerinin araştırılması matematik felsefesinin ana konularından biridir. Bu daldaki can alıcı soru matematiksel önermelerin hangi nihai esaslara göre "doğru" ya da "gerçek" kabul edilebileceğidir.

Matematiksel ispat, matematiksel bir ifade için türetilmiş varsayımların mantıksal olarak doğru olduğu sonucunu garantileyen, çıkarımsal bir argümandır. Argüman, teoremler gibi önceden oluşturulmuş diğer ifadeleri kullanabilir; lakin prensipte her delil, kabul edilen çıkarım kurallarıyla birlikte yalnızca aksiyom olarak bilinen belirli temel veya orijinal varsayımlar kullanılarak oluşturulabilir.

Ludwig Josef Johann Wittgenstein, Avusturya doğumlu filozof, matematikçi.
Matematiksel mantık, biçimsel mantığın matematiğe uygulanmasıyla ilgilenen bir matematik dalıdır. Metamatematik, matematiğin temelleri ve kuramsal bilgisayar bilimi alanlarıyla yakınlık gösterir. Matematiksel mantığın temel konuları biçimsel sistemlerin ifade gücünün ve biçimsel ispat sistemlerinin tümdengelim gücünün belirlenmesidir.
Teori veya kuram, bilimde bir olgunun, sürekli olarak doğrulanmış gözlem ve deneyler temel alınarak yapılan bir açıklamasıdır. Kuram, herhangi bir olayı açıklamak için kullanılan düşünce sistemidir. Genel anlamda kuram, bir düşüncenin genel, soyut ve ussal olmasıdır. Ayrıca bir kuram, açıklanabilir genel bağımsız ilkelere dayanmaktadır. Bu ilkelere bağlı kalarak doğada sonuçların nasıl örneklendirileceğini açıklamaya çalışır. Sözcüğün kökü Antik Yunan’dan gelmektedir. Ancak günümüzde birçok ayrı anlamlarda kullanılmaktadır. Kuram, varsayımla (hipotez) aynı anlama sahip değildir. İkisinin de anlamı başkadır. Kuram bir gözlem için açıklanabilir bir çerçeve sağlar ve kuramı sağlayacak olan sınanabilir varsayımlar tarafından desteklenir.

Mantık ya da eseme, bilginin yapısını inceleyen, doğru ile yanlış arasındaki akıl yürütmenin ayrımını yapan disiplindir, doğru düşüncenin aletidir. Önceleri bir felsefe dalıyken daha sonra kendi başına bir ihtisas alanı olmuştur. Matematik ve bilgisayar biliminin de parçası haline gelmiştir. Bir disiplin olarak Aristoteles tarafından kurulmuştur. Aristoteles'den etkilenen Farabi tarafından iki kısımda kategorize edilmiştir. İbn-i Sina geçicilik ve içerme arasındaki ilişkiyi geliştirmiştir. Çağdaş zamanlarda Frege, Russell ve Wittgenstein önemli katkılar yapmıştır.
Mantıkta, doğrulanabilir ya da yanlışlanabilir olmak zorunda olan ifadelere önerme denir. Kesin olan cümleler yanlış veya doğru da olsa önermedir; yani cümlenin yanlış veya doğru olduğunun bilinmesi gerekmez, doğrulanabilir olduğunun bilinmesi yeterlidir. Soru tümceleri önerme olamaz çünkü bir soru doğruluk ifade etmez.
Matematikte oluşturarak tanıtlama istenen özelliğe sahip somut bir örnek oluşturularak ya da böyle bir nesneyi oluşturma yöntemi verilerek, istenen özellikte bir matematiksel nesnenin var olduğunun tanıtlandığı bir yöntemdir. Bu yöntem, belirli özelliklere sahip olan matematiksel bir nesnenin var olduğunu tanıtlayan fakat bu nesnenin bir örneğini oluşturmak için yol göstermeyen oluşturmacı olmayan tanıtlama yöntemine karşıttır.
Çatışkı ya da Antinomi sözcük anlamı olarak iki yasanın gerçekte ya da görünüşte birbirleriyle uyuşmazlığıdır. Mantık ve epistemoloji’de geçen ve genel olarak bir paradoksu ya da çözümsüz bir çelişkiyi tanımlamak için kullanılan bir terimdir. Aynı anda ve ölçüde geçerli iki önermenin birbirinin yerine konulamazlığı durumunu ifade eder.

Sezgicilik ya da entüisyonizm, felsefi bir kavram olarak sezgiye akıl, zihin ve soyut düşünme karşısında hem öncelik hem de üstünlük tanıyan felsefe akımıdır. Henri Bergson akımın kurucusudur, bu nedenle kimi zaman felsefe tarihinde Bergsonculuk olarak adlandırılması da söz konusudur.

Sonsuz, eski Yunanca Lemniscate kelimesinden gelmektedir, çoğunlukla matematik ve fizikte herhangi bir sonu olmayan şeyleri ve sayıları tarif etmekte kullanılan soyut bir kavramdır.
Metaetik, etik anabilim dalının etik özelliklerinin, anlatım ve bildirimlerinin, tutumlarının ve yargılarının doğasını anlamak, arayıp bulmak ve ortaya çıkarmak maksadıyla uğraşan koludur.
Tarih boyunca matematiğin konu çeşitliliği ve derinliği artmaktadır, matematiği kavrama, birçok konuyu matematiğin daha genel alanlarına göre sınıflandırma ve düzenleme için bir sistem gerektirir. Bir dizi farklı sınıflandırma şeması ortaya çıkmıştır ve bazı benzerlikleri paylaşsalar da, kısmen hizmet ettikleri farklı amaçlara bağlı olarak farklılıkları vardır. Ek olarak, matematik geliştirilmeye devam ettikçe, bu sınıflandırma şemaları da yeni oluşturulan alanları veya farklı alanlar arasında yeni keşfedilen bağlantıları dikkate alacak şekilde değişmelidir. Farklı alanlar arasındaki sınırı aşan, genellikle en aktif olan bazı konuların sınıflandırılması daha zor hale gelir.
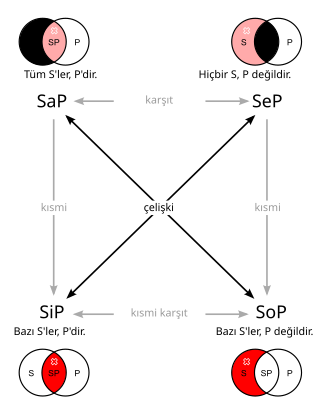
Klasik mantıkta, çelişki bir ya da daha fazla önerme arasında uyumsuzluk olması durumudur. Çelişkili iki önerme birlikte değerlendirildiğinde genellikle birbiriyle zıt olan iki mantıksal sonuç ortaya çıkar. Bu konuda Aristo'nun çelişmezlik kanunu'na göre "Aynı şey, aynı zamanda, aynı açıdan, aynı nesneye hem dahil hem de dahil olmayan olamaz"
Matematik, sayı, uzay, matematiksel yapı ve değişim gibi konuları araştıran bir çalışma alanıdır. Matematik ve bilim arasındaki ilişki hakkında daha fazla bilgi Matematik ve bilim bölümünde bulunabilir.
Matematikte, Alman matematikçi David Hilbert tarafından 1920'lerin başında formüle edilen Hilbert'in programı, matematiğin temellerini açıklığa kavuşturmaya yönelik ilk girişimlerin tutarsız olduğu bulunduğunda, matematiğin temel krizine önerilen bir çözümdü. Çözüm olarak Hilbert, mevcut tüm teorileri sonlu, sonlu bir aksiyom dizisine dayandırmayı ve bu aksiyomların tutarlı olduğuna dair bir kanıt sunmayı önerdi. Hilbert, gerçek analiz gibi daha karmaşık sistemlerin tutarlılığının daha basit sistemleri kullanarak kanıtlayabileceğini gösterdi.Sonuçta matematiğin tamamının tutarlılığı temel aritmetiğe indirgenebilir.





