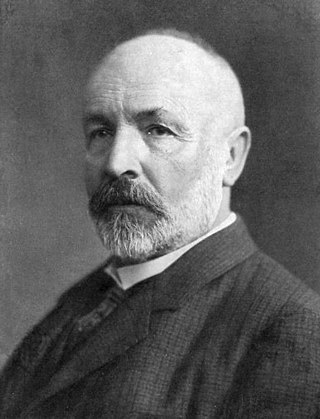Sayılabilir küme sonlu olan ya da doğal sayılarla birebir eşlenebilen kümelerin genel adıdır. Başka bir deyişle, eleman sayısı doğal sayılar kümesinden büyük olmayan kümeler sayılabilir olarak nitelenir.
| Sayılabilir küme |
|
|---|---|
| Kompozisyon cebiri |
|
| Split türleri |
|
| Diğer hiperkarmaşık sayılar |
|
| Diğer türler |
|
| İlgili diğer kavramlar |
|
Sayı, sayma, ölçme ve etiketleme için kullanılan bir matematiksel nesnedir. En temel örnek, doğal sayılardır. Sayılar, sayı adı (numeral) ile dilde temsil edilebilir. Daha evrensel olarak, tekil sayılar rakam adı verilen sembollerle temsil edilebilir; örneğin, "5" beş sayısını temsil eden bir rakamdır. Yalnızca nispeten az sayıda sembolün ezberlenebilmesi nedeniyle, temel rakamlar genellikle bir rakam sisteminde organize edilir, bu da herhangi bir sayıyı temsil etmenin organize bir yoludur. En yaygın rakam sistemi Hint-Arap rakam sistemidir, bu sistem on temel sayısal sembol, yani rakam kullanılarak herhangi bir negatif olmayan tam sayının temsil edilmesine olanak tanır. Sayılar sayma ve ölçme dışında, etiketlerde, sıralamada ve kodlarda kullanılmak için de sıklıkla kullanılır. Yaygın kullanımda, bir rakam ile temsil ettiği sayı net bir şekilde ayrılmaz.
Tam sayılar, sayılar kümesinde yer alan sıfır (0), pozitif yönde yer alan doğal sayılar ve bunların negatif değerlerinden oluşan negatif sayılardan oluşan sayı kümesidir.
Doğal sayılar, 
Geometri, matematiğin uzamsal ilişkiler ile ilgilenen alt dalıdır. Yunanca Γεωμετρία "Geo" (yer) ve "metro" (ölçüm) birleşiminden türetilmiş bir isimdir.
Matematikte reel sayılar kümesi, Fransızca réel “gerçek” den gelmektedir. Oranlı sayılar kümesinin evrim sürecinden elde edilen bir varsayım kombinasyonudur. Reel sayılar kümesi 
Georg Cantor'un doğal sayılar ile reel sayıların birebir eşlemesinin yapılamayacağını göstermek için geliştirdiği yöntem. Böyle bir eşlemenin yokluğu sonsuz elemanlı kümelerin büyüklüklerinin karşılaştırılması kavramının gelişimi açısından son derece önemlidir.
Sayılabilirlik, bir kümedeki eleman sayısıyla doğal sayılar arasında birebir eşleme kurulabilme durumu.
Ormancılık, ormanların ve ormanla ilişkili doğal kaynakların idaresi ağaçlandırma faaliyetleri ve bu faaliyetlerin yapılabilmesi için gerekli olan altyapı hizmetlerinin gerçekleştirildiği bir bilim dalı ve yönetim sanatıdır. Ormancılığın ana hedefi doğal kaynaklar ve hizmetlerin sürdürülebilirliğini sağlayacak sistemlerin oluşturulması ve geliştirilmesidir. Ormancılığın ana sorunsalı, toplumun ormanlardan karşılanan ihtiyaçlarının teminini sağlarken aynı zamanda orman kaynağının ve ormandan etkilenen diğer doğal kaynakların sağlıklı bir şekilde devamının sağlanabilmesidir.
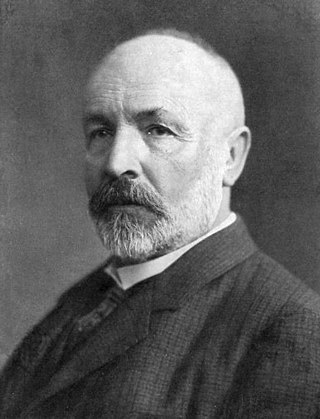
Georg Ferdinand Ludwig Philipp Cantor, Alman matematikçi. Kümeler kuramının kurucusudur. Kümeler arasında birebir eşlemenin önemini ortaya koydu, "sonsuz küme" kavramına matematiksel bir tanım getirdi ve gerçel sayıların sonsuzluğunun doğal sayıların sonsuzluğundan "daha büyük" olduğunu ispatladı. Ayrıca kardinal sayı ve ordinal sayı kavramlarını ortaya atmış ve bu sayıların aritmetiğini tanımlamıştır. Cantor'un buluşlarının matematik ve felsefede önemli yeri vardır.
Öge veya eleman, kümeler kuramında bir kümeye ait olan, fakat aynı zamanda tanımsız terimlerinden biridir. Kümelerin ya da genel olarak sınıfların ögesi olur.
Yıldız kümeleri veya yıldız bulutları, öz kütleçekimiyle bir arada tutulan büyük yıldız gruplarıdır. İki ana yıldız kümesi türü belirlenmiştir: Küresel kümeler, kütleçekimsel olarak bağlı on bin ila milyonlarca yaşlı yıldızın oluşturduğu sıkı gruplardır, açık kümeler ise genellikle birkaç yüzden az üye içeren, daha gevşek kümelenmiş ve çoğunlukla çok genç yıldızların oluşturduğu gruplardır. Açık kümeler, gökada içinde hareket ederken dev moleküler bulutların çekim etkisiyle zamanla dağılır, fakat küme üyeleri artık çekimsel olarak bağlı olmasalar da uzayda genel olarak aynı yönde hareket etmeye devam ederler; bunlara yıldız topluluğu, bazen de hareketli grup denir.
Dizi, bir sıralı listedir. Bir küme gibi, ögelerden oluşur. Sıralı ögelerin sayısına dizinin uzunluğu denir. Kümenin aksine sıralı ve aynı ögeler dizide farklı konumlarda birkaç kez bulunabilir. Tam olarak bir dizi, tanım kümesi sayılabilen toplam sıralı kümelerden oluşan bir fonksiyon olarak tanımlanabilir. Örneğin doğal sayılar gibi. Diziler bu örnekte olduğu gibi sonlu olabilir. Ya da tüm çift pozitif tam sayılar gibi sonsuz olabilir.
Matematikte, kardinal sayılar ya da nicel sayılar, kısaca kardinaller; bir kümenin kardinalitesi ya da nicesi olarak bilinen büyüklüğünü göstermek için kullanılan sayılardır. Sonlu kümelerde kardinalite, kümenin öğe sayısını gösteren doğal bir sayıdır. Sonsuz kümelerin öğe sayısını tanımlamak için transfinite kardinal sayılar vardır.
Küme, matematikte farklı nesnelerin topluluğu veya yığını olarak tanımlanmaktadır. Bu tanımdaki "nesne" soyut ya da somut bir şeydir. Fakat her ne olursa olsun iyi tanımlanmış olan bir şeyi, bir eşyayı ifade etmektedir. Örneğin, "Tüm canlılar topluluğu", "Dilimiz alfabesindeki harflerin topluluğu", "Masamın üzerindeki tüm kâğıtlar" tümcelerindeki nesnelerin anlaşılabilir, belirgin oldukları, kısaca iyi tanımlı oldukları açıkça ifade edilmektedir. Dolayısıyla bu tümcelerin her biri bir kümeyi tarif etmektedir. O halde, matematikte "İyi tanımlı nesnelerin topluluğuna küme denir." biçiminde bir tanımlama yapılmaktadır.
Sonsuz, eski Yunanca Lemniscate kelimesinden gelmektedir, çoğunlukla matematik ve fizikte herhangi bir sonu olmayan şeyleri ve sayıları tarif etmekte kullanılan soyut bir kavramdır.
Galaksi kümesi ya da gökada kümesi, kütle çekimi sayesinde birbirlerine bağlı yüzden fazla galaksinin oluşturduğu kümedir. Galaksi sayısı 50’nin altında olduğu zaman bu topluluklara, gruplar ve kümeler arasındaki sınırlar belirgin olmasa da, galaksi grubu denir. Galaksi kümeleri biçimleriyle dağılımlarıyla veya galaksi sayılarıyla nitelenirler. 10 milyar yıl önce oluştukları sanılmaktadır.
Sıra teorisi, ikili bağıntıları kullanma sırasının sezgisel kavramını inceleyen bir matematik dalıdır. "Bu, şundan daha küçüktür" veya "bu, şundan daha öncedir" gibi durumları inceler.
Açık yıldız kümeleri, birkaç bin yıldızdan oluşan bir yıldız grubudur. Açık yıldız kümesini oluşturan yıldızlar aynı dev moleküler buluttan oluşmuşlardır ve yaklaşık olarak aynı yaştadırlar. Açık yıldız kümesi galaktik küme olarak da bilinir. Samanyolu Galaksisi'nde 1100'den fazla açık yıldız kümesi keşfedilmiştir ve daha fazla olduğu düşünülmektedir. Açık yıldız kümeleri karşılıklı yerçekimi etkisiyle birbirlerine gevşek bir biçimde bağlıdırlar. Açık yıldız kümeleri diğer kümelerle ve gaz bulutlarıyla yakın temaslarda bulunarak bozulmuş hale gelirler. Bu bozulmalar hem galaksinin ana bölümüne doğru yer değiştirmelere hem de küme elemanlarının yakın temasların içine doğru kaybıyla sonuçlanır.
Alef sayıları, matematikte, daha ayrıntılı söylemek gerekirse kümeler teorisinde, iyi sıralı olabilen sonsuz kümelerin kardinalitesini göstermek için kullanılan sayılardır. Alef sayısı ismini sembolünden, İbranice alef harfinden alır. Bazı eski matematik kitaplarında yanlışlıkla alef sembolü ters basılmıştır.
Matematiksel analizde, küme üzerindeki bir ölçü, bu kümenin her bir uygun alt kümesine bir sayı atamanın sistematik bir yoludur ve sezgisel olarak kümenin boyutu olarak yorumlanır. Bu anlamda ölçü, uzunluk, alan ve hacim kavramlarının bir genellemesidir. Özellikle önemli bir örnek, Öklid geometrisinin geleneksel uzunluğunu, alanını ve hacmini n-boyutlu Öklid uzayının Rn uygun alt kümelerine atayan bir Öklid uzayındaki Lebesgue ölçüsüdür. Örneğin, gerçek sayılardaki [0, 1] aralığının Lebesgue ölçüsü, kelimenin günlük anlamındaki uzunluğudur ve tam olarak 1'dir.
