SHA-2
SHA-2, ABD Ulusal Güvenlik Ajansı (NSA) tarafından tasarlanmış kriptografik özet (hash) fonksiyonları kümesidir.[1] Kriptografik özet fonksiyonları, hesaplanmış “özet” (çalıştırılan algoritmanın çıktısı) ile bilinen ve beklenen özet değerinin karşılaştırılmasıyla, dijital veri üzerinde yürüyen matematiksel operasyonlardır. Özet fonksiyonları ile bir kişi verinin bütünlüğüne karar verebilir. Örneğin, yüklenmiş bir dosyanın özet değerini hesaplamak ve sonucu önceden açıklanmış özet sonucu ile karşılaştırmak, yüklemenin değiştirilip değiştirilmediğini veya üzerinde oynama yapılıp yapılmadığını gösterebilir.[2] Kriptografik Hash fonksiyonlarının kilit noktası çakışma dirençleridir: hiç kimse aynı özet çıktısı veren iki farklı girdi bulamamalıdır.
SHA-2, kendinden önce gelen SHA-1’den önemli farklılıklar içermektedir. SHA-2 ailesi basamakları (hash değerleri) 224, 256, 384 veya 512 bit olan altı hash fonksiyonundan oluşur: SHA-224, SHA-256, SHA-384, SHA-512, SHA-512/224, SHA-512/256, SHA-256 ve SHA-512 sırasıyla 32-bit ve 64-bitlik kelimelerle hesaplanmış orijinal özet fonksiyonlarıdır. Farklı kaydırma miktarları ve toplama sabitleri kullanırlar ancak yapıları neredeyse aynıdır. SHA-224 ve SHA-384 ilk ikisinin farklı başlangıç değerleri ile hesaplanmış, basitçe kesilmiş versiyonlarıdır. SHA-512/224 ve SHA-512/256 da SHA-512’nin kesilmiş versiyonlarıdır ama başlangıç değerleri Federal Bilgi İşleme Standardı (FIPS) PUB 180-4’te tanımlanmış metot kullanılarak üretilmiştir. SHA-2, Ulusal Standartlar ve Teknoloji Enstitüsü (NIST) bir Birleşik Devletler federal standardı (FIPS) tarafından 2001’de yayınlanmıştır. SHA-2 algoritmalar ailesi Birleşik Devletler 6829355 patentinde patentlenmiştir.[3] Birleşik Devletler patenti telifsiz lisans altında yayımlamıştır.[4]
2005’te, SHA-1 çakışmalarını, önceden mümkün olduğu düşünülen adım sayısından 2000 daha az adımda bulmak için bir algoritma geliştirilmiştir.[5] 2017’de SHA-1 çakışmasının bir örneği yayımlanmıştır.[6] SHA-1 tarafından bırakılan güvenlik marjini planlanandan zayıftır ve bu sebeple, kullanımı artık dijital imzalar gibi çakışma direncine bağımlı uygulamalar için önerilmemektedir. SHA-2, SHA-1 algoritmasına bazı benzerlikler taşısa da, bu ataklar SHA-2’ye başarılı bir şekilde genişletilememiştir.
Şu anda en iyi açık ataklar, aşağıda Kriptanaliz ve Doğrulama bölümünde gösterildiği gibi SHA-256’nın 52 turu veya SHA-512’nin 57 turu için preimage direncini ve SHA-256’nin 46 turu için çakışma direncini kırmaktadır.[7][8]
Özet (Hash) Standartları
FIPS PUB 180-2’nin yayımlanmasıyla, NIST SHA ailesinde üç tane ek özet fonksiyonu eklemiştir. Algoritmalar toplu olarak SHA-2 diye bilinir ve basamak uzunlukları (bit cinsinden) ile isimlendirilmişlerdir: SHA-256, SHA-384 ve SHA-512.
Algoritmalar ilk olarak 2001’de FIPS PUB 180-2 taslağında, public review and comments (kamu değerlendirmesi ve yorumları) kabul edildiğinde, yayımlanmışlardır. Ağustos 2002’de FIPS PUB 180-2, Nisan 1995’te yayımlanan FIPS PUB 180-1’in yerini alarak yeni Güvenli Hash Standardı haline geldi. Güncellenmiş standart, SHA-2 ailesinin iç çalışmalarını tanımlamasıyla tutarlı güncellenmiş teknik notasyonla birlikte orijinal SHA-1 algoritmasını içerir.[9]
Şubat 2004’te FIPS PUB 180-2 için, iki anahtarlı Üçlü DES’in anahtar uzunluğuyla eşleşmesi amacıyla SHA-224 için tanımlanmış ek bir değişkeni belirten bir değişiklik bildirimi yayımlandı.[10] Ekim 2008’de standart, FIPS PUB 180-3’te değişiklik bildirimindeki SHA-224 dahil olmak üzere güncellendi, ama bunun dışında standartta başka temel değişim yapılmadı. Standardı güncellemekteki başlıca motivasyon özet algoritmaları hakkındaki güvenlik bilgilerini ve Special Publications 800-107 ve 800-57 için kullanım önerilerini yeniden yerleştirmekti.[11][12][13] Detaylı test verisi ve örnek mesaj özetleri de standarttan kaldırıldı ve ayrı belge olarak temin edildi.[14]
Ocak 2011'de NIST,SP800-131A'yı yayınladı ve 2013 yılının sonuna kadar federal hükûmetin kullanımına izin verebilen 80 bit'lik (SHA-1 tarafından sağlanan) asgari güvenliğin 112 bitlik güvenlikle (SHA-2 tarafından sağlanan) değiştiğini belirtti. Yayın tarihinden itibaren minimum gereksinim ve önerilen güvenlik seviyesi bu şekilde değiştirildi.[15]
Mart 2012’de standart, SHA-512/224 ve SHA-512/256 özet fonksiyonları eklenerek ve SHA-512’nin kesilmiş versiyonları için başlangıç değerleri üretmek üzere bir metot tanımlanarak FIPS PUB 180-4’te güncellendi. Buna ek olarak, gerçek-zamanlı video veya ses beslemesi gibi özet verisinin içerik üretimi ile aynı anda hesaplanmasına izin verilerek, girdi verisini hash hesaplamasından önce eklemekteki kısıtlama kaldırıldı. Son veri bloğunu eklemek hala özet değeri çıktısından önce gerçekleştirilmelidir.[16]
Temmuz 2012’de NIST, kriptografik anahtar yönetimi için rehberlik sağlayan SP800-57’yi tekrar gözden geçirdi. Yayın, 2013’ten sonra özet güvenliği 112-bitten az olan dijital imzaların üretilmesine izin vermemektedir. 2007'den önceki revizyon, 2010'un sonuna kadar olan kesintiyi belirtti.[13] Ağustos 2012’de NIST, SP800-107’yi aynı şekilse gözden geçirdi.[12]
NIST özet fonksiyonu yarışması yeni hash fonksiyonu SHA-3’ü 2012 yılında seçti.[17] SHA-3 algoritması, SHA-2’den türetilmemiştir.
Uygulamalar
Daha fazla detay için kriptografik özet fonksiyonları başlığına bakabilirsiniz.
SHA-2 özet fonksiyonu, yaygın olarak kullanılan bazı güvenlik uygulamalarında ve protokollerde kullanılmaktadır, örneğin TLS ve SSL, PGP, SSH, S/MIME, and IPsec.
SHA-256, Debian yazılım paketleri[18] doğrulama sürecinde ve DKIM mesaj imzalama standardında yer almaktadır; SHA-256 and SHA-512'nin DNSSEC'de kullanılması önerilmektedir.[19] Unix ve Linux üreticileri, güvenli şifre özeti için 256-512 bit SHA-2'yi kullanmayı tercih etmektedir.[20]
Bitcoin gibi birkaç kripto para birimi işlemleri doğrulama yapmak, para iletimlerini kanıtlamak veya hisseleri hesaplamak için SHA-256 kullanır. ASIC SHA-2'nın çalışma hızındaki artış, kripto temelli ispat çalışmalarının daha fazla kullanılmasına neden oldu.
SHA-1 ve SHA-2, ABD'de bazı bölgelerde, kullanılması yasalar tarafından gerekli olan güvenli özet algoritmalarıdır. Başka şifreleme algoritmaları ve protokolleriyle birlikte devlet uygulamaları, hassas sınıflandırılmamış bilgilerin korunması için bu fonksiyonları kullanır. FIPS PUB 180-1, özel ve ticari kuruluşlar tarafından SHA-1'in benimsenmesini ve kullanılmasını teşvik etmiştir. Hükûmet, uygulamalarında SHA-1 kullanmayı bırakmaya başlamıştır. ABD Ulusal Standartlar ve Teknoloji Enstitüsü "Federal ajanslar, SHA-1 kullanmayı en kısa sürede çakışma direnci gerektiren uygulamalar için bırakmalı ve 2010'dan sonra bu uygulamalarda SHA-2 ailesi özet fonksiyonları kullanmalıdır" açıklamasında bulunmuştur.[21]
NIST'in bu açıklaması SHA-1'in bırakılma hızını arttırmıştır.[22]
SHA-2 fonksiyonları, SHA-1'den daha iyi güvenlik olmasına rağmen kabul edilme süreci hızlı değildi. Bu durumun nedenleri, Windows XP, SP2 veya daha üst sürümü çalıştıran sistemlerin SHA-2 için desteklenmemiş olması[23] ve henüz SHA-1 çakışmaları bulunmadığı için durumun acil olarak algılanamaması olabilir. Google Chrome ekibi, web tarayıcısının 2014'ün sonlarından 2015'in başlarına kadar bir süre boyunca SHA-1'e bağımlı TLS sertifikalarını kademeli olarak reddetmek için bir plan yaptıklarını açıkladı.[24][25][26] Benzer şekilde Microsoft,[27] Internet Explorer ve Edge'in kamuya açık SHA-1 imzalı TLS sertifikaları Şubat 2017'den itibaren onaylamayacağını açıkladı.
Kriptanaliz ve Doğrulama
Mesaj özetindeki bitlerin sayısının L olduğu bir özet fonksiyonu için belirli bir mesaj özetine karşılık gelen başka bir mesaj bulmak daima kaba kuvvet saldırısı (brute force attack) kullanılarak 2L hesaplamada yapılabilir. Buna saldırıya preimage attack denir. Saldırı L'ye ve hesaplamaların yapıldığı ortama bağlı olarak pratik olabilir ya da olmayabilir. İkinci kriterse aynı mesaj özetini üreten (çakışma olarak bilinen) collision iki farklı mesaj bulmamasıdır, doğum günü saldırısı (birthday attack) için ortalama sadece 2L/2 hesaplama gerektirir.
Şifre saklama işlemleri gibi kriptografik özetleri kullanan uygulamalar çakışma (collision) saldırısından en az etkilenirler. Belirli bir hesap için şifrenin oluşturulması, preimagesaldırılarını yanı sıra orijinal mesajın özet değerine(shadow dosyasında saklanmaktadır) erişimi gerektirir. Şifrelenmiş bir mesajın açılması bu saldırılarla mümkün değildir. Bununla birlikte en güvenli özet fonksiyonu bile zayıf parolalara karşı olan kaba kuvvet saldırılarını engellemez.
Belge imzalama durumlarında, bir saldırgan mevcut bir belge için basitçe sahte imza oluşturamaz; saldırganın zararsız ve zararlı olmak üzere iki adet belge üretmesi ve gizli anahtar sahibinin zararsız belgeyi imzalamasını istemesi gereklidir. Bunun mümkün olduğu bazı pratik koşullar vardır; 2008 yılının sonuna kadar, MD5 çakışmasıyla, yaygın olarak kullanılan web tarayıcıları tarafından kabul edilebilecek sahte SSL sertifikaları oluşturmak mümkündü.[28]
SHA-3 yarışması sırasında kriptografik özet analizine olan ilginin artması, SHA-2 ailesinde birkaç yeni saldırı ortaya çıkardı; bunların en iyileri aşağıdaki tabloda verilmiştir. Sadece çakışma saldırılarının karmaşıkları pratiktir; Saldırıların hiçbiri özet fonksiyonlarının tüm turları için geçerli değildir.
FSE 2012'de, Sony araştırmacıları sözde-çakışma saldırılarına karşı, SHA-256'nın 52 tura ve SHA-512'nin 57 tura uzatılmasını önerdi[29]
| Yayın yeri | Yıl | Saldırı Yöntemi | Saldırı | Versiyon | Tur | Karmaşıklık |
|---|---|---|---|---|---|---|
| New Collision Attacks Against Up To 24-step SHA-2[30] | 2008 | Deterministic | Çakışma | SHA-256 | 24/64 | 228.5 |
| SHA-512 | 24/80 | 232.5 | ||||
| Preimages for step-reduced SHA-2[31] | 2009 | Meet-in-the-middle | Preimage | SHA-256 | 42/64 | 2251.7 |
| 43/64 | 2254.9 | |||||
| SHA-512 | 42/80 | 2502.3 | ||||
| 46/80 | 2511.5 | |||||
| Advanced meet-in-the-middle preimage attacks[32] | 2010 | Meet-in-the-middle | Preimage | SHA-256 | 42/64 | 2248.4 |
| SHA-512 | 42/80 | 2494.6 | ||||
| Higher-Order Differential Attack on Reduced SHA-256[33] | 2011 | Differential | Sözde-Çakışma | SHA-256 | 46/64 | 2178 |
| 33/64 | 246 | |||||
| Bicliques for Preimages: Attacks on Skein-512 and the SHA-2 family[34] | 2011 | Biclique | Preimage | SHA-256 | 45/64 | 2255.5 |
| SHA-512 | 50/80 | 2511.5 | ||||
| Sözde-Çakışma | SHA-256 | 52/64 | 2255 | |||
| SHA-512 | 57/80 | 2511 | ||||
| Improving Local Collisions: New Attacks on Reduced SHA-256[35] | 2013 | Differential | Çakışma | SHA-256 | 31/64 | 265.5 |
| Sözde-Çakışma | SHA-256 | 38/64 | 237 | |||
| Branching Heuristics in Differential Collision Search with Applications to SHA-512[36] | 2014 | Heuristic differential | Sözde-Çakışma | SHA-512 | 38/80 | 240.5 |
| Analysis of SHA-512/224 and SHA-512/256[37] | 2016 | Differential | Çakışma | SHA-256 | 28/64 | practical |
| SHA-512 | 27/80 | practical | ||||
| Sözde-Çakışma | SHA-512 | 39/80 | practical |
Resmi Doğrulama
Ana makale: Cryptographic Module Validation Program
FIPS onaylı güvenlik işlevlerinin uygulamaları, Ulusal Standartlar Teknoloji Enstitüsü (NIST) ve Communications Security Establishment (CSE) ile ortaklaşa yürütülen CMVP programı aracılığıyla resmen doğrulanabilir. Gayri resmi doğrulama için NIST sitesinde, çok sayıda test vektörü üretmek içeren paketler, NIST'in sitesinde indirilebilir ancak bazı uygulamalar için sonuçta ortaya çıkan doğrulama, kanun tarafından gerekli görülen resmi CMVP doğrulamasının yerine geçmez.
Aralık 2013'ten itibaren, SHA-256'nın 1300'den ve SHA-512 'nin 900den fazla fazla geçerliliği varken yalnızca 5 tanesi mesajları her iki değişkene de destek verirken sekizin katı olmayan bit sayılarıyla çalışabilmektedir. (bkz. SHS Validation List 17 Haziran 2017 tarihinde Wayback Machine sitesinde arşivlendi.)
Test Değerleri
Boş stringlerin özet değerleri: (0 uzunluğundaki giriş metinlerinin).
SHA224("") 0x d14a028c2a3a2bc9476102bb288234c415a2b01f828ea62ac5b3e42f SHA256("") 0x e3b0c44298fc1c149afbf4c8996fb92427ae41e4649b934ca495991b7852b855 SHA384("") 0x 38b060a751ac96384cd9327eb1b1e36a21fdb71114be07434c0cc7bf63f6e1da274edebfe76f65fbd51ad2f14898b95b SHA512("") 0x cf83e1357eefb8bdf1542850d66d8007d620e4050b5715dc83f4a921d36ce9ce47d0d13c5d85f2b0ff8318d2877eec2f63b931bd47417a81a538327af927da3e SHA512/224("") 0x 6ed0dd02806fa89e25de060c19d3ac86cabb87d6a0ddd05c333b84f4 SHA512/256("") 0x c672b8d1ef56ed28ab87c3622c5114069bdd3ad7b8f9737498d0c01ecef0967a
Mesajdaki ufak bir değişiklik bile (çok büyük olasılıkla), avalanche effect(çığ etkisi) nedeniyle çok farklı bir özet oluşmasına sebep olacaktır. Örneğin, bu cümlenin sonuna bir nokta eklemek özet değerindeki bitlerinin neredeyse yarısını (224'ün 111'ü) değiştirir:
SHA224("The quick brown fox jumps over the lazy dog") 0x 730e109bd7a8a32b1cb9d9a09aa2325d2430587ddbc0c38bad911525 SHA224("The quick brown fox jumps over the lazy dog.") 0x 619cba8e8e05826e9b8c519c0a5c68f4fb653e8a3d8aa04bb2c8cd4c
Sözde Kodu
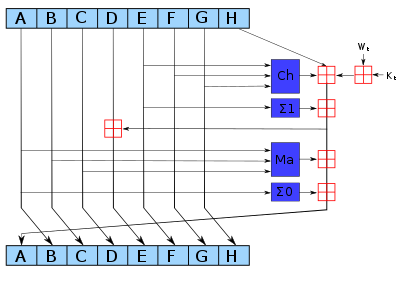
SHA-256 algoritması için sözde kod aşağıdaki gibidir. W [16..63] kelimelerinin bitleri arasındaki karıştırma işlemleri SHA-1'e kıyasla büyük oranda artmıştır.
Note 1: All variables are 32 bit unsigned integers and addition is calculated modulo 232 Note 2: For each round, there is one round constant k[i] and one entry in the message schedule array w[i], 0 ≤ i ≤ 63 Note 3: The compression function uses 8 working variables, a through h Note 4: Big-endian convention is used when expressing the constants in this pseudocode, and when parsing message block data from bytes to words, for example, the first word of the input message "abc" after padding is 0x61626380 Initialize hash values: (first 32 bits of the fractional parts of the square roots of the first 8 primes 2..19): h0 := 0x6a09e667 h1 := 0xbb67ae85 h2 := 0x3c6ef372 h3 := 0xa54ff53a h4 := 0x510e527f h5 := 0x9b05688c h6 := 0x1f83d9ab h7 := 0x5be0cd19 Initialize array of round constants: (first 32 bits of the fractional parts of the cube roots of the first 64 primes 2..311): k[0..63] := 0x428a2f98, 0x71374491, 0xb5c0fbcf, 0xe9b5dba5, 0x3956c25b, 0x59f111f1, 0x923f82a4, 0xab1c5ed5, 0xd807aa98, 0x12835b01, 0x243185be, 0x550c7dc3, 0x72be5d74, 0x80deb1fe, 0x9bdc06a7, 0xc19bf174, 0xe49b69c1, 0xefbe4786, 0x0fc19dc6, 0x240ca1cc, 0x2de92c6f, 0x4a7484aa, 0x5cb0a9dc, 0x76f988da, 0x983e5152, 0xa831c66d, 0xb00327c8, 0xbf597fc7, 0xc6e00bf3, 0xd5a79147, 0x06ca6351, 0x14292967, 0x27b70a85, 0x2e1b2138, 0x4d2c6dfc, 0x53380d13, 0x650a7354, 0x766a0abb, 0x81c2c92e, 0x92722c85, 0xa2bfe8a1, 0xa81a664b, 0xc24b8b70, 0xc76c51a3, 0xd192e819, 0xd6990624, 0xf40e3585, 0x106aa070, 0x19a4c116, 0x1e376c08, 0x2748774c, 0x34b0bcb5, 0x391c0cb3, 0x4ed8aa4a, 0x5b9cca4f, 0x682e6ff3, 0x748f82ee, 0x78a5636f, 0x84c87814, 0x8cc70208, 0x90befffa, 0xa4506ceb, 0xbef9a3f7, 0xc67178f2 Pre-processing: begin with the original message of length L bits append a single '1' bit append K '0' bits, where K is the minimum number >= 0 such that L + 1 + K + 64 is a multiple of 512 append L as a 64-bit big-endian integer, making the total post-processed length a multiple of 512 bits Process the message in successive 512-bit chunks: break message into 512-bit chunks for each chunk create a 64-entry message schedule array w[0..63] of 32-bit words (The initial values in w[0..63] don't matter, so many implementations zero them here) copy chunk into first 16 words w[0..15] of the message schedule array Extend the first 16 words into the remaining 48 words w[16..63] of the message schedule array: for i from 16 to 63 s0 := (w[i-15] rightrotate 7) xor (w[i-15] rightrotate 18) xor (w[i-15] rightshift 3) s1 := (w[i-2] rightrotate 17) xor (w[i-2] rightrotate 19) xor (w[i-2] rightshift 10) w[i] := w[i-16] + s0 + w[i-7] + s1 Initialize working variables to current hash value: a := h0 b := h1 c := h2 d := h3 e := h4 f := h5 g := h6 h := h7 Compression function main loop: for i from 0 to 63 S1 := (e rightrotate 6) xor (e rightrotate 11) xor (e rightrotate 25) ch := (e and f) xor ((not e) and g) temp1 := h + S1 + ch + k[i] + w[i] S0 := (a rightrotate 2) xor (a rightrotate 13) xor (a rightrotate 22) maj := (a and b) xor (a and c) xor (b and c) temp2 := S0 + maj h := g g := f f := e e := d + temp1 d := c c := b b := a Şablon:Not a typo := temp1 + temp2 Add the compressed chunk to the current hash value: h0 := h0 + a h1 := h1 + b h2 := h2 + c h3 := h3 + d h4 := h4 + e h5 := h5 + f h6 := h6 + g h7 := h7 + h Produce the final hash value (big-endian): digest := hash := h0 append h1 append h2 append h3 append h4 append h5 append h6 append h7
ch ve maj değerlerinin hesaplanması SHA-1 için anlatıldığı şekilde optimize edilebilir.
SHA-224 ile SHA-256 aşağıdaki maddeler haricinde aynıdır:
- İlk özet değeri
h0,h7'den farlıdır - Çıktı
h7atlanarak oluşturulmuştur.
SHA-224 initial hash values (in big endian): (The second 32 bits of the fractional parts of the square roots of the 9th through 16th primes 23..53) h[0..7] := 0xc1059ed8, 0x367cd507, 0x3070dd17, 0xf70e5939, 0xffc00b31, 0x68581511, 0x64f98fa7, 0xbefa4fa4
SHA-512 ile SHA-256 aşağıdaki maddeler haricinde yapı olarak aynıdır:
- Mesaj 1024-bitlik parçalara bölünmüştür,
- Başlangıç değerleri ve tur sabitleri 64 bite uzatılır,
- 64 yerine 80 tur vardır,
- Mesaj planlama dizisi w, 64 32-bit kelime yerine 80 64-bit kelime içerir,
- Mesaj planlama dizisi w'yi genişletmek için, döngü 16 ile 63 aralığında değil 16 ile 79 aralığında çalışır,
- Tur sabitleri ilk 80 asal sayıdır 2..409,
- Hesaplamalar için kullanılan kelime boyutu 64 bit uzunluğundadır,
- Mesajın uzatılmış uzunluğu (ön işleme tabi tutulmadan önce), 128 bitlik bir big-endian tam sayıdır,
- Kullanılan kaydırma ve tur sayıları farklıdır.
SHA-512 initial hash values (in big-endian): h[0..7] := 0x6a09e667f3bcc908, 0xbb67ae8584caa73b, 0x3c6ef372fe94f82b, 0xa54ff53a5f1d36f1, 0x510e527fade682d1, 0x9b05688c2b3e6c1f, 0x1f83d9abfb41bd6b, 0x5be0cd19137e2179 SHA-512 round constants: k[0..79] := [ 0x428a2f98d728ae22, 0x7137449123ef65cd, 0xb5c0fbcfec4d3b2f, 0xe9b5dba58189dbbc, 0x3956c25bf348b538, 0x59f111f1b605d019, 0x923f82a4af194f9b, 0xab1c5ed5da6d8118, 0xd807aa98a3030242, 0x12835b0145706fbe, 0x243185be4ee4b28c, 0x550c7dc3d5ffb4e2, 0x72be5d74f27b896f, 0x80deb1fe3b1696b1, 0x9bdc06a725c71235, 0xc19bf174cf692694, 0xe49b69c19ef14ad2, 0xefbe4786384f25e3, 0x0fc19dc68b8cd5b5, 0x240ca1cc77ac9c65, 0x2de92c6f592b0275, 0x4a7484aa6ea6e483, 0x5cb0a9dcbd41fbd4, 0x76f988da831153b5, 0x983e5152ee66dfab, 0xa831c66d2db43210, 0xb00327c898fb213f, 0xbf597fc7beef0ee4, 0xc6e00bf33da88fc2, 0xd5a79147930aa725, 0x06ca6351e003826f, 0x142929670a0e6e70, 0x27b70a8546d22ffc, 0x2e1b21385c26c926, 0x4d2c6dfc5ac42aed, 0x53380d139d95b3df, 0x650a73548baf63de, 0x766a0abb3c77b2a8, 0x81c2c92e47edaee6, 0x92722c851482353b, 0xa2bfe8a14cf10364, 0xa81a664bbc423001, 0xc24b8b70d0f89791, 0xc76c51a30654be30, 0xd192e819d6ef5218, 0xd69906245565a910, 0xf40e35855771202a, 0x106aa07032bbd1b8, 0x19a4c116b8d2d0c8, 0x1e376c085141ab53, 0x2748774cdf8eeb99, 0x34b0bcb5e19b48a8, 0x391c0cb3c5c95a63, 0x4ed8aa4ae3418acb, 0x5b9cca4f7763e373, 0x682e6ff3d6b2b8a3, 0x748f82ee5defb2fc, 0x78a5636f43172f60, 0x84c87814a1f0ab72, 0x8cc702081a6439ec, 0x90befffa23631e28, 0xa4506cebde82bde9, 0xbef9a3f7b2c67915, 0xc67178f2e372532b, 0xca273eceea26619c, 0xd186b8c721c0c207, 0xeada7dd6cde0eb1e, 0xf57d4f7fee6ed178, 0x06f067aa72176fba, 0x0a637dc5a2c898a6, 0x113f9804bef90dae, 0x1b710b35131c471b, 0x28db77f523047d84, 0x32caab7b40c72493, 0x3c9ebe0a15c9bebc, 0x431d67c49c100d4c, 0x4cc5d4becb3e42b6, 0x597f299cfc657e2a, 0x5fcb6fab3ad6faec, 0x6c44198c4a475817] SHA-512 Sum & Sigma: S0 := (a rightrotate 28) xor (a rightrotate 34) xor (a rightrotate 39) S1 := (e rightrotate 14) xor (e rightrotate 18) xor (e rightrotate 41) s0 := (w[i-15] rightrotate 1) xor (w[i-15] rightrotate 8) xor (w[i-15] rightshift 7) s1 := (w[i-2] rightrotate 19) xor (w[i-2] rightrotate 61) xor (w[i-2] rightshift 6)
SHA-384 ile SHA-521 aşağıdaki maddeler haricinde aynıdır:
- İlk özet değeri
h0,h7'den farlıdır - Çıktı h6 ve h7 atlanarak oluşturulmuştur.
SHA-384 initial hash values (in big-endian):
h[0..7] := 0xcbbb9d5dc1059ed8, 0x629a292a367cd507, 0x9159015a3070dd17, 0x152fecd8f70e5939,
0x67332667ffc00b31, 0x8eb44a8768581511, 0xdb0c2e0d64f98fa7, 0x47b5481dbefa4fa4
SHA-512/t ile SHA-512 aşağıdaki maddeler haricinde aynıdır:
- İlk özet değeri
h0danh7'ye SHA-512/t ilk değer oluşturma fonksiyonu tarafından üretilir. - Çıktı
h0ileh7arasındaki t bitlik kesişimden oluşur, - t 384'e eşit değildir, bunun yerine SHA-384 belirtildiği şekilde kullanılmalıdır.
- t değerlerinin 224 ve 256 onaylandığı özellikle belirtilmektedir.
SHA-512/t ilk değer üretme fonksiyonu değiştirilmiş SHA-512'yi ASCII dizesi "SHA-512 / t" üzerinden hesaplar, t ondalık gösteriminin yerini alır. Değiştirilmiş SHA-512 ile SHA-512 h0 h7 başlangıç değerleri, 0xa5a5a5a5a5a5a5a5 hexadecimal değeriyle XOR 'lanması dışında aynıdır.
SHA-2 ailesi karma işlevleri için örnek C uygulaması RFC 6234.'de bulunabilir
SHA Fonksiyonlarının Karşılaştırılması
Aşağıdaki tabloda, iç durum ; her bir veri bloğunun sıkıştırma işlemi sonundaki "iç özet değeri toplamı" dır.
Daha fazla bilgi için: Merkle–Damgård construction
| Algoritma ve çeşitleri | Çıktı boyutu (bitler) | İç durum boyutu (bitler) | Blok boyutu (bitler) | Maksimum mesaj boyutu (bitler) | Turlar | İşlemler | Güvenlik bitleri (Bilgi) | Örnek performans[39] (MiB/s) | İlk kez yayınlanışı | |
|---|---|---|---|---|---|---|---|---|---|---|
| MD5 (referans olarak) | 128 | 128 (4 × 32) | 512 | Limitsiz[40] | 64 | And, Xor, Rot, Add (mod 232), Or | <64 (çakışma bulundu) | 335 | 1992 | |
| SHA-0 | 160 | 160 (5 × 32) | 512 | 264 − 1 | 80 | And, Xor, Rot, Add (mod 232), Or | <80 (çakışma bulundu) | - | 1993 | |
| SHA-1 | 160 | 160 (5 × 32) | 512 | 264 − 1 | 80 | <63 (çakışma bulundu)[41] | 192 | 1995 | ||
| SHA-2 | SHA-224 SHA-256 | 224 256 | 256 (8 × 32) | 512 | 264 − 1 | 64 | And, Xor, Rot, Add (mod 232), Or, Shr | 112 | 139 | 2001 |
| SHA-384 SHA-512 SHA-512/224 SHA-512/256 | 384 512 224 256 | 512 (8 × 64) | 1024 | 2128 − 1 | 80 | And, Xor, Rot, Add (mod 264), Or, Shr | 192 256 112 128 | 154 | 2001 | |
| SHA-3 | SHA3-224 SHA3-256 SHA3-384 SHA3-512 | 224 256 384 512 | 1600 (5 × 5 × 64) | 1152 1088 832 576 | Limitsiz[42] | 24[43] | And, Xor, Rot, Not | 112 128 192 256 | - | 2015 |
| SHAKE128 SHAKE256 | d (isteğe bağlı) d (isteğe bağlı) | 1344 1088 | min(d/2, 128) min(d/2, 256) | - | 2015 | |||||
İşlemler sütununda, "Rot" rotate no carry, "Shr" ise right logical shift işlemlerini ifade eder.SHA-3 dışındaki algoritmaların hepsi, modüler toplama kullanır.
Yukarıdaki performans numaraları, 64-bit modunda Linux altında 2.2 GHz hızında çalışan ve yalnızca genel karşılaştırma için kaba bir nokta olarak sunulan bir AMD Opteron 8354 üzerinde tek parçacıklı bir uygulama içindir. Modern işlemci mimarileri üzerinde daha ayrıntılı performans ölçümleri aşağıdaki tabloda verilmiştir.
| İşlemci Mimarisi | Frekans | Algoritma | Kelime Uzunluğu (bit) | Döngü/byte x86 | MiB/s x86 | Döngü/byte x86-64 | MiB/s x86-64 |
|---|---|---|---|---|---|---|---|
| Intel Ivy Bridge | 3.5 GHz | SHA-256 | 32-bit | 16.80 | 199 | 13.05 | 256 |
| SHA-512 | 64-bit | 43.66 | 76 | 8.48 | 394 | ||
| AMD Piledriver | 3.8 GHz | SHA-256 | 32-bit | 22.87 | 158 | 18.47 | 196 |
| SHA-512 | 64-bit | 88.36 | 41 | 12.43 | 292 |
SHA-256, 32-bit hesaplamalar için tasarlandığı için x86 mimarisinde 64-bit işlemciler için optimize edilmiş koddan yararlanır.SHA-512'nin 32-bitlik uygulamaları 64-bitlik uygulamalarından önemli ölçüde yavaştır. Her iki algoritmanın farklı çıktı boyutlarına sahip varyantları, mesaj genişletme ve sıkıştırma fonksiyonları aynı olduğu ve yalnızca başlangıç özet değerlerinden dolayı çıktı boyutları farklı olduğu için benzer şekilde performans gösterecektir.MD5 ve SHA-1'in en iyi uygulamaları, modern işlemcilerde bayt başına 4,5 ila 6 devir arasında performans gösterir.
Testler Illinois Chicago Üniversitesi tarafından 3.5 GHz saat hızında bir Intel Xeon E3-1275 V2 çalıştıran hidra8 ve 3.8 GHz hızında bir AMD A10-5800K çalışan hydra9 sistemlerinde gerçekleştirildi.[44] Yukarıdaki Döngü/bayt hızları, SUPERCOP yazılımını kullanarak 4,096 baytlık bir mesajı işleyen bir algoritmanın performansıdır.[45] MiB / s performansı tek bir çekirdekteki CPU saat hızından çıkarılır; Gerçek dünyadaki performansı, çeşitli faktörlere bağlı olarak değişecektir.
Ayrıca bakınız
Kaynakça
- ^ "On the Secure Hash Algorithm family" 14 Ekim 2014 tarihinde Wayback Machine sitesinde arşivlendi. (PDF).
- ^ "Cryptographic Hash Function" 10 Temmuz 2017 tarihinde Wayback Machine sitesinde arşivlendi.. About.com
- ^ US 6829355
- ^ ""Licensing Declaration for US patent 6829355."". 16 Haziran 2016 tarihinde kaynağından arşivlendi. Erişim tarihi: 29 Nisan 2017.
- ^ "Schneier on Security: Cryptanalysis of SHA-1" 14 Nisan 2017 tarihinde Wayback Machine sitesinde arşivlendi.. Schneier.com.
- ^ Cryptology Group at Centrum Wiskunde & Informatica (CWI) and the Google Research Security, Privacy and Anti-abuse Group. "Shattered: We have broken SHA-1 in practice" 12 Nisan 2017 tarihinde Wayback Machine sitesinde arşivlendi.. SHAttered.
- ^ Dmitry Khovratovich, Christian Rechberger & Alexandra Savelieva (2011). "Bicliques for Preimages: Attacks on Skein-512 and the SHA-2 family" 22 Temmuz 2016 tarihinde Wayback Machine sitesinde arşivlendi. (PDF). IACR Cryptology ePrint Archive. 2011:286.
- ^ Mario Lamberger & Florian Mendel (2011). "Higher-Order Differential Attack on Reduced SHA-256" 29 Mart 2017 tarihinde Wayback Machine sitesinde arşivlendi. (PDF). IACR Cryptology ePrint Archive. 2011:37.
- ^ Federal Register Notice 02-21599, Announcing Approval of FIPS Publication 180-2 14 Mart 2022 tarihinde Wayback Machine sitesinde arşivlendi.
- ^ "FIPS 180-2 with Change Notice 1" 12 Mart 2012 tarihinde Wayback Machine sitesinde arşivlendi. (PDF). csrc.nist.gov
- ^ Federal Register Notice E8-24743, Announcing Approval of FIPS Publication 180-3
- ^ a b FIPS SP 800-107 Recommendation for Applications Using Approved Hash Algorithms 19 Mart 2013 tarihinde Wayback Machine sitesinde arşivlendi.
- ^ a b FIPS SP 800-57 Recommendation for Key Management: Part 1: General 26 Haziran 2013 tarihinde Wayback Machine sitesinde arşivlendi.
- ^ ""NIST.gov - Computer Security Division - Computer Security Resource Center"". 27 Mart 2016 tarihinde kaynağından arşivlendi. Erişim tarihi: 29 Nisan 2017.
- ^ FIPS SP 800-131A Recommendation for Transitioning the Use of Cryptographic Algorithms and Key Lengths 4 Eylül 2011 tarihinde Wayback Machine sitesinde arşivlendi.
- ^ Federal Register Notice 2012-5400, Announcing Approval of FIPS Publication 180-4
- ^ "NIST Selects Winner of Secure Hash Algorithm (SHA-3) Competition" 30 Nisan 2017 tarihinde Wayback Machine sitesinde arşivlendi.
- ^ "Debian codebase in Google Code". Google.
- ^ RFC 5702,RFC-Editor.org 21 Nisan 2017 tarihinde Wayback Machine sitesinde arşivlendi.
- ^ Ulrich Drepper, Unix crypt with SHA-256/512 18 Haziran 2010 tarihinde Wayback Machine sitesinde arşivlendi.
- ^ National Institute on Standards and Technology Computer Security Resource Center, NIST's Policy on Hash Functions 9 Haziran 2011 tarihinde Wayback Machine sitesinde arşivlendi.,
- ^ "Secure Hashing" 29 Nisan 2017 tarihinde Wayback Machine sitesinde arşivlendi.. NIST.
- ^ Microsoft Corporation,Overview of Windows XP Service Pack 3 17 Ocak 2009 tarihinde Wayback Machine sitesinde arşivlendi.
- ^ Chromium Blog, September 5, 2014, Gradually sunsetting SHA-1 13 Haziran 2015 tarihinde Wayback Machine sitesinde arşivlendi.
- ^ Eric Mill. "SHAAAAAAAAAAAAA" 1 Mart 2017 tarihinde Wayback Machine sitesinde arşivlendi.. SHAAAAAAAAAAAAA.com.
- ^ Filippo Valsorda, The Unofficial Chrome SHA1 Deprecation FAQ 30 Haziran 2017 tarihinde Wayback Machine sitesinde arşivlendi.
- ^ "An update to our SHA-1 deprecation roadmap - Microsoft Edge Dev BlogMicrosoft Edge Dev Blog 27 Haziran 2017 tarihinde Wayback Machine sitesinde arşivlendi.". blogs.windows.com.
- ^ Alexander Sotirov, Marc Stevens, Jacob Appelbaum, Arjen Lenstra, David Molnar, Dag Arne Osvik, Benne de Weger, MD5 considered harmful today: Creating a rogue CA certificate 25 Mart 2017 tarihinde Wayback Machine sitesinde arşivlendi., accessed March 29, 2009.
- ^ Ji Li, Takanori Isobe and Kyoji Shibutani, Sony China Research Laboratory and Sony Corporation, Converting Meet-in-the-Middle Preimage Attack into Pseudo Collision Attack: Application to SHA-2 4 Haziran 2016 tarihinde Wayback Machine sitesinde arşivlendi.
- ^ Somitra Kumar Sanadhya; Palash Sarkar (2008). "New Collision Attacks Against Up To 24-step SHA-2" (PDF). IACR Cryptology ePrint Archive. Cilt 2008:270. 22 Temmuz 2016 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 30 Nisan 2017.
- ^ Kazumaro Aoki; Jian Guo; Krystian Matusiewicz; Yu Sasaki; Lei Wang (2009). "Preimages for step-reduced SHA-2". Advances in Cryptology - ASIACRYPT 2009. Lecture Notes in Computer Science. Cilt 5912. Springer Berlin Heidelberg. ss. 578-597. doi:10.1007/978-3-642-10366-7_34. ISBN 978-3-642-10366-7. ISSN 0302-9743. 29 Haziran 2016 tarihinde kaynağından arşivlendi. Erişim tarihi: 30 Nisan 2017.
- ^ Jian Guo; San Ling; Christian Rechberger; Huaxiong Wang (2010). "Advanced meet-in-the-middle preimage attacks: First results on full Tiger, and improved results on MD4 and SHA-2" (PDF). Advances in Cryptology - ASIACRYPT 2010. Lecture Notes in Computer Science. Cilt 6477. Springer Berlin Heidelberg. ss. 56-75. doi:10.1007/978-3-642-17373-8_4. ISBN 978-3-642-17373-8. ISSN 0302-9743. 5 Mayıs 2012 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 30 Nisan 2017.
- ^ Mario Lamberger; Florian Mendel (2011). "Higher-Order Differential Attack on Reduced SHA-256" (PDF). IACR Cryptology ePrint Archive. Cilt 2011:37. 29 Mart 2017 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 29 Nisan 2017.
- ^ Dmitry Khovratovich, Christian Rechberger; Alexandra Savelieva (2011). "Bicliques for Preimages: Attacks on Skein-512 and the SHA-2 family" (PDF). IACR Cryptology ePrint Archive. Cilt 2011:286. 22 Temmuz 2016 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 29 Nisan 2017.
- ^ Florian Mendel; Tomislav Nad; Martin Schläffer (2013). "Improving Local Collisions: New Attacks on Reduced SHA-256". Advances in Cryptology – EUROCRYPT 2013. Lecture Notes in Computer Science. Cilt 7881. Springer Berlin Heidelberg. ss. 262-278. doi:10.1007/978-3-642-38348-9_16. ISBN 978-3-642-38348-9. ISSN 0302-9743. 6 Kasım 2018 tarihinde kaynağından arşivlendi. Erişim tarihi: 30 Nisan 2017.
- ^ Maria Eichlseder and Florian Mendel and Martin Schläffer (2014). "Branching Heuristics in Differential Collision Search with Applications to SHA-512" (PDF). IACR Cryptology ePrint Archive. Cilt 2014:302. 29 Haziran 2016 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 30 Nisan 2017.
- ^ Christoph Dobraunig; Maria Eichlseder; Florian Mendel (2016). "Analysis of SHA-512/224 and SHA-512/256" (PDF). 15 Temmuz 2017 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 30 Nisan 2017.
- ^ "Crypto++ 5.6.0 Benchmarks". 14 Ekim 2016 tarihinde kaynağından arşivlendi. Erişim tarihi: 13 Haziran 2013.
- ^ Found on an AMD Opteron 8354 2.2 GHz processor running 64-bit Linux[38]
- ^ "The MD5 Message-Digest Algorithm". 26 Nisan 2017 tarihinde kaynağından arşivlendi. Erişim tarihi: 18 Nisan 2016.
- ^ "Announcing the first SHA1 collision". 24 Nisan 2017 tarihinde kaynağından arşivlendi. Erişim tarihi: 23 Şubat 2017.
- ^ "The Sponge Functions Corner". 23 Ekim 2016 tarihinde kaynağından arşivlendi. Erişim tarihi: 27 Ocak 2016.
- ^ "The Keccak sponge function family". 6 Ağustos 2016 tarihinde kaynağından arşivlendi. Erişim tarihi: 27 Ocak 2016.
- ^ SUPERCOP Benchmarks Measurements of hash functions, indexed by machine 4 Aralık 2013 tarihinde Wayback Machine sitesinde arşivlendi.
- ^ "SUPERCOP".











