
Matematikte, diferansiyel denklem, bir ya da birden fazla fonksiyonu ve bunların türevlerini ilişkilendiren denklemdir. Fizik, kimya, mühendislik, biyoloji ve ekonomi alanlarında matematiksel modeller genellikle diferansiyel denklemler kullanılarak ifade edilirler. Bu denklemlerde, fonksiyonlar genellikle fiziksel ya da finansal değerlere, fonksiyon türevleriyse değerlerin değişim hızlarına denk gelir.

Johann Peter Gustav Lejeune Dirichlet, sayı teorisi ve Fourier serileri teorisi ile matematiksel analizdeki diğer konulara derin katkılarda bulunan Alman bir matematikçiydi. Bir fonksiyonun modern biçimsel tanımını veren ilk matematikçilerden biri olarak kabul edilmektedir.
Dirichlet problemi matematikte kısmi diferansiyel denklemler problemlerinde, çözümün verilen bir bölgede çözülmesi ile ilgilidir. Bu gerektirme Dirichlet limit şartı olarak bilinir.

Parabol, bir düzlemde alınan sabit bir "d" doğrusu ile sabit bir "F" noktasından eşit uzaklıktaki noktaların geometrik yerleştirilmesidir. Cebirde ise y=ax2+bx+c şeklindeki ikinci derece fonksiyonları grafiği olarak bilinir.
Matematikte, Laplace dönüşümü, zaman tanım kümesinde tanımlı bir fonksiyonu, frekans tanım kümesinde tanımlı bir başka fonksiyona dönüştürmek amacıyla kullanılır.
Schrödinger denklemi, bir kuantum sistemi hakkında bize her bilgiyi veren araç dalga fonksiyonu adında bir fonksiyondur. Dalga fonksiyonunun uzaya ve zamana bağlı değişimini gösteren denklemi ilk bulan Erwin Schrödinger’dir. Bu yüzden denklem Schrödinger denklemi adıyla anılır. 1900 yılında Max Planck'ın ortaya attığı "kuantum varsayımları"nın ardından, 1924'te ortaya atılan de Broglie varsayımı ve 1927'de ortaya atılan Heisenberg belirsizlik ilkesi bilim dünyasında yeni ufukların doğmasına sebep olmuştur. Bu gelişmeler Max Planck'ın kuantum varsayımları ve Schrödinger'in dalga mekaniği ile birleştirilerek kuantum mekaniğini ortaya çıkarmıştır.

Fizik, fiziksel kimya ve mühendislikte akışkanlar dinamiği, akışkanların akışını tanımlayan akışkanlar mekaniğinin bir alt disiplinidir. Aerodinamik ve hidrodinamik dahil olmak üzere çeşitli alt disiplinleri vardır. Akışkanlar dinamiğinin, uçaklardaki kuvvetlerin ve momentlerin hesaplanması, boru hatları boyunca petrolün Kütle akış hızının belirlenmesi, hava durumu modellerinin tahmin edilmesi, uzaydaki bulutsuların anlaşılması ve fisyon silahı patlamasının modellenmesi dahil olmak üzere geniş bir uygulama yelpazesi vardır.
Matematikte, bir kısmi diferansiyel denklem birkaç değişkenli bir fonksiyon ile bu fonksiyonun değişkenlere göre kısmi türevleri arasındaki ilişkiyi inceler.
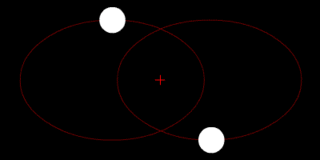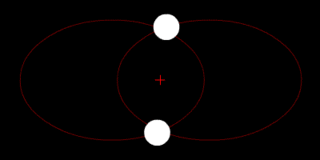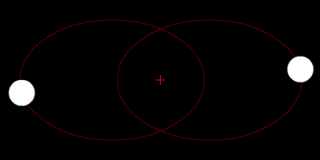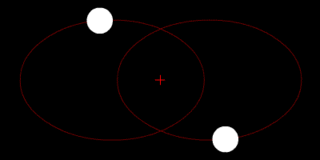
Klasik mekanikte iki cisim problemi sadece birbirleriyle etkileşen iki nokta parçacığın hareketini tanımlamak için kullanılır. Bir gezegen ve yörüngesinde dolanan bir uydu, bir yıldız ve yörüngesindeki bir gezegen, birbirlerinin yörüngelerinde dolanan iki yıldız ve klasik atom modelinde çekirdeğin etrafında dolanan elektron, yaygın örneklerdir.

Matematikte Laplace denklemi, özellikleri ilk defa Pierre-Simon Laplace tarafından çalışılmış bir kısmi diferansiyel denklemdir. Laplace denkleminin çözümleri, elektromanyetizma, astronomi ve akışkanlar dinamiği gibi birçok bilim alanında önemlidir çünkü çözümler bilhassa elektrik ve yerçekim potansiyeli ile akışkan potansiyelinin davranışını açıklar. Laplace denkleminin çözümlerinin genel teorisi aynı zamanda potansiyel teorisi olarak da bilinmektedir.

Matematiğin matematiksel fizik alanında ve rassal süreçler teorisinde bir harmonik fonksiyon, Rn'nin U gibi açık bir kümesi üzerinde f : U → R şeklinde tanımlı, Laplace denklemini, yani

Bessel fonksiyonları ilk önce Daniel Bernoulli tarafından tanımlanmış ve Friedrich Bessel tarafından genelleştirilmiş

Sayısal analiz, diğer adıyla nümerik analiz veya sayısal çözümleme, matematiksel analiz problemlerinin yaklaşık çözümlerinde kullanılan algoritmaları inceler. Bu nedenle birçok mühendislik dalı ve doğa bilimlerinde önem arz eden sayısal analiz, bilimsel hesaplama bilimi olarak da kabul edilebilir. Bilgisayarın işlem kapasitesinin artması ile gündelik hayatta ortaya çıkan birçok sistemin matematiksel modellenmesi mümkün olmuş ve sayısal analiz algoritmaları burada ön plana çıkmıştır. 21. yüzyıldan itibaren bilimsel hesaplama yöntemleri mühendislik ve doğa bilimleri ile sınırlı kalmamış ve sosyal bilimler ile işletme gibi alanları da etkilemiştir. Sayısal analizin alt başlıklarına adi diferansiyel denklemlerin yaklaşık çözümleri ve özellikle veri biliminde önem taşıyan sayısal lineer cebir ile optimizasyon örnek gösterilebilir.

Green fonksiyonları, matematikte homojen olmayan diferansiyel denklemlerin, istenen sınır koşulları altında çözülmesinde kullanılan bir yöntemi ve bu yöntemle ilişkili olarak hesaplanan fonksiyonu belirtmekte kullanılır. İlk kez matematikçi George Green tarafından kullanılmıştır.
Matematikte, Poisson denklemi elektrostatik, makine mühendisliği ve teorik fizik'de geniş kullanım alanına sahip eliptik türdeki Kısmi diferansiyel denklemlerdir. Fransız matematikçi, geometrici ve fizikçi olan Siméon Denis Poisson'dan sonra isimlendirilmiştir. Poisson denklemi

Değişken değiştirme, İntegral, çarpanlara ayırma, denklemler, üslü denklemler, trigonometri ve diferansiyel denklemler başta olmak üzere matematiğin her alanında işlemi basitleştirmek için kullanılan matematiksel bir yöntemdir.
Tam diferansiyel denklem veya Sağın diferansiyel denklem fizikte ve mühendislikte sıklıkla kullanılan bir tür adi diferansiyel denklemdir.
Floquet teorisi, periyodik katsayılı doğrusal diferansiyel denklem sistemlerinin çözümü ile ilgilenen bir matematik alt dalıdır. Floquet teorisi,





























