Sıfırın sıfırıncı kuvveti (00), sonucunun ne olduğu belirlenememiş matematiksel bir ifadedir. İfadenin sonucuna dair en yaygın iddialar sonucun 1 ya da belirsiz olduğu yönündedir. Cebir ve kombinatorikte genellikle sonucun 00 = 1 olduğu kabul edilirken, matematiksel analizde sonuç bazen tanımsız olarak gösterilir. Bilgisayar programları da bu ifadeyi farklı şekillerde çözmektedir.
Matematik ; sayılar, felsefe, uzay ve fizik gibi konularla ilgilenir. Matematikçiler ve filozoflar arasında matematiğin kesin kapsamı ve tanımı konusunda görüş ayrılığı vardır.
Matematik felsefesi, matematiğin varlıksal, bilgisel ve yöntemsel sorunlarını inceleyen, matematiğin temelleriyle ilgili ana kavramları irdeleyen bir felsefe dalıdır.
Matematiksel ispat, matematiksel bir ifade için türetilmiş varsayımların mantıksal olarak doğru olduğu sonucunu garantileyen, çıkarımsal bir argümandır. Argüman, teoremler gibi önceden oluşturulmuş diğer ifadeleri kullanabilir; lakin prensipte her delil, kabul edilen çıkarım kurallarıyla birlikte yalnızca aksiyom olarak bilinen belirli temel veya orijinal varsayımlar kullanılarak oluşturulabilir.
Matematiksel tümevarım bir önermenin, genellikle tüm doğal sayılar için ya da bazen sonsuz bir sıranın tüm elemanları için, doğru olduğunu göstermek üzere kullanılan bir matematiksel kanıtlama yöntemidir. Matematiksel mantık ve bilgisayar bilimlerinde kullanılan daha genel bir tanıtlama biçimi değerlendirilebilen (hesaplanabilen) ifadelerin denk olduğunu gösterir. Buna yapısal tümevarım denir.
Bilişim, bilişim bilimi ya da bilgisayar bilimi, bilgi ve hesaplamanın kuramsal temellerini ve bunların bilgisayar sistemlerinde uygulanabilmeleri sağlayan pratik teknikleri araştıran bir yapısal bilim dalıdır. Bilişimciler ya da bilgisayar bilimcileri bilgi oluşturan, tanımlayan ve dönüştüren algoritmik süreçler icat edip, kompleks sistemleri tasarlamak ve modellemek için uygun soyutlamalar formüle ederler. Bilişim Dünya'da hızla gelişmeye devam eden önemli bir teknolojidir.
Matematiksel mantık, biçimsel mantığın matematiğe uygulanmasıyla ilgilenen bir matematik dalıdır. Metamatematik, matematiğin temelleri ve kuramsal bilgisayar bilimi alanlarıyla yakınlık gösterir. Matematiksel mantığın temel konuları biçimsel sistemlerin ifade gücünün ve biçimsel ispat sistemlerinin tümdengelim gücünün belirlenmesidir.
Cebir sayılar teorisini, geometriyi ve analizi içine alan geniş bir matematik dalıdır. Temel matematik işlemlerinden, çember ve daire alanları bulmayı kapsayan geniş bir ilgi alanına sahiptir. Cebir, mühendislik ve eczacılık gibi birçok alanda kullanılmaktadır. Kuramsal cebir, ileri matematiğin bir dalı olmakla birlikte sadece uzmanlar tarafından çalışılan bir koldur.
Frekans veya titreşim sayısı bir olayın birim zaman içinde hangi sıklıkla, kaç defa tekrarlandığının ölçümüdür, matematiksel ifadeyle çarpmaya göre tersi ise periyot olarak adlandırılır.
İstatistik veya sayım bilimi, belirli bir amaç için veri toplama, tablo ve grafiklerle özetleme, sonuçları yorumlama, sonuçların güven derecelerini açıklama, örneklerden elde edilen sonuçları kitle için genelleme, özellikler arasındaki ilişkiyi araştırma, çeşitli konularda geleceğe ilişkin tahmin yapma, deney düzenleme ve gözlem ilkelerini kapsayan bir bilimdir. Belirli bir amaç için verilerin toplanması, sınıflandırılması, çözümlenmesi ve sonuçlarının yorumlanması esasına dayanır. Bu çerçevede yapılan işlemlerin tümüne sayımlama denir.
Jacob Bernoulli, Bernoulli ailesindeki ünlü matematikçilerden biridir. Leibniz kalkülüsünün ilk savunucularındandır ve Leibniz- Newton kalkülüs tartışmasında Leibniz'in yanında yer almıştır. Kardeşi Johann Bernoulli ile kalkülüse yaptığı birçok katkıyla da ünlüdür. Ancak, matematiğe en önemli katkısı büyük sayılar yasası ile olasılık alanında olmuştur.
Koreografi, adım tasarımcılığı, dans besteciliğidir. Kelime Yunancadan gelir. Antik Yunan tiyatrosunda koroda bulunan insanların hareketlerini belirleme şeklinde ortaya çıkmıştır. Daha sonra dans esnasında adım ve hareketleri belirleme şekline dönüşmüş ve bu şekilde yaygınlaşmıştır. Bu işi yapanlara koreograf denir.
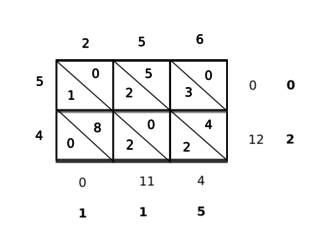
Çarpma, temel aritmetik işlemlerden biridir. Sayılarda çarpma, çarpılan sayının çarpan sayı kadar adedinin toplamının alınması işlemidir.
Matematik bilimi içinde moment kavramı fizik bilimi için ortaya çıkartılmış olan moment kavramından geliştirilmiştir. Bir bir reel değişkenin reel-değerli fonksiyon olan f(x)in c değeri etrafında ninci momenti şöyle ifade edilir:
Olasılık kuramı bilim dalında matematiksel beklenti veya beklenen değer veya ortalama birçok defa tekrarlanan ve her tekrarda mümkün tüm olasılıklarını değiştirmeyen rastgele deneyler sonuçlarından beklenen ortalama değeri temsil eder. Bir ayrık rassal değişkennin alabileceği bütün sonuç değerlerin olasılıklarıyla çarpılması ve bu işlemin bütün değerler üzerinden toplanmasıyla elde edilen değerdir. Bir sürekli rassal değişken için rassal değişken ile olasılık yoğunluk fonksiyonunun çarpımının aralığı belirsiz integralidir. Fakat dikkat edilmelidir ki bu değerin genel pratik anlamla rasyonel olarak beklenmesi pek uygun olmayabilir, çünkü matematiksel beklentiin olasılığı çok düşük belki sıfıra çok yakın olabilir ve hatta pratikte matematiksel beklenti bulunmaz. Ağırlıklı ortalama olarak da düşünülebilir ki değerler ağırlık katsayıları verilen olasılık kütle fonksiyonu veya olasılık yoğunluk fonksiyonudur.
Bir matematiksel gösterim, matematiksel nesne ve fikirlerin sembolik temsillerinin bir sistemdir. Matematiksel gösterimler, fiziksel bilimler, mühendislik ve ekonomi bilimi ve matematikte kullanılır. Matematiksel gösterimler ilgili basit sembolik temsilleri içerir, örneğin; sayılar 1 ve 2, fonksiyonel semboller; sin ve +; kavramsal semboller, örneğin; lim, dy/dx, denklemler ve değişkenler; ve kompleks diyagramatik gösterimler örneğin; Penrose grafiksel gösterimi ve Coxeter-Dynkin diyagramları.
Matematiksel model, bir sistemin matematiksel kavramlar ve dil kullanılarak tanımlanmasıdır. Matematiksel model geliştirme süreci, matematiksel modelleme olarak adlandırılır. Matematiksel modeller, doğa bilimlerinde ve mühendislik disiplinlerinde bunun yanı sıra sosyal bilimlerde kullanılır. Matematiksel modelleri daha çok fizikçiler, mühendisler, istatistikçiler, operasyon araştırma analistleri ve ekonomistler kullanır. Model, bir sistemi açıklamaya, farklı bileşenlerin etkilerini incelemeye ve bir davranış hakkında öngörüde bulunmak için yardımcı olabilir.
Kalkülüs ve matematiksel analizin diğer dallarında cebirsel işlemlerle ilgili olan limitler, daha çok alt ifadelerin yer değiştirmesi ile gerçekleştirilir. Bu değişimden sonra elde edilen ifade eğer, asıl limit ile ilgili yeteri kadar bilgi içermiyorsa, buna 'belirsiz form denir.
Sembolik matematik; sembolik hesaplama ve cebirsel hesaplamadan oluşan bilgisayar cebrindeki, matematiksel ifadeleri ve diğer matematiksel nesneleri manipüle etmek için kullanılan algoritma ve yazılımların çalışması ve geliştirilmesine atıfta bulunan bilimsel bir alandır.Daha açıkça ifade etmek gerekirse, bilgisayar cebri bilimsel hesaplamanın bir alt alanı sayılır ve bununla beraber bilimsel hesaplama genelde yaklaşık kayan nokta sayılarına ve sayısal yaklaşımlara dayanmaktadır.Buna karşın sembolik hesaplama, hiçbir değişkeni içermeyen ifadelerle tam hesaplamayı vurgulamaktadır.Değişken içermeyen ifadelere ilişkin semboller manipüle edilmektedir ve adı bundan dolayı sembolik matematik olarak kabul edilir.
2015 Ceylanpınar saldırısı, 22 Temmuz 2015 günü Şanlıurfa'nın Ceylanpınar ilçesinde gerçekleşen 2 polisin ölümüyle sonuçlanan saldırı.
Türev işareti, bir sayının veya bir cebirsel ifadenin türevini aldıran matematiksel bir işarettir.