Matematikte cebirin temel teoremi karmaşık değişkenli polinomların köklerinin varlığıyla ilgili temel bir sonuçtur. D'Alembert-Gauss teoremi olarak da anılmaktadır.
Türev, matematikteki ve özellikle diferansiyeldeki temel kavramlardan biridir. Aşağıda temel türev alma kuralları ve bazı fonksiyonların türev kuralları yer almaktadır.
Matematikte, bir polinom belirli sayıda bağımsız değişken ve sabit sayıdan oluşan bir ifadedir. Polinom kendi içinde toplama, çıkarma, çarpma ve negatif olmayan sayının üssünü alma işlemlerini kullanır. Örnek olarak tek bilinmeyenli bir polinom olan x2 − 4x + 7, ikinci dereceden oluşan bir polinomdur. Diğer bir örnek olarak, x2 − 4/x + 7x3/2 bir polinom değildir, çünkü polinomlarda terimlerin derecelerinin doğal sayı olma zorunluluğu vardır 2. terimde x′i ele alan bir bölme işlemi x'in derecesini negatif yapmaktadır ve 3. terim doğal sayı olmayan bir derece içermektedir (3/2).
e sayısı veya Euler sayısı, matematik, doğal bilimler ve mühendislikte önemli yeri olan sabit bir reel sayı, doğal logaritmanın tabanı. e sayısı aşkın bir sayıdır, dolayısıyla irrasyoneldir ve tam değeri sonlu sayıda rakam kullanılarak yazılamaz. Yaklaşık değeri şöyledir:
Matematikte, Fourier serileri bir periyodik fonksiyonu basit dalgalı fonksiyonların toplamına çevirir.
Gauss integrali, Euler–Poisson integrali olarak da bilinir, tüm reel sayılardaki e−x2 Gauss fonksiyonunun integralidir. Alman matematik ve fizikçi Carl Friedrich Gauss'dan sonra adlandırlıdı. İntegrali şöyledir:
Matematik'te, digama fonksiyonu gama fonksiyonu'nun logaritmik türevi olarak tanımlanır:
Matematik'te, Turán eşitsizliği Paul Turán tarafından Legendre polinomu'larının genellemesi için bulundu. (ilk yayınlanması Szegö ) tarafından oldu.Başka diğer polinomlar içinde birçok genellemeler Turán eşitsizliği ile verilir.
Laguerre polinomları, matematikte adını Edmond Laguerre'den almıştır. Kanonik (benzer) adlandırma Laguerre denklemi'dir:
Matematik'te, Hurwitz zeta fonksiyonu, adını Adolf Hurwitz'ten almıştır, çoğunlukla zeta fonksiyonu denir. Formel tanımı için kompleks değişken s 'in Re(s)>1 ve q 'nun Re(q)>0 yardımıyla
Matematikte, a Neumann polinomali,Carl Neumann tarafından özel durum 
için sunulan, Bessel fonksiyonu terimleri içerisinde fonksiyonların 1/z açılımında kullanılan bir polinomdur.
Matematiksel analizde Legendre fonksiyonları, aşağıdaki Legendre diferansiyel denkleminin çözümleridir.
; 
Jacobi sembolü Legendre sembolünün bir genellemesidir. 1837 yılında Jacobi tarafından tanıtılan bu teori, modüler aritmetik ve sayılar teorisinin diğer dallarındandır ama ana kullanımı hesaplamada sayılar teorisi, özellikle asallık testi ve tam sayıları çarpanlara ayırma olarak kriptografide oldukça önemlidir.
Kuantum harmonik salınıcı, klasik harmonik salınıcın benzeşiğidir. Rastgele seçilmiş potansiyeli denge noktası civarında harmonik potansiyele yakınsanabildiğinden nicem mekanğindeki en önemli model sistemlerden biridir. Dahası, nicem mekaniğinde kesin analitik çözümü olan çok az sistemden biridir.
Askey-Gasper eşitsizliği, Richard Askey ile George Gasper tarafından 1976'da ispatlanan, bir Jacobi polinomu eşitsizliğidir. Bieberbach varsayımının kanıtlanmasında kullanılmıştır.
Matematikte, küresel harmonikler Laplace denkleminin çözüm kümesinin açısal kısmıdır. Küresel koordinatların bir sistemi içinde küre yüzeyinde tanımlanır, Fourier serisi ise çember üzerinde tanımlanır. Laplace'ın küresel harmonikleri 
Pierre Simon de Laplace tarafından ilk 1782 yılında tanıtılan bir ortogonal sistemin küresel harmonik formlarının özel bir kümesidir. Küresel harmoniklerden birkaçının kökleri sağda gösterimlenmiştir. Küresel harmonikler pek çok yerde teorik önem taşımaktadır ve özellikle atomik yörünge elektron konfigürasyonları, yerçekimi alanları, geoitleri ve gezegen ve yıldızların manyetik alanlarının temsili ve kozmik mikrodalga arka plan radyasyonu karakterizasyonu hesaplanmasında kullanılan pratik uygulamaları vardır. Küresel harmonikler 3D Bilgisayar grafiklerinde, dolaylı aydınlatma ve 3D şekillerin tanınması gibi konularda geniş bir yelpazede özel bir rol oynamaktadır.
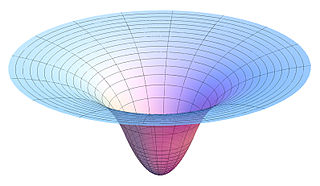
Klasik mekanikte, bir yerdeki yerçekimi potansiyeli iş bölü birim ağırlığa eşittir. Sabit bir referans noktası için bir nesnenin yerçekimi kuvveti tarafından oluşan hareketidir. Yük rolü oynayan bir ağırlığın elektrik potansiyeline benzerdir. Referans noktasında potansiyel herhangi bir ağırlığın sonsuz uzaklıkta toplanmasından dolayı 0'dır ve sonlu bir uzunlukta negatif bir potansiyelle sonuçlanır. Matematikte, yerçekimi potansiyeli ayrıca Newton potansiyeli olarak bilinir ve potansiyel teorinin çalışmasının temelidir.
Hermit polinomları, 1810'da Pierre-Simon Laplace tarafından tanımlanmış, ancak pek tanınmayan bir biçimde 1859'da Pafnuty Chebyshev tarafından ayrıntılı olarak incelenmiştir. Chebyshev'in çalışması gözden kaçmış ve daha sonra 1864'te polinomlar üzerine yazan ve onları yeni olarak tanımlayan Charles Hermite'nin adıyla anılmışlardır. Sonuç olarak yeni değillerdi, ancak Hermite 1865'teki yayınlarında çok boyutlu polinomları tanımlayan ilk kişi olmuştur.
Matematikte Euler sayıları, Taylor serisi açılımıyla tanımlanan bir En tam sayı dizisidir..
Bessel polinomları, matematikteki ortogonal polinomların bir dizisidir. Bessel polinomlarıyla ilgili birbirinden farklı ama birbiriyle yakından ilişkili çok sayıda tanım vardır. Matematikçiler tarafından tercih edilen tanım şu seriyle verilmektedir:
![{\displaystyle P_{n}(x)={1 \over 2^{n}n!}{d^{n} \over dx^{n}}\left[(x^{2}-1)^{n}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9414fbe11099d281205ca2a2f051f405c2d348c)
![{\displaystyle p_{n}(x)={\frac {1}{{e_{n}}W(x)}}\ {\frac {d^{n}}{dx^{n}}}\left(W(x)[Q(x)]^{n}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e1fa10228acf263d27254a5717ba52519dba2d1)
