
Bir üçgen düzlemde birbirine doğrusal olmayan üç noktayı birleştiren üç doğru parçasının birleşimidir. Üçgene müselles ve üçbucak da denir.

Henri Léon Lebesgue, 17. yüzyıl integral kavramının-bir eksen ile o eksen için tanımlanmış bir fonksiyonun eğrisi arasındaki alanı toplamak- bir genellemesi olan entegrasyon teorisi ile tanınan Fransız matematikçiydi. Teorisi ilk olarak 1902'de Nancy Üniversitesi'ndeki Intégrale, longueur, aire tezinde yayınlandı.
Matematikte cebirsel uzam bilgisinde Max Noether teoremi, Max Noether'in en az altı kuramına işâret edebilir. Noether teoremiyle genelde kızı Emmy Noether'in bir çalışmasıyla bulduğu sonuç adlandırılmaktadır.
- Max Noether artık kesişim teoremi (Fundamentalsatz veya temel teorem, izdüşümsel düzlemde cebirsel eğriler üzerinde artık kümelerin kesişiminden elde edilmiş bir sonuçtur.
- Cebirsel yüzeyler için bulunan Max Noether teoremi, aşırıyüzeylerde P3'de bulunan ya da daha genel olarak tam kesişmeler yapan eğrileri konu alır.
- Bir Kuramsal eğriler üzerine Max Noether teoremi' vardır.
- Yüzeylerin rasyonelliği üzerine Noether teoremi bulunmaktadır.
- Kremona grubu'nu ikincil dönüştürmelerle oluşturma üzerine bir Max Noether teoremi mevcuttur.
- İkincil diferansiyellerin bir eğri üzerinde oluşturulması üzerine bir Max Noether teoremi vardır ki bu teorem, Abelyen diferensiyelleri, genus'ları > 2 olan ve aşırıeliptik eğri olmayan eğriler için kullanır.

Karmaşık analiz ya da başka bir deyişle kompleks analiz, bir karmaşık değişkenli fonksiyonları araştıran bir matematik dalıdır. Bir değişkenli karmaşık analize ya da çok değişkenli karmaşık analizle beraber tümüne karmaşık değişkenli fonksiyonlar teorisi de denilir.
Ana başlıklarına göre karmaşık analiz konuları:
Karmaşık analizde, tam fonksiyon veya başka bir deyişle integral fonksiyonu, karmaşık düzlemin tümünde holomorf olan karmaşık değerli bir fonksiyondur. Tam fonksiyonların tipik örnekleri polinomlar, üstel fonksiyon ve bunların toplamları, çarpımları ve bileşkeleridir. Her tam fonksiyon tıkız kümeler üzerinde düzgün bir şekilde yakınsayan kuvvet serileri ile temsil edilebilir. Doğal logaritma ya da karekök fonksiyonu tam bir fonksiyona uzatılamaz.

Matematiğin bir dalı olan karmaşık analizde, Augustin Louis Cauchy'nin ismine atfedilen Cauchy integral teoremi, karmaşık düzlemdeki holomorf fonksiyonların çizgi integralleri hakkında önemli bir teoremdir.
Matematiğin bir dalı olan karmaşık analizde Augustin Louis Cauchy ve Bernhard Riemann'a atfen Cauchy-Riemann denklemleri olarak adlandıran denklemler, türevlenebilir bir fonksiyonun açık bir kümede holomorf fonksiyon olması için gerekli ve yeterli şartları sağlayan kısmi diferansiyel denklemlerdir. Bu denklemler sistemi ilk defa Jean le Rond d'Alembert'in 1752 yılındaki çalışmasında ortaya çıkmıştır. Daha sonra, 1777 yılındaki çalışmasıyla Leonhard Euler bu sistemi analitik fonksiyonlarla ilişkilendirmiştir. Cauchy ise bu sistemi 1814'teki çalışmasındaki fonksiyonlar teorisinde kullanmıştır. Riemann'ın fonksiyonlar teorisi üzerine olan doktora tezinin tarihi ise 1851'dir.

Matematikte karmaşık düzlem, gerçel eksen ve ona dik olan sanal eksen tarafından oluşturulmuş, karmaşık sayıların geometrik bir gösterimidir. Karmaşık sayının gerçel kısmının x-ekseni boyuncaki yer değiştirmeyle, sanal kısmının ise y-eksenindeki yer değiştirmeyle temsil edildiği değiştirilmiş bir Kartezyen düzlem olarak düşünülebilir.
Karmaşık analizde Charles Émile Picard'ın ismine atfedilen Picard teoremi analitik bir fonksiyonun görüntü kümesiyle ilişkin ayrı ayrı ama yine de birbirine bağlı iki teoremdir.
Karmaşık analizde, bir kaldırılabilir tekillik veya daha düzgün bir söylemle, bir holomorf fonksiyonun kaldırılabilir tekilliği, fonksiyonun görünüşte holomorf olmadığı; ancak daha yakın bir incelemeden sonra fonksiyonun tanım kümesinin bu tekilliği de içerecek şekilde genişletilebileceği bir noktadır.
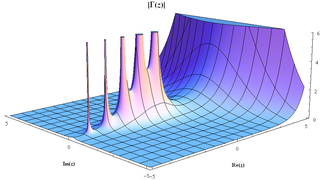
Meromorf fonksiyon, özellikle karmaşık analizde, bir fonksiyon çeşidi. Daha açık bir ifadeyle, meromorf fonksiyon, karmaşık düzlemin açık bir D kümesi üzerinde fonksiyonun kutup noktalarından oluşan belli bir korunmalı noktalar kümesi haricinde D 'nin geriye kalan diğer noktalarının tümünde holomorf olan fonksiyondur. Meromorf kelimesi Yunanca "kısım", "parça" anlamına gelen “meros” ve "tüm", "bütün" anlamına gelen “holos” kelimelerinin tezat bir birleşiminden ortaya çıkmış bir kelimedir.

Matematikte gerçel, karmaşık veya daha genel bir anlamda vektör değerli bir fonksiyonun kökü, fonksiyonun tanım kümesinde bulunan ve fonksiyonun 0 değerini aldığı noktalardır. Yani, eğer bir V kümesinden bir W vektör uzayına tanımlı bir fonksiyonu

Bu diferansiyel geometri konuların bir listesidir. Ve aynı zamanda Lie grubu konularının listesi metrik geometri ve diferansiyelin sözlüğü bkz.
Matematikte açık birim disk, P noktasına uzaklığı 1'den küçük noktalar kümesidir.

Geometride, menteşe teoremi, bir üçgenin iki kenarı başka bir üçgenin iki kenarına uyuyorsa ve birincinin iç açısının ikincinin iç açısından daha büyük olduğunda, ilk üçgenin üçüncü kenarının ikinci üçgenin üçüncü kenarından daha uzun olduğunu belirtir. Bu teorem aslında Öklid'in Elemanları Kitabının 24. önermesidir. Teorem şunları belirtir:

Matematikte Riemann küresi, genişletilmiş karmaşık düzlemin artı sonsuzdaki noktanın bir modelidir. Carl Friedrich Gauss tarafından daha önceden düşünülmüş olsa da, öğrencisi Bernhard Riemann'ın adıyla anılmaktadır. Genişletilmiş bu düzlem, genişletilmiş karmaşık sayıları—yani artı sonsuzdaki ∞ değerli karmaşık sayıları—temsil eder. Riemann modelinde, "0" noktası çok küçük sayılara yakın olur ise "∞" noktası çok daha büyük sayılara yakınlaşır.

Matematikte Riemann yüzeyi, özellikle karmaşık analizde bahsi geçen tek boyutlu karmaşık bir manifolddur. Bu yüzey(ler) ilk olarak Bernhard Riemann tarafından incelenmiş ve isimlendirilmiş. Riemann yüzeyleri, karmaşık düzlemin deforme olmuş versiyonları olarak düşünülebilir: her noktanın yakınında karmaşık düzlemin yerel olarak yamaları gibi görünürler, ama topolojisi oldukça farklı olabilmektedir.

Geometri, şekil, boyut, şekillerin göreceli konumu ve uzayın özellikleri ile ilgili sorularla ilgilenen bir matematik dalıdır. Geometri, en eski matematiksel bilimlerden biridir.
Matematiğin bir dalı olan çok değişkenli karmaşık analizde Poincaré teoremi,  için,
için,  deki birim polidisk ile birim yuvarın arasında biholomorf gönderim olamayacağını söyleyen önemli bir teoremdir.
deki birim polidisk ile birim yuvarın arasında biholomorf gönderim olamayacağını söyleyen önemli bir teoremdir.












