Reuleaux üçgeni

Bir Reuleaux üçgeni (Fransızca telaffuz: [ʁœlo]), merkezi diğer ikisinin sınırında bulunan üç çembersel diskin kesişmesinden oluşan bir şekildir. Sınırı, dairenin kendisinden başka en basit ve en iyi bilinen bu eğri, bir sabit genişlikli eğridir.^[1] Sabit genişlik, her iki paralel destek doğrusunun aralığının yönlerinden bağımsız olarak aynı olduğu anlamına gelir. Tüm çapları aynı olduğu için Reuleaux üçgeni, "Daire dışında, delikten düşmemesi için bir rögar kapağı hangi şekillerde yapılabilir?" sorusunun cevabıdır.^[2]

Reuleaux üçgenlerine küresel üçgenler de denir, ancak bu terim daha doğru bir şekilde bir kürenin eğimli yüzeyine çizilen üçgenleri ifade eder. Adlarını, bir hareket türünü diğerine çevirmek için makinelerin incelenmesine öncülük eden ve tasarımlarında Reuleaux üçgenleri kullanan 19. yüzyıl Alman mühendisi^[3] Franz Reuleaux'dan almıştır.^[4] Bununla birlikte, bu şekiller onun zamanından önce, örneğin Gotik kilise pencerelerinin tasarımcıları, onu bir harita projeksiyonu için kullanan Leonardo da Vinci ve sabit genişlikteki şekiller üzerine yaptığı çalışmada Leonhard Euler tarafından biliniyordu. Reuleaux üçgeninin diğer uygulamaları arasında; gitar penaları, yangın musluğu somunları, kurşun kalemler ve kare delikler açmak için matkap uçlarına şekil vermenin yanı sıra bazı işaretler ve kurumsal logoların şekillerinde grafik tasarımda kullanımı da yer alır.

Belirli bir genişliğe sahip sabit genişlikte şekiller arasında, Reuleaux üçgeni köşelerinde minimum alana ve mümkün olan en keskin (en küçük) açıya (120°) sahiptir. Birkaç sayısal ölçü ile merkezi simetrik olmaktan en uzak olanıdır. Bir tam sayı kafesinin noktalarından kaçınarak en büyük sabit genişlikte şekli sağlar ve çevre-çap oranını maksimize eden dörtgen şekliyle yakından ilgilidir. Her zaman karenin dört kenarına dokunarak bir kare içinde tam bir dönüş yapabilir ve bu özelliği ile mümkün olan en küçük şekil alanına sahiptir. Ancak, bu döndürme sürecinde karenin çoğunu kaplasa da, karenin köşelerine yakın alanının küçük bir bölümünü kaplayamamaktadır. Bir kare içinde dönme özelliğinden dolayı, Reuleaux üçgeni bazen Reuleaux rotoru olarak da bilinir.^[5]

Reuleaux üçgeni, sınırları tek sayıda kenarlı düzgün çokgenlerden oluşan sabit genişlikte eğriler olan Reuleaux çokgenlerinin bir dizisinin ilk elemanıdır. Bu eğrilerin bir kısmı madeni para şekli olarak kullanılmıştır. Reuleaux üçgeni, birden çok şekilde üç boyuta da genelleştirilebilir: Reuleaux dört yüzlüsü (merkezleri normal bir dört yüzlü (tetrahedron) üzerinde uzanan dört topun kesişimi) sabit genişliğe sahip değildir, ancak sabit genişliğe sahip Meissner dört yüzlüsü oluşturmak için kenarları yuvarlatılarak değiştirilebilir. Alternatif olarak, Reuleaux üçgeninin dönel yüzeyi de sabit genişliğe sahiptir.

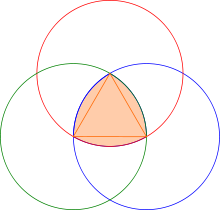
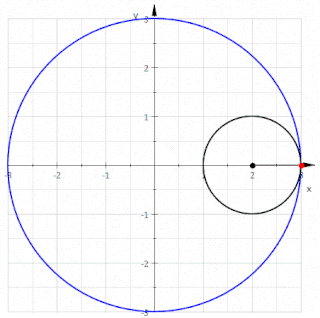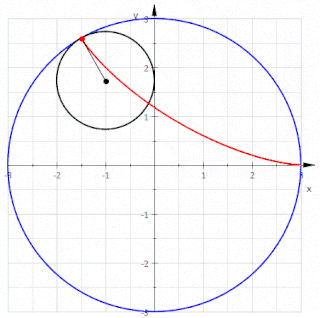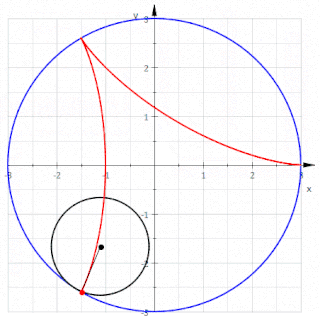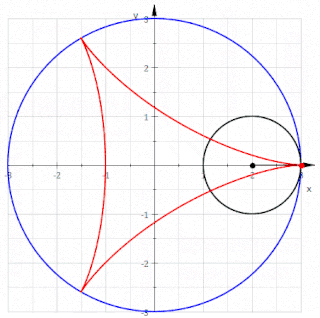
Reuleaux üçgeni doğrudan üç çemberin kesiştirilmesiyle veya bir eşkenar üçgenin kenarlarını yuvarlayarak oluşturulabilir.^[6]

Üç çemberli inşa, bir cetvele bile ihtiyaç duymadan, yalnızca bir pergel ile gerçekleştirilebilir. Mohr-Mascheroni teoremine göre, aynı şey daha genel olarak herhangi bir pergel ve düz kenarlı cetvel çizimleri için doğrudur^[7] ancak Reuleaux üçgeninin oluşturulması özellikle basittir. İlk adım, düzlemin (sonunda üçgenin köşeleri haline gelecek olan) rastgele iki noktasını işaretlemek ve pusulayı, işaretli noktalardan birinde ortalanmış bir çember çizmek için diğer işaretli noktadan geçmektir. Daha sonra, işaretli diğer noktada ortalanmış ve ilk işaretli noktadan geçen, aynı yarıçapta ikinci bir çember çizilir. Son olarak, yine aynı yarıçapta, merkezi önceki iki çemberin iki kesişme noktasından birinde işaretlenmiş her iki noktadan geçen üçüncü bir çember çizilir.^[8] Ortaya çıkan üç çemberin düzenlenmiş merkez bölgesi bir Reuleaux üçgeni olacaktır.^[6]

Alternatif olarak, bir Reuleaux üçgeni eşkenar üçgen T’den, her biri T’nin bir köşesinde ortalanmış ve diğer iki köşeyi birleştiren üç çember yayı çizilerek oluşturulabilir.^[9] Veya eşdeğer olarak, yarıçapı T’nin kenar uzunluğuna eşit olan, T’nin köşelerinde ortalanmış üç diskin kesişimi olarak da inşa edilebilir.^[10]

Reuleaux üçgeninin en temel özelliği, sabit genişliğe sahip olmasıdır, yani her bir paralel destek doğrusu çifti için (her ikisi de şekle, içinden geçmeden şekle dokunan aynı eğimdeki iki doğru), iki doğrunun bu doğruların yönüne bakılmaksızın birbirlerinden aynı Öklid uzaklığına sahiptir.^[9] Herhangi bir paralel destek doğrusu çiftinde, iki doğrudan biri zorunlu olarak üçgene köşelerinden birinde dokunacaktır. Diğer destek doğrusu, üçgene karşı yay üzerindeki herhangi bir noktada dokunabilir (teğet olabilir) ve mesafeleri (Reuleaux üçgeninin genişliği) bu yayın yarıçapına eşittir.^[11]

Sabit genişlikte eğrilerin varlığını keşfeden ve Reuleaux üçgeninin sabit genişliğe sahip olduğunu gözlemleyen ilk matematikçi Leonhard Euler olabilir.^[5] Euler, 1771'de sunduğu ve 1781'de yayınlanan De curvis triangularibus adlı bir makalede, eğrisel üçgenlerin yanı sıra orbiform olarak adlandırdığı sabit genişlikte eğrileri de inceledi.^[12][13]

Reuleaux üçgeni, birçok farklı ölçüte göre, sabit genişliğin en uç eğrilerinden biridir.

Blaschke–Lebesgue teoremine göre, Reuleaux üçgeni verilen sabit genişlikte herhangi bir eğrinin mümkün olan en küçük alanına sahiptir. Bu alan aşağıdaki şekilde hesaplanır:

${\displaystyle {\frac {1}{2}}(\pi -{\sqrt {3}})s^{2}\approx 0.70477s^{2},}$

burada s sabit genişliktir. Bu alan formülünü türetmenin bir yöntemi, Reuleaux üçgenini bir iç eşkenar üçgene ve bu iç üçgen ile Reuleaux üçgenini oluşturan yaylar arasında üç eğrisel bölgeye bölmek ve ardından bu dört kümenin alanlarını eklemektir. Diğer uçta, mümkün olan maksimum alana sahip sabit genişliğin eğrisi, ${\displaystyle \pi s^{2}/4\approx 0.78540s^{2}}$ alana sahip olan bir dairesel disktir.^[14]

Bir Reuleaux üçgeninin köşelerinde her yay çifti tarafından oluşturulan açıların tümü 120°'ye eşittir. Bu, sabit genişliğe sahip herhangi bir eğrinin herhangi bir tepe noktasındaki olası en keskin açıdır.^[9] Ek olarak, sabit genişliğe sahip eğriler arasında, Reuleaux üçgeni hem en büyük hem de en küçük kirişler eşkenar üçgenlerine sahip olandır.^[15] Bir Reuleaux üçgeninde en büyük kirişler eşkenar üçgeni, üç köşesini birleştiren ve en küçük olanı, kenarlarının üç orta noktasını birbirine bağlayandır. Üç veya daha fazla çapa ait noktalardan oluşan Reuleaux üçgeninin alt kümesi, bu iki üçgenden daha büyük olanının iç kısmıdır; sabit genişlikteki diğer herhangi bir eğrinin üç çaplı noktalarından daha büyük bir alana sahiptir.^[16]

Reuleaux üçgeni, bir eşkenar üçgenle aynı olan altı katlı iki düzlemli (dihedral) simetriye sahip olmasına rağmen, merkezi simetriye sahip değildir. Reuleaux üçgeni, iki farklı merkezi asimetri ölçüsüne göre sabit genişliğin en az simetrik eğrisidir; Kovner-Besicovitch ölçüsü (alanın, eğri tarafından çevrelenen en büyük merkezi simetrik şekle oranı) ve Estermann ölçüsü (alanın, eğriyi çevreleyen en küçük merkezi simetrik şekle oranı). Reuleaux üçgeni için, asimetri ölçülerini belirleyen iki merkezi simetrik şeklin ikisi de altıgendir, ancak içteki kıvrımlı kenarlara sahiptir.^[17] Reuleaux üçgeni, alanını sabit genişliğe sahip diğer herhangi bir eğriden daha eşit olmayan şekilde bölen çaplara sahiptir. Yani, başka bir asimetri ölçüsü olan bir çapın her iki tarafındaki maksimum alanlara oranı, Reuleaux üçgeni için sabit genişliğe sahip diğer eğrilere göre daha büyüktür.^[18]

Bir tam sayı kafesinin tüm noktalarından kaçınan sabit genişlikteki tüm şekiller arasında, en büyük genişliğe sahip olan bir Reuleaux üçgenidir. Yarım tam sayı doğrusu üzerinde koordinat eksenlerine paralel simetri eksenlerinden birine sahiptir. Yaklaşık 1.545 olan genişliği, tam sayı katsayıları olan bir 6. derece polinomun köküdür.^[17][19][20]

Bir çemberin kendisine dokunan altı eş çember ile çevrelenmesi mümkün olduğu gibi, aynı boyuttaki merkezi bir Reuleaux üçgeni ile temas edecek şekilde yedi uyumlu Reuleaux üçgeni inşa etmek de mümkündür. Bu, sabit genişliğe sahip herhangi bir eğri için mümkün olan maksimum sayıdır.^[21]

Tüm dörtgenler arasında, en büyük çevre çap oranına sahip olan şekil bir eş köşegenel uçurtmadır ve bir Reuleaux üçgeni içine çizilebilir.^[22]

Barbier teoremine göre, Reuleaux üçgeni dahil aynı sabit genişliğe sahip tüm eğriler eşit çevre uzunluğuna sahiptir. Özellikle bu çevre, aynı genişliğe sahip dairenin çevresine eşit olup ${\displaystyle \pi s}$ ile hesaplanır.^[23][24][9]

Genişliği s olan bir Reuleaux üçgenin en büyük iç teğet çemberinin ve aynı üçgenin çevrel çemberinin yarıçapları sırasıyla;

${\displaystyle \displaystyle \left(1-{\frac {1}{\sqrt {3}}}\right)s\approx 0.42265s\quad {\text{and}}\quad \displaystyle {\frac {s}{\sqrt {3}}}\approx 0.57735s}$

Bu yarıçapların toplamı Reuleaux üçgeninin genişliğine eşittir. Daha genel olarak, sabit genişliğe sahip her eğri için, en büyük iç teğet çember ve en küçük çevrel çember eş merkezlidir ve yarıçaplarının toplamı eğrinin sabit genişliğine eşittir.^[25]

Reuleaux üçgeninin düzlemdeki en ideal sıkıştırma yoğunluğu kanıtlanmamıştır, ancak aşağıdaki gibi olduğu tahmin edilmektedir:

${\displaystyle {\frac {2(\pi -{\sqrt {3}})}{{\sqrt {15}}+{\sqrt {7}}-{\sqrt {12}}}}\approx 0.922888,}$

bu da, şekiller için olası bir çift kafes sıkıştırmanın yoğunluğudur. Sıkıştırma yoğunluğunun kanıtlanmış en iyi üst sınırı yaklaşık 0,947275'tir.^[26] Reuleaux üçgenlerinin sabit genişliğe sahip herhangi bir eğri içinde en yüksek sıkıştırma yoğunluğuna sahip olduğu varsayılmış ancak kanıtlanmamıştır.^[27]

Sabit genişlikte herhangi bir eğri, kare içinde bir rotor oluşturabilir; kare içinde kalırken ve her zaman karenin dört kenarına dokunarak tam bir dönüş gerçekleştirebilen bir şekildir. Bununla birlikte, Reuleaux üçgeni, mümkün olan minimum alana sahip rotordur.^[9] Dönerken ekseni tek bir noktada sabit kalmaz, bunun yerine dört elips parçasının oluşturduğu bir eğri izler.^[28] 120° açıları nedeniyle dönen Reuleaux üçgeni, karenin köşelerinde daha keskin açıların yakınında bazı noktalara ulaşamaz, bunun yerine yine eliptik yaylardan oluşan hafif yuvarlatılmış köşeli bir şekli kaplar.

Dört elipsten biri ve takip eden bir kare içinde dönen Reuleaux üçgeninin merkezi

Bir karenin köşelerinden birini (sol altta) dönen bir Reuleaux üçgeni tarafından süpürülen bölgeden ayıran elips

Bu dönüş sırasında herhangi bir noktada, Reuleaux üçgeninin iki köşesi karenin iki bitişik kenarına temas ederken, üçgenin üçüncü köşesi karenin zıt tepe noktasına yakın bir eğri çizer. Dönen Reuleaux üçgeninin izlediği şekil, karenin yaklaşık% 98,77'sini kaplar.^[29]

Reuleaux'nun Reuleaux üçgenini incelemeye yönelik orijinal motivasyonu, bir karşı örnek olarak, üç tek noktalı bağlantının düzlemsel bir nesneyi tek bir konuma sabitlemek için yeterli olmayabileceğini gösteriyordu.^[30] Reuleaux üçgenlerinin ve sabit genişliğe sahip diğer eğrilerin varlığı, çap ölçümlerinin tek başına bir nesnenin çembersel bir kesite sahip olduğunu doğrulayamayacağını göstermektedir.^[31]

Kirişler karesi problemi ile bağlantılı olarak Eggleston (1958), Reuleaux üçgeninin, düzgün altıgen dışında, dört kenardan daha fazla düzgün çokgenin kirişler çokgeni olamayacağı sabit genişlikte bir şekil örneği sağladığını gözlemledi ve bu şekle, sabit genişliğini koruyan ancak aynı zamanda düzgün altıgenlerin kirişler çokgeni olmasını engelleyen küçük bir değişiklik yaptı. Kesiti ile aynı şekle sahip bir silindiri kullanarak bu sonucu üç boyuta genelleştirdi.^[32]

Bir kare içinde dönebilme özelliğine bağlı olarak, çeşitli makine türleri Reuleaux üçgeni şeklini alır.

Watts Brothers Tool Works kare matkap ucu, kesme yüzeylerini oluşturmak için içbükeyliklerle değişikliğe uğramış bir Reuleaux üçgeni şekline sahiptir. Ucun sabit bir dönme merkezine sahip olmamasına izin veren özel bir aynaya monte edildiğinde, neredeyse kareye yakın bir delik açabilir.^[33] 1914'te Henry Watts tarafından patenti alınmış olmasına rağmen, başkaları tarafından icat edilen benzer matkaplar daha önce kullanıldı.^[9] Diğer Reuleaux çokgenleri beşgen, altıgen ve sekizgen delikler açmak için kullanılır.^[9][33]

Panasonic'in RULO robot elektrik süpürgesi, odaların köşelerindeki tozu temizlemeyi kolaylaştırmak için Reuleaux üçgenine dayanan bir şekle sahiptir.^[34][35]

Reuleaux üçgeninin başka bir uygulama sınıfı, Reuleaux üçgen kesitine sahip silindirik nesneleri içerir. Daha geleneksel yuvarlak veya altıgen variller yerine bu şekilde birkaç kurşun kalem üretilmiştir.^[36] Genellikle daha rahat oldukları veya doğru tutuşu teşvik ettikleri ve masalardan yuvarlanma olasılıkları daha düşük olduğu (ağırlık merkezi dönen bir altıgenden daha fazla yukarı ve aşağı hareket ettiği için) şeklinde tanıtılırlar.

Bir Reuleaux üçgeni (diğer tüm sabit genişlikli eğrilerle birlikte) yuvarlanabilir, ancak sabit bir dönme merkezi etrafında dönmediği için zayıf bir tekerlek oluşturur. Reuleaux üçgen kesitine sahip silindirlerin üstündeki bir nesne düzgün ve düz bir şekilde yuvarlanır, ancak Reuleaux üçgen tekerleklerine takılan bir aks, devir başına üç kez yukarı ve aşağı seker.^[9][37] Bu kavram, Poul Anderson tarafından "Üç Köşeli Tekerlek (The Three-Cornered Wheel)" adlı kısa bir bilimkurgu öyküsünde kullanıldı.^[11][38] Yüzer akslara sahip bir bisiklet ve Reuleaux üçgeni şeklindeki tekerleğinin kenarıyla desteklenen bir çerçeve, 2009 yılında aynı şekle sahip kalemlerden ilham alan Çinli mucit Guan Baihua tarafından yapıldı ve gösterildi.^[39]

Reuleaux üçgeninin başka bir uygulama sınıfı, onun sabit bir eksen etrafında dönüşünü ileri geri harekete (öteleme hareketine) dönüştürebilen mekanik bağlantının bir parçası olarak kullanmayı içerir.^[10] Bu mekanizmalar Franz Reuleaux tarafından incelenmiştir. Gustav Voigt şirketinin yardımıyla Reuleaux, birçoğu Reuleaux üçgenini içeren yaklaşık 800 model mekanizma inşa etti.^[40] Reuleaux bu modelleri, hareketlerinin öncü bilimsel araştırmalarında kullandı.^[41] Reuleaux–Voigt modellerinin çoğu kaybolmuş olsa da, 9'u Reuleaux üçgenine dayalı olmak üzere 219'u Cornell Üniversitesi'nde toplandı.^[40][42] Bununla birlikte, mekanizma tasarımında Reuleaux üçgenlerinin kullanılması Reuleaux'nun çalışmasından önce gelir; Örneğin, bazı buhar motorları kam bir Reuleaux üçgeni şeklinde 1830 gibi erken bir zamanda vardı.^[43][44]

Bu ilkenin bir uygulaması, bir film projektöründe ortaya çıkar. Bu uygulamada, filmi sarsıntılı, kademeli bir hareketle ilerletmek gerekir, burada her film karesi projektör merceğinin önünde saniyenin bir kısmı için durur ve ardından çok daha hızlı bir şekilde bir sonraki çerçeveye geçer. Bu, bir Reuleaux üçgeninin bir kare içindeki dönüşünün, filmi hızla her yeni kareye çeken ve ardından çerçeve yansıtılırken filmin hareketini duraklatan bir aktüatör için bir hareket modeli oluşturmak amacıyla kullanıldığı bir mekanizma ile yapılabilir.^[45]

Wankel motorunun rotoru, genellikle bir Reuleaux üçgeni örneği olarak gösterilen eğrisel bir üçgen şeklindedir.^{[3][5][9][44]} Bununla birlikte, kıvrımlı kenarları bir Reuleaux üçgeninden biraz daha düzdür ve bu nedenle sabit genişliğe sahip değildir.^[46]

Gotik mimaride, 13. yüzyılın sonlarından veya 14. yüzyılın başlarından^[47] başlayarak, Reuleaux üçgeni pencereler, pencere oyma ve diğer mimari süslemelerde sıklıkla kullanılan eğrisel biçimlerden biri haline geldi.^[3] Örneğin, İngiliz Gotik mimarisinde bu şekil, hem 1250–1290 geometrik üslubu hem de 1290–1350 eğrisel üslupla devam eden süslü dönemle ilişkilendirilmiştir. Milano Katedrali'nin bazı pencerelerinde de görülür.^[48] Bu bağlamda, şekil daha çok küresel üçgendir,^[49][50] ancak küresel üçgenin daha genel matematiksel anlamı bir kürenin yüzeyindeki bir üçgendir (aynı zamanda mimaride yaygın olarak kullanılan pandantif bir şekil). Gotik kilise mimarisinde kullanımda, Reuleaux üçgenin üç köşeli şekli, hem teslisin bir sembolü,^[51] ve hem de "çember şeklinde karşı bir hareket" olarak görülebilir.^[52]

Reuleaux üçgeni diğer mimari tarzlarda da kullanılmıştır. Örneğin Leonardo da Vinci, bu şekli bir sur planı olarak çizmiştir.^[42] Reuleaux üçgeni şeklindeki bir kat planı kullandığı iddia edilen modern binalar arasında MIT Kresge Oditoryumu, Kölntriangle, Donauturm, Torre de Collserola ve Mercedes-Benz Müzesi bulunmaktadır.^[53] Ancak çoğu durumda bunlar, Reuleaux üçgeninden farklı geometriye sahip, yalnızca yuvarlak üçgenlerdir.

Reuleaux üçgeninin bir başka erken uygulaması, yaklaşık 1514 tarihli olan da Vinci'nin dünya haritasıdır, dünyanın küresel yüzeyinin her biri bir Reuleaux üçgeni şeklinde düzleştirilmiş sekiz oktana bölündüğü bir dünya haritasıydı.^[54][55][56]

Reuleaux üçgenine dayanan benzer haritalar 1551'de Oronce Finé ve 1580'de John Dee tarafından yayınlanmıştır.^[56]

Birçok gitar penası Reuleaux üçgenini kullanır, çünkü şekli güçlü bir artikülasyon sağlamak ve sıcak bir tını üretmek için, keskin bir nokta ile geniş bir ucu birleştirir. Şeklin üç noktası da kullanılabilir olduğundan, tek uçlu bir mızraba göre yönlendirilmesi daha kolaydır, daha az ve yavaş aşınır.^[57]

Bir yangın musluğunun yasadışı kullanımı, Philadelphia, 1996 ve böyle bir kullanımı önlemek için Reuleaux üçgen şekilli somunu olan daha yeni bir Philadelphia yangın musluğu.

Reuleaux üçgeni, bir yangın musluğu vanası somununun enine kesiti için şekil olarak kullanılmıştır. Bu şeklin sabit genişliği, standart paralel çeneli anahtarlar kullanılarak yangın musluğunun açılmasını zorlaştırır; bunun yerine özel şekilli bir anahtar gereklidir. Bu özellik, yangın musluklarının (özel anahtarı olan) itfaiyeciler tarafından açılmasına izin verir, ancak musluğu diğer faaliyetler için su kaynağı olarak kullanmaya çalışan diğer kişiler tarafından açılamaz.^[58]

Keto (1997) bir önerisini takiben,^[59] Hawaii'deki Mauna Kea'da bir radyo dalgası astronomik gözlemevi olan Submilimeter Dizisinin antenleri, iç içe geçmiş dört Reuleaux üçgeni üzerinde düzenlenmiştir.^[60][61] Anteni sabit genişlikte bir eğri üzerine yerleştirmek, gözlemevinin tüm yönlerde aynı uzaysal çözünürlüğe sahip olmasına neden olur ve dairesel bir gözlem ışını sağlar. Sabit genişliğe sahip en asimetrik eğri olan Reuleaux üçgeni, diziden gelen sinyalin Fourier dönüşümü için düzlemin en düzgün kapsamına götürür. Antenler, her bir gözlemin istenen açısal çözünürlüğüne göre farklı gözlemler için bir Reuleaux üçgeninden diğerine hareket ettirilebilir. Antenlerin bu Reuleaux üçgenleri üzerindeki hassas yerleşimi bir sinir ağı kullanılarak en ideal hale getirildi. Bazı yerlerde, inşa edilen gözlemevi, tercih edilen Reuleaux üçgen şeklinden ayrılıyor çünkü bu şekil verilen alan içinde mümkün değildi.

Birçok işaret ve kurumsal logo için kullanılan kalkan şekillerinde yuvarlak üçgenler bulunur. Ancak, bunlardan sadece bazıları Reuleaux üçgenleridir.

Avrupa, Kuzey Amerika ve Afrika'da büyük operasyonları yapan Belçikalı bir petrol şirketi olan Petrofina'nın (Fina) kurumsal logosu, 1950'den Petrofina'nın 2000'de Total SA ile birleşmesine kadar Fina adıyla bir Reuleaux üçgeni kullandı.^[62][63] Bavyera Brewery'nin güneyi gösteren pusulası olan Reuleaux üçgeninde çerçevelenen bir diğer kurumsal logo, SAN 2010 Yılın Reklamvereni ödülünü kazanan tasarım şirketi Total Identity tarafından yapılan bir makyajın parçasıydı.^[64] Reuleaux üçgeni, Colorado Maden Okulu'nun logosunda da kullanılmıştır.^[65]

Amerika Birleşik Devletleri'nde, Ulusal Yollar Sistemi (National Trails System) ve Amerika Birleşik Devletleri Bisiklet Güzergâh Sistemi (United States Bicycle Route System) yolları tabelada Reuleaux üçgenleriyle işaretler.^[66]

Plateau yasalarına göre, iki boyutlu sabun köpüğü kümelerindeki dairesel yaylar, bir Reuleaux üçgeninin köşelerinde bulunan aynı açı ile 120°'lik açılarda buluşur. Bu gerçeğe dayanarak, baloncukların bir kısmının bir Reuleaux üçgeni şeklini aldığı kümeler oluşturmak mümkündür.^[67]

Şekil ilk olarak 2014 yılında Reuleaux üçgen diskleri olarak kristal formda izole edildi.^[68] Reuleaux üçgen şeklindeki temel bizmut nitrat diskleri, 2,3-bis (2-piridil) pirazin varlığında bir etanol-su sisteminde bizmut nitratın hidrolizi ve çökelmesinden oluşturulmuştur.

Reuleaux üçgeninden sabit bir mesafede noktaların konumu olarak, keskin köşelerden daha düzgün, sabit genişlikte üçgen eğriler elde edilebilir.^[69] Reuleaux üçgeninin diğer genellemeleri arasında üç boyutlu yüzeyler, üçten fazla kenarı olan sabit genişliğe sahip eğriler ve genişlik, çap ve yarıçap arasındaki eşitsizliğin en uç örneklerini sunan Yanmouti kümeleri bulunur.

Yan uzunluğu s olan düzgün bir dört yüzlünün köşelerinde ortalanmış s yarıçaplı dört topun kesişme noktasına Reuleaux dört yüzlüsü denir, ancak yüzeyi, bir sabit genişlikli yüzey değildir.^[70] Bununla birlikte, kenar yaylarının üçünü dairesel bir yayın dönüş yüzeyleri olan kavisli yüzeylerle değiştirerek Meissner dört yüzlüsü denilen sabit genişlikte bir yüzey haline getirilebilir. Alternatif olarak, bir Reuleaux üçgeninin simetri eksenlerinden biri boyunca dönel yüzeyi, verilen sabit genişliğe sahip bilinen tüm dönel yüzeyler arasında minimum hacimle sabit genişlikte bir yüzey oluşturur.^[71]

Reuleaux poligonları

Reuleaux üçgeni, sabit yarıçaplı dairesel yaylardan oluşan sabit genişlikte bir eğri olan bir Reuleaux çokgeni oluşturan tek sayıda kenara sahip düzgün veya düzgün olmayan çokgenlere genelleştirilebilir. Bu şekillerin sabit genişliği, bozuk parayla çalışan makinelerde kullanılabilecek madeni para olarak kullanılmalarına izin verir.^[9] Genel dolaşımda bu tür madeni paraların genellikle üçten fazla kenarı olmasına rağmen, bir Reuleaux üçgeni Bermuda'da bir hatıra parası için kullanılmıştır.^[53]

Benzer yöntemler, genişliği belirli bir çokgenin çapına eşit olan sabit genişlikte bir eğri içine rastgele bir basit çokgeni dahil etmek için kullanılabilir. Elde edilen şekil dairesel yaylardan oluşur (en fazla çokgenin kenarları kadar), doğrusal zamanda algoritmik olarak oluşturulabilir, pergel ve cetvel ile çizilebilir.^[72] Reuleaux çokgenlerinin hepsinde tek sayıda dairesel yay kenarı olmasına rağmen, değişen yarıçaplara sahip çift sayıda dairesel yay kenarı olan sabit genişlikte şekiller oluşturmak da mümkündür.^[73]

Yanmouti kümeleri, bir eşkenar üçgenin üç dairesel yay ile birlikte dışbükey örtü (zarf) olarak tanımlanır, üçgenin köşelerinde ortalanır ve üçgenin kenar uzunluğuna en fazla eşit olan eş yarıçaplarla üçgenle aynı açıyı kapsar. Böylece, yarıçap yeterince küçük olduğunda, bu kümeler, eşkenar üçgenin kendisine dejenere olur, ancak yarıçap mümkün olduğunca büyük olduğunda karşılık gelen Reuleaux üçgenine eşittirler. Genişliği w, çapı d ve yarıçapı r (şeklin içerdiği olası en büyük dairenin yarıçapı) olan her şekil aşağıdaki eşitsizliği sağlar:

${\displaystyle w-r\leq {\frac {d}{\sqrt {3}}},}$

ve bu eşitsizlik, artık iyileştirilemeyeceğini gösteren Yanmouti kümeleri için bir eşitlik haline gelir.^[74]

Üç kümeli bir Venn diyagramının üst üste binen üç çember olarak klasik sunumunda, merkezi bölge (üç kümenin tümüne ait öğeleri temsil eder) bir Reuleaux üçgeni şeklini alır.^[3] Aynı üç çember, Borromean halkalarının standart çizimlerinden birini, ancak geometrik çemberler olarak gerçekleştirilemeyen karşılıklı bağlantılı üç halkayı oluşturur.^[75] Aynı çemberlerin bu parçaları, ortasında yine bir Reuleaux üçgeni bulunan, üst üste binen üç yarım daire şeklindeki (her ikisi bir vesica piscis sembolü oluşturur) Triquetra'yı oluşturmak için kullanılır;^[76] Venn şemasının üç çemberi Borromean halkalarını oluşturmak için iç içe geçirilebildiği gibi, triquetranın üç dairesel yayı da bir yonca düğümü oluşturmak için iç içe geçirilebilir.^[77]

Reuleaux üçgeninin yakınları, sabit bir alanı çevreleyen ve düzlemde belirtilen üç noktayı içeren minimum çevre şeklini bulma probleminde ortaya çıkar. Alan parametresinin çok çeşitli seçenekleri için, bu probleme en uygun çözüm, üç kenarı eşit yarıçaplı dairesel yaylar olan eğri bir üçgen olacaktır. Özellikle, üç nokta birbirinden eşit uzaklıkta olduğunda ve alan Reuleaux üçgeni olduğunda, Reuleaux üçgeni en uygun kapamadır.^[78]

Dairesel üçgenler, Reuleaux üçgeni ve diğer şekiller de dahil olmak üzere dairesel yay kenarlı üçgenlerdir. Deltoid eğrisi, eğrisel üçgenin başka bir türüdür, ancak eşkenar üçgenin her iki tarafını değiştiren eğrilerin dışbükey değil içbükey olduğu bir eğridir. Dairesel yaylardan oluşmaz, ancak bir çemberin diğerinin üç katı yarıçap içinde yuvarlanmasıyla oluşturulabilir.^[79] Üç eğimli kenarı olan diğer düzlemsel şekiller arasında, eş doğrusal uç noktalara sahip üç yarım daireden oluşan arbelos^[80] ve Bézier üçgeni bulunur.^[81]

Reuleaux üçgeni, 120° açılı bir küresel üçgenin uyumlu görüntüsü olarak da yorumlanabilir.^[67] Bu küresel üçgen, (3/2, 3/2, 3/2 parametreli) Schwarz üçgenlerinden biridir, bir kürenin yüzeyinde yansıma yoluyla kaplayabilen büyük çember yaylarıyla sınırlanmış üçgenlerdir.^[82]

Wikimedia Commons'ta Reuleaux üçgeni ile ilgili ortam dosyaları bulunmaktadır.

• Eric W. Weisstein, Reuleaux Triangle (MathWorld)
• "Reuleaux Triangle". 22 Eylül 2003 tarihinde kaynağından arşivlendi. 
• Paul Bourke (Nisan 2009). "Reuleaux Triangle". 17 Ağustos 2011 tarihinde kaynağından arşivlendi. 
• "Around the Wheel - Reuleaux Triangle". 13 Ocak 2018 tarihinde kaynağından arşivlendi. 
• "Reuleaux Polygons". 12 Ağustos 2018 tarihinde kaynağından arşivlendi. 
• "Reuleaux Triangle". Geogebra. 31 Mart 2021 tarihinde kaynağından arşivlendi. Erişim tarihi: 30 Aralık 2020. 

• "Reuleaux Triangle and the Drilling of Square Holes" (PDF). 13 Temmuz 2019 tarihinde kaynağından (PDF) arşivlendi. 
• Siders, William, & Mark Rue. "Reuleaux triangle somatocharts." Computers in biology and medicine 22.5 (1992): 363-368.
• Smart, James R. "Problem Solving in Geometry—a Sequence of Reuleaux Triangles." The Mathematics Teacher 79.1 (1986): 11-14.
• Ng, Choon Hwee Bernard, & Wai Yip Fan. "Reuleaux triangle disks: new shape on the block." Journal of the American Chemical Society 136.37 (2014): 12840-12843.
• Barrallo, Javier, Francisco González-Quintial, and Santiago Sánchez-Beitia. "An Introduction to the Vesica Piscis, the Reuleaux Triangle and Related Geometric Constructions in Modern Architecture." Nexus Network Journal 17.2 (2015): 671-684.
• Gleiftner, Winfried, & Herbert Zeitler. "The reuleaux triangle and its center of mass." Results in Mathematics 37.3-4 (2000): 335-344.
• Martini, Horst, & Zokhrab Mustafaev. "On Reuleaux triangles in Minkowski planes." Beiträge zur Algebra und Geometrie 48.1 (2007): 225-235.
• Hu, Xiao, Na Li, & BaiYu Liu. "Simulation and Application of Reuleaux Triangle In Geometric Measurement." IOP Conference Series: Earth and Environmental Science. Vol. 310. No. 2. IOP Publishing, 2019.
• Conti, Giuseppe, & Raffaella Paoletti. "Reuleaux Triangle in Architecture and Applications." Faces of Geometry. From Agnesi to Mirzakhani. Springer, Cham, 2020. 79-89.

• Barbier teoremi
• Blaschke–Lebesgue teoremi