Renk yükü

Renk yükü, kuantum renk dinamiği teorisindeki parçacıkların güçlü etkileşimiyle alakalı olan kuark ve gluonların bir özelliğidir.

Kuark ve gluonların renk yükünün tamamı ile renklerin görsel algı ile bir bağlantısı olmadığı dikkate alınmalıdır.^[1] Renk kavramı kolayca yaygınlaşmıştır çünkü yük, insan gözüyle kıyaslanabilen üç ana renk (kırmızı, yeşil ve mavi) arasındaki güçlü etkileşimden sorumludur. Diğer bir renk şeması kırmızı, sarı ve mavi, ışıktan ziyade boyamada kullanılan algılanabilir bir benzeşimdir.

Parçacıklar karşı parçacıklarla uyum sağlamaktadır. Kırmızı, yeşil veya mavi parçacık kendilerine karşılık gelen, renk yükü, parçacık-karşı parçacık korunumu ve yok oluşu için sırasıyla kırmızı, yeşil ve mavinin karşı rengi olması gereken bir karşı parçacığa sahiptir. Parçacık fizikçileri bunlara karşıt kırmızı, karşıt yeşil ve karşıt mavi demektedir. Bu üç rengin hepsi birbiriyle karıştığında veya bunlardan birisiyle karıştığında onların tamamlayıcısı (veya negatifi) renksiz veya beyazdır ve sahip olduğu net renk yükü sıfırdır. Serbest parçacıkların renk yükü sıfırdır: baryonlar üç kuarktan oluşur, ama her bir kuark kırmızı, yeşil ve maviye veya negatiflerine sahip olabilir; mezonlar kuark ve antikuark tarafından yapılmıştır, kuark herhangi bir renk olabilir, antikuark ise bu herhangi bir rengin karşıtı olmak zorundadır. Bu renk yükleri elektromanyetik yüklere, elektromanyetik yükler sadece bir çeşit değere sahip olduğundan beri ters düşmektedir. Pozitif ve negatif elektrik yükleri, işaretleri birbirlerine ters düşmesine rağmen aynı çeşit yüklerdir.

Kısaca kuarkların varlığının ilk olarak 1964'te önerilmesinden sonra, Oscar W. Greenberg renk yükü kavramını, kuarkların nasıl bir arada hadronların içinde bulunduklarını aksi halde eş kuantum konumu için Pauli ilkesini ihlal etmek zorunda kalacaklarını açıklamak için tanıttı. Kuantum kromodinamiği 1970'ten beri geliştirilmektedir ve parçacık fiziğinin standart modelinin önemli bir bileşenini oluşturmaktadır.

KCD'de kuarkların rengi üç değer veya renkten -kırmızı, yeşil ve mavi- birini alabilir. Antikuark üç karşıt renkten – karşıt kırmızı, karşıt yeşil ve karşıt mavi- (temsili olarak sırasıyla çiyan, magenta ve sarı) birini alabilir. Gluonlar iki rengin, kırmızı ve karşıt yeşil gibi, karışımıdır, kendi renklerini oluştururlar. KCD, mümkün olabilecek 9 rengin sekiz gluonunu göz önüne alır - karşıt renkler kombinasyonu özeldir, açıklama için sekiz gluon rengine bakınız.

Aşağıda renk yüklü parçacıklar için bağlantı sabitleri gösterilmektedir:

• 
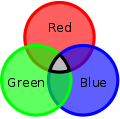  The quark colors (red, green, blue) combine to be colorless
• 
  The quark anticolors (antired, antigreen, antiblue) also combine to be colorless

• 
  A hadron with 3 quarks (red, green, blue) before a color change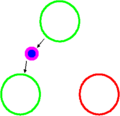
• 
  Blue quark emits a blue-antigreen gluon
• 
  Green quark has absorbed the blue-antigreen gluon and is now blue; color remains conserved
• 
  An animation of the interaction inside a neutron. The gluons are represented as circles with the color charge in the center and the anti-color charge on the outside.

Elektrik alanı için analoğu ve elektrik yükleri, renk yükleri arasındaki etkiyen güçlü kuvvetler alan çizgileri kullanılarak tasvir edilir. Yine de, renk alan çizgileri kadar dışarı doğru kavis yapan başka bir yük yoktur çünkü onların hepsi beraber gluonlar tarafından sıkıca çekilmektedir. (1 fm içinde). Bu etki hadronların içindeki kuarkları sınırlandırır.

Kuantum alan teorisinde bağlantı sabiti ve yük farklıdır ama birbirleriyle ilgili kavramlardır. Bağlantı sabiti kuvvetin etkileşiminin büyüklüğünü belirler; örneğin, kuantum elektrodinamiğinde, ince yapı sabiti bağlantı sabitidir. Ayar teorisindeki bir yük ayar simetrisi altında dönüşen bir parçacık yolu ile yapmak zorundadır, yani onun gösterimi ayar grubu altında yapılır. Örneğin, elektronlar -1 yüklüdür ve pozitronlar +1 yüklüdür, bu ayar dönüşümünün bir anlamda onları ters etkilediğini işaret eder. Özellikle eğer yerel ayar dönüşümü ϕ(x) elektrodinamikte uygulanıyorsa, biri bulunur (tensör indeks gösterimi kullanılarak):

${\displaystyle A_{\mu }}$ foton alanı ve ψ elektrik alan Q = −1 ile (ψ üzerinde bir çubuk onun karşı parçacığını gösterir - pozitron). KCD, değişken-olmayan teoridir ve dolayısıyla renk yükleri daha karmaşıktır. Bir sonraki bölümde ele alınmaktadır.

KCD içindeki köşe grubu değişmeyen SU(3) grubudur. Çalışan kavramı genellikle s gösterilir. Kuark içinde seçilmişlerin her biri temel temsile aittir (3) ve ψ ile göterilen üçlü alanlarını bir arada içerir. Karşıt kuark alanı karmaşık birleşik gösterime (3*) aittir ve ayrıca üçlü alan içerir. Şunu yazabiliriz

Gluon oktet alanlar içermektedir (gluon alana bakınız), eşlenik temsile (8) aittir ve Gell-Mann matrisleriyle yazılabilir.

(burada kastedilen toplamada a = 1,2,..8dir) Diğer tüm parçacıklar rengin üçlü temsiline SU(3) aittir. Bunların her birinin renk yükü temsilleri tarafından tam belirtildi. Kuarklar kırmızı, yeşil ve mavi renk yüküne sahiptir ve Karşıt kuarklar karşıt kırmızı, karşıt yeşil ve karşıt mavi renk yüküne sahiptirler. Gluonlar iki renk yükünün kombinasyonuna (bir kırmızı, yeşil veya mavi ve bir karşıt kırmızı, karşıt yeşil ve karşıt mavi gibi) verilen Gell-Mann matrislerindeki süper pozisyon durumunda sahiptirler. Diğer tüm parçacıklar sıfır renk yüküne sahiptirler. Matematikle ifade edersek, parçacığın renk yükü parçacığın temsili belli bir kuadratik Casimir operatörü değeridir.

Bu basit dil kuark üçlüsündeki genellikle üç renk ile tanımlandı ve bundan önce üç işaretle ‘’1’’,’’2’’ ve ‘’3’' tanıtıldı. Bu renkli dil şu noktayı gözden kaçırmaktadır. Renkteki köşe dönüşümü SU(3), ψ → U ψ şeklinde yazılabilir- U, SU(3) teki grupları içeren 3x3 matrikstir. Böylece, köşe dönüşümünden sonra, yeni renkler, eski renklerin doğrusal kombinasyonları olarak bulunmaktadır. Kısaca, daha önce tanıtılan basitleştirilmiş dil değişmez köşe değildir.

Renk yükü korunur, ama kuantum elektrodinamiğinde yapıldığı gibi bu işin içinde de defter tutma, sadece yükleri toplamaktan daha karmaşıktır. Bunu yapmanın bir kolay yolu KCD etkileşim köşesine bakmak ve bir renk çizgi gösterimi ile değiştirmek. Bunun anlamını şudur. ψi bir kuark alanının birinci bileşenini temsil etsin (zayıf birinci renk olarak adlandırılır). Gluonun rengi Benzer şekilde ilişkili, özellikle Gell-Mann matrisinde karşılık gelen A tarafından verilir. Bu matris i ve j şeklinde iki göstergeye sahiptir. Bunlar gluonun renk etiketidir. Bir qi → ji j + qj'ye sahip köşe etkileşimi. Renk çizgisi bu endeks parçaları temsil eder. Renk yükü korunumunun anlamı bu renk çizgilerinin uçları hem ilk veya son durumunda da olmalıdır, eşdeğer olarak, hem de hiçbir satır diyagramın ortasında kırılmamalıdır.

Gluonlar yenk rükü taşıdığından beri, iki gluon birbirini etkileyebilir. Tipik etkileşim, gluonlar g+g → g katıldığı için köşedir. (üç gluon köşe de denir) Bu gösterilen, renk-çizgi gösterimi ile birliktedir. Renk-çizgi diyagramı renk koruma yasaları açısından yeniden ifade edilebilir; daha önce belirtildiği gibi, ancak, bu bir ayar değişmez bir dil değildir. Tipik bir değişken olmayan ayar teorisinde ayar bozonu teorisinin yük taşır ve bu nedenle bu tür etkileşimleri olur; Örneğin, elektrozayıf teoride W Bozonu. Elektrozayıf Teoride, W, aynı zamanda elektrik yükü taşır ve bu nedenle, bir foton ile etkileşime girer.

• Renk hapsi

• Georgi, Howard (1999). Lie algebras in particle physics (İngilizce). Perseus Books Group. ISBN 0-7382-0233-9. 
• Griffiths, David J. (1987). Introduction to Elementary Particles (İngilizce). New York: John Wiley & Sons. ISBN 0-471-60386-4. 
• Christman, J. Richard (2001). "Colour and Charm" (PDF) (İngilizce). Project PHYSNET. 21 Şubat 2006 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 27 Mayıs 2016. 
• Hawking, Stephen (1998). A Brief History of Time (İngilizce). Bantam Dell Publishing Group. ISBN 978-0-553-10953-5. 
• Close, Frank (2007). The New Cosmic Onion (İngilizce). Taylor & Francis. ISBN 1-58488-798-2.