Polinom
| Fonksiyon |
|---|
| Fonksiyon kavramının tarihi |
| Tanım ve değer kümelerine göre |
| Sınıflarına/özelliklerine göre |
|
| Yapılarına göre |
| Genellemelere göre |
|
| Özel fonksiyonların listesi |

=1/4(x+4)(x+1)(x-2)
Matematikte, bir polinom belirli sayıda bağımsız değişken ve sabit sayıdan oluşan bir ifadedir. Polinom kendi içinde toplama, çıkarma, çarpma ve negatif olmayan sayının üssünü alma işlemlerini kullanır. Örnek olarak tek bilinmeyenli bir polinom olan x2 − 4x + 7, ikinci dereceden oluşan bir polinomdur. Diğer bir örnek olarak, x2 − 4/x + 7x3/2 bir polinom değildir, çünkü polinomlarda terimlerin derecelerinin doğal sayı olma zorunluluğu vardır 2. terimde x′i ele alan bir bölme işlemi x'in derecesini negatif yapmaktadır ve 3. terim doğal sayı olmayan bir derece içermektedir (3/2).
Polinomlar, bilimde ve matematik alanında sıkça görülür. Ekonomiden kimyaya, kimyadan fiziğe ve sosyal bilimlerde problemlerin çözülmesi için kullanılır. Polinomlar, toplama işlemlerinde ve sayısal analizlerde diğer fonksiyonları belirlemek için kullanılır. İleri seviye matematikte, polinomlar, polinom halkaları oluşturmak için kullanılır ve bu halkalar temel matematikte ve cebirsel geometride kullanılan merkezi bir kavramdır.
Bu ismin akılda kalması amacıyla, Türk Dil Kurumu'nun da belirttiği polinom sözlük anlamıyla "çok terimli" anlamına gelmektedir.[1]
Etimoloji
Oxford İngilizce Sözlüğü'ne göre, polinom, binom kelimesindeki bi- kökünün Yunanca "poli" kökü ile değiştirilmesiyle oluşmuş bir kelimedir. Yunanca kelime poli, çok anlamına gelmektedir. polinom kelimesi ilk 17. yüzyılda kullanılmıştır.[2]
Notasyon
Bir polinomda belirsiz X, formüllerde P ya da P(X) olarak belirebilir.
Genelde, polinomun ismi P(X) değil, P′dir. Ancak, eğer a bir sayı, bir değişken, başka bir polinom, veya, daha genel olarak herhangi bir ifadeyi belirtmek için kullanılırsa, P(a) teamül olarak P′deki X′in yerine a′nın geçmesini belirtir. Örnek olarak polinom P, yandaki fonksiyonu tanımlar:
İlişkilendirilen fonksiyonda bilinmeyenler için büyük harf ve değişkenler için küçük harf kullanmak bilinen bir uzlaşımdır.
Özellikle, eğer a = X olursa, P(a)′nın tanımı P = P(X)′i belirtir.
Bu eşitlik bazı durumlarda sözle ifade etmeyi basitleştirir. Örneğin ″P(X) bir polinom olsun″ yerine ″X bilinmeyeni içinde P bir polinom olsun″ kullanılır. Diğer yandan, bilinmeyenin ismini vurgulamak gerekli olmadığı zaman, eğer polinomun her görünüşünde bilinmeyenin ismi gözükmüyorsa çoğu formül daha basit ve okuması daha kolay olur.
Polinomların Aritmetiği
Toplama
Polinomlar toplamanın birleşmeli yasasını kullanarak (bütün terimlerin tek bir toplamda birleştirilmesi), mümkün olduğunca tekrar sıralanıp, benzeri terimler birleştirilebilir.[3][4]
Örneğin:
- olsun
- olsun
- sonrasında
- basitleştirirsek:
Polinomların toplamı polinom verir.[5]
Katsayılar Toplamı: Bir polinomun katsayılar toplamını bulabilmek için o polinomun tüm değişkenlerine 1 vermeliyiz.
Örneğin:
P(3x+2)'in katsayılar toplamı P(5).

Polinomun sadece çift dereceli terimlerinin katsayılar toplamını bulabilmek için değişkenlere 1 ve -1 değerlerini vererek çıkan sonucu toplar ve ikiye böleriz. Sadece tek dereceli terimlerim katsayılar toplamı için ise aradaki toplama işlemini çıkarma işlemine çevirerek sonuca ulaşmak mümkündür.
Çarpım
İki polinomun çarpımlarının terimlerinin toplamını çözmek için, dağılma yasası tekrar edecek şekilde uygulanılır ki bu, bir polinomun her teriminin diğer polinomun her terimiyle çarpılmasıyla sonuçlanır.[3]
Örneğin:
- olsun
- olsun
- sonrasında
- basitleştirirsek:
Polinomların çarpımı polinom verir.[5]
Bölme
Polinom değerlendirmesi birinci dereceden bir polinomun polinom bölümlerindeki kalanı hesaplamak için kullanılabilir, çünkü f(x)′in (x − a)′ya bölümü f(a)′dir; polinom kalan teoremine bakınız. Bu yöntem oran gerekli olmadığı zaman, çoğunlukta kullanılan bölüm algoritmasından daha verimli olur.
Diğer Özellikler
- İki polinomun bileşke fonksiyonu bir polinomdur ki bu ilk polinomdaki değişkenin ikinci polinomdaki bir değişkenle değiştirilmesiyle elde edilir.[5]
- anxn + an−1xn−1 + ... + a2x2 + a1x + a0 polinomunun türevi: nanxn−1 + (n−1)an−1xn−2 + ... + 2a2x + a1′dir. Eğer katsayı dizisi tam sayı içermezse (örneğin katsayılar asal sayı olan p′nin modülosu ise), o zaman kak, k kere ak′nin toplamı olarak yorumlanmalıdır. Örneğin tam sayı üstünde modülo p iken, xp + 1′nin türevi polinom 0′dır.[6]
- Özel olarak; bir polinomun derecesi 3 ise polinoma kübik, derecesi 2 ise kuadratik, derecesi 1 ise doğrusal veya lineer, derecesi 0 ise (P(x)≠0) sabit polinom denir.
- Sıfıra eşit olan bir polinoma sıfır polinomu denir ama sıfır polinomun derecesi 0 değildir. Sıfır polinomunun derecesi tanımlanmamıştır.
Hermit polinomları
Hermit polinomları Pierre-Simon Laplace tarafından 1810'da zor anlaşılır bir biçimde tanımlanmış ve 1859'da Pafnuty Chebyshev tarafından ayrıntılı olarak incelenmiştir. Diğer klasik dik polinomlar gibi, Hermit polinomları birkaç farklı başlangıç noktasından tanımlanabilir.
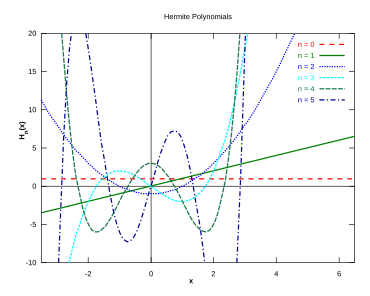
Tanım
Olasılıkçıların kullandığı Hermit polinomu;
Fizikçilerin kullandığı Hermit polinomu;
Olasılıkçıların kullandığı Hermit polinomunun ilk on bir değeri;

Özellikleri
dereceden bir Hermit polinomu dereceleri bir polinomdur. Olasılıkçıların() kullandığı Hermit polinomunun ilk terimindeki katsayısı 1'dir.Fiziklerin kullandığı Hermit polinomunun katsayısı
Diklik
ve dereceden polinomları için Bu polinomlar ağırlık işlevine(fonksiyon) göre dikliktir.
için)
ya da
( için)
Ayrıca bakınız
Kaynakça
- ^ "Türk Dil Kurulumu, Güncel Türkçe Sözlük". 8 Aralık 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 17 Aralık 2013.
- ^ "polynomial" kelimesinin köken bilgisi. Sıkıştırılmış Oxford İngilizce Sözlüğü
- ^ a b Edwards, Harold M. (1995). Linear Algebra (İngilizce). Springer. s. 47. ISBN 9780817637316. 2 Ocak 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 11 Aralık 2013.
- ^ Salomon, David (2006). Coding for Data and Computer Communications (İngilizce). Springer. s. 459. ISBN 9780387238043. 2 Ocak 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 11 Aralık 2013.
- ^ a b c Barbeau, E.J. (2003). Polynomials (İngilizce). Springer. ss. 1-2. ISBN 9780387406275. 28 Mart 2016 tarihinde kaynağından arşivlendi. Erişim tarihi: 13 Eylül 2020.
- ^ Barbeau, E.J. (2003). Polynomials (İngilizce). Springer. ss. 64-65. ISBN 9780387406275. 2 Ocak 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 11 Aralık 2013.