Bir üçgen düzlemde birbirine doğrusal olmayan üç noktayı birleştiren üç doğru parçasının birleşimidir. Üçgene müselles ve üçbucak da denir.
Altın oran, matematikte iki miktardan büyük olanın küçüğe oranı, miktarların toplamının miktarları büyük olanına oranı ile aynı ise altın orandır. Altın oran aynı zamanda antik çağdan bu yana sanat ve mimaride en iyi uyum ve oranları veren düzen bağıntısı olarak kabul edilmekteydi.
Alan veya yüz ölçümü, bir yüzeyin uzayda kapladığı iki boyutlu yer miktarını ölçen bir büyüklüktür. SI birim sisteminde temel alan birimi metrekaredir (m²). Diğer alan birimleri bundan türetilebilir:
- Ar = 100 metrekare (m²)
- Dekar = 1000 metrekareye (m²)
- Hektar = 10.000 metrekare (m²)
- Kilometrekare = 1.000.000 metrekare (m²)

Keops Piramidi, Khufu Piramidi ya da Büyük Piramit; günümüzde Mısır’ın başkenti Kahire'nin bir parçası olan Gize'yi çevreleyen antik “Gize mezar kenti”nde bulunan üç anıtsal piramitten en eski ve en büyük olanıdır. MÖ 2551-2560 yılları civarında yapıldığı sanılan bu anıtsal kompleks, Dünyanın yedi harikasından biri olup, bu yedi harika içinde günümüze kadar ulaşan tek eserdir.

Koni, matematikte, bir düzlem içindeki dairenin her noktasını, düzlem dışındaki bir noktaya birleştiren doğru parçalarının meydana getirdiği geometrik şekil.

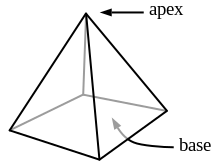
Piramit dış yüzeyleri üçgen olan ve üstte tek bir noktada birleşen ve şekli geometrik anlamda kabaca bir piramit halindeki bir yapıdır. Bir piramidin tabanı üçgen, dörtgen veya herhangi bir çokgen şekli olabilir. Bir piramit kütlesinin çoğunluğu yere yakın olup, daha az kütle tepedeki piramite doğru olur. Bunun nedeni, artan yükseklikle birlikte düşey eksen boyunca kesit alanının kademeli olarak azalmasıdır. Bu, ilk uygarlıkların anıtsal yapılar yaratmasına olanak tanıyan bir ağırlık dağılımı sundu. Dünyanın birçok yerindeki medeniyetler piramitler inşa etmişlerdir. Hacimce en büyük piramit, Meksika'nın Puebla eyaletindeki Orta Amerika Büyük Cholula Piramidi'dir. Binlerce yıl boyunca Dünya üzerindeki en büyük yapılar piramitlerdi. Mısır'daki Büyük Khufu Piramidi, Antik Dünyanın Yedi Harikası'nın günümüze ulaşan tek örneğidir.

Chichen Itza, Meksika'nın Yucatán Yarımadası'nda, Valladolid ve Mérida arasında yer alan, Kristof Kolomb öncesi dönemde kurulmuş bir İtza Maya kentidir. Muhtemelen bir dönem Yucatan'ın dini merkezi olmuştur. Günümüzde Meksika'nın en çok ziyaret edilen ikinci arkeolojik sit alanıdır. Chichen-Itza'daki El Castillo (kale) adıyla tanınan Kukulkan piramidinin yüksekliği üst platforma nazaran 24 m'dir. 7 Temmuz 2007'de seçilen dünyanın yeni yedi harikasından biridir. Efsaneye göre kent 10. yüzyılda Quetzalcoatl önderliğindeki Toltekler'ce alınmıştır. Kentteki önemli yapılar şunlardır:
- Kale adıyla tanınan Kukulkan Tapınağı ya da Kukulkan Piramidi: Mayalar bu piramidi astronomi ve matematik bilgilerini ortaya koymak istercesine belirli bir sistemle inşa etmişlerdir. Örneğin 4 cephesinin her birinde 91 basamak yer alır ki, böylece 4x91'le bulduğumuz 364 sayısına en tepedeki düzlüğü (1) de eklediğimizde yıldaki günlerin sayısı olan 365'i bulmaktayız. Ayrıca, piramidi öyle bir şekilde yönlendirmişlerdir ki, ilkbahar ve sonbaharda ekinoksların gerçekleştiği an, piramide gelen güneş ışıkları piramidin çıkıntıları sayesinde, merdiven basamaklarının dibinde bulunan iki yılan başı yontusunun S'ler çizen bir gövde uzantısı oluşacak şekilde bir gölge oluşturmaktadır. Bu yılan, Kukulkan adıyla bilinen ilah tüylü yılandır. Ayrıca piramiti inandıkları yeraltı alemi katları sayısı gibi 9 farklı düzey halinde düzenlemişlerdir. Piramidin tepesinden bakıldığında 300 hektarlık bir görüş alanına sahip olunur, yani kentteki tüm yapılar görülebilmektedir.
- Caracol denilen gözlemevi. Yapıya içindeki spiral taş merdiven nedeniyle olsa gerek, “salyangoz” anlamında bu ad verilmiştir.
- Adı Maya dilinde “esrarlı yazıların evi” anlamına gelen Akab Dzib
- Baş rahibin tapınağı.
- Savaşçılar Tapınağı.
- Top oyunu sahası.
- İspanyollarca “rahibeler manastırı” adı verilmiş yönetim sarayı.
- Çeşitli tapınakları içeren, “eski Chichen” yapılar grubu.

Vickers sertlik testi, malzemelerin sertliğini ölçmek için Brinell yöntemine alternatif olarak 1921 yılında Vickers Ltd tarafından geliştirilen yöntemdir.

Büyük Gize Sfenksi, Mısır'ın başkenti Kahire'de, Gize piramitleri bölgesinde yer alan bir sfenks heykelidir.

Louvre Piramidi, Paris'teki Louvre Müzesi'nin avlusunda bulunan cam ve metalden oluşturulmuş piramittir.

Gize Piramitleri Mısır'ın başkenti Kahire'nin Gize semtinde bulunan 3 görkemli yapı:
- Keops Piramidi
- Kefren Piramidi
- Mikerinos Piramidi

Geometride tetrahedron veya dört yüzlü, dört üçgen yüzden oluşan bir çokyüzlüdür (polihedron), her köşesinde üç üçgen birleşir. Düzgün dört yüzlü dört üçgenin eşkenar olduğu bir dört yüzlüdür ve Platonik cisimlerden biridir. Dörtyüzlü, dört yüzü olan tek konveks çokyüzlüdür. Tetrahedron isminin sıfat hali "tetrahedral"dır.
Prizma ya da biçme, genelde en boy ve yükseklik kavramlarına sahip cisimler olarak adlandırılır. Ancak bazı cisimlerin (küre) en ve boyu tam olarak ifade edilememekle çap ve çevre de bu nicelikleri belirtmek için kullanılır.

Kare piramit, tabanı kare olan ve tepe noktasını dört tane doğruyla birleştiren cisimlerdir.

Yükseklik cisimlerin referans alınan tabanından cismin tabana dik en uzak noktasıdır. Aynı zamanda yükseklik göreceli bir terimdir çünkü iki ve üç boyutlu cisimlerde değişebilmektedir. Bir örnek verecek olursak Bir kare piramidin yüksekliği tabanının(kare) merkezinden piramitin tepe noktasına çıkan bir doğru parçasıdır. Ancak yan yüzlerinin birindeki(üçgen) tabanından-ki bu taban iki boyutlu değildir bir boyutludur- tepesine bir dikme de yan yüz yüksekliği olarak tanımlanır.
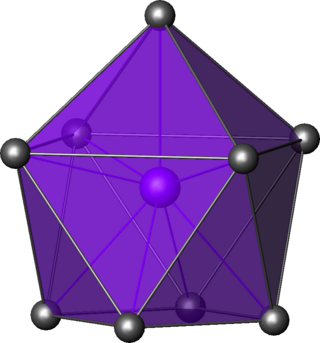
Kimyada, kepli kare antiprizmatik moleküler geometri, bir jiro-uzatılmış kare piramidin köşelerini tanımlayan dokuz atomun, atom gruplarının veya ligandların merkezi bir atomun etrafına yerleştirildiği bileşiklerin şeklini tanımlar.
Eski Mısır matematiği, Eski Mısır'da yaklaşık MÖ 3000 ila 300 yılları arasında, Eski Mısır Krallığı'ndan kabaca Helenistik Mısır'ın başlangıcına kadar geliştirilen ve kullanılan matematiktir. Eski Mısırlılar, saymak ve genellikle çarpma ve kesirleri içeren yazılı matematik problemlerini çözmek için bir sayı sistemi kullandılar. Mısır matematiğinin kanıtı, papirüs üzerine yazılmış, hayatta kalan az sayıda kaynakla sınırlıdır. Bu metinlerden, eski Mısırlıların, mimari mühendislik için yararlı olan üç boyutlu şekillerin yüzey alanını ve hacmini belirlemek gibi geometri kavramlarını ve sabit kesen yöntemi ve ikinci dereceden denklemler gibi cebir kavramlarını anladıkları bilinmektedir.
Thales teoremi veya temel orantı teoremi olarak da bilinen kesişme teoremi, kesişen iki çizginin bir çift paralelle kesilmesi durumunda oluşturulan çeşitli çizgi parçalarının oranları hakkındaki temel geometride önemli bir teoremdir. Benzer üçgenlerdeki oranlarla ilgili teoreme eşdeğerdir. Geleneksel olarak Yunan matematikçi Thales'e atfedilir.

Pappus'un alan teoremi, verilen herhangi bir üçgenin üç kenarına yaslanmış üç paralelkenarın alanları arasındaki ilişkiyi tanımlar. Pisagor teoreminin bir genellemesi olarak da düşünülebilecek teorem, adını onu keşfeden Yunan matematikçi İskenderiyeli Pappus'tan almıştır.