Pauling kuralı
Pauling'in kuralları,1929'da Linus Pauling tarafından iyonik bileşiklerin kristal yapılarını tahmin etmek ve rasyonelleştirmek için yayınlanan beş kuraldır.[1][2]
Birinci kural: Yarıçap oranı kuralı
Tipik iyonik katılar için katyonlar, anyonlardan daha küçüktür ve her katyon, bir polihedron (çok yüzeyli) oluşturan koordineli anyonlarla çevrilidir. Katyon-anyon mesafesi, yarıçaplarının toplamı ile belirlenmektedir.[3] İyonik yarıçapların toplamı katyon-anyon mesafesini belirlerken katyon-anyon yarıçap oranı (veya ) katyonun koordinasyon numarasını (KN) ve ayrıca anyonların koordineli polihedronunun şeklini belirlemektedir.[4][5]

Aşağıdaki tablodaki koordinasyon sayıları ve karşılık gelen çokyüzlüler için Pauling, iyonları katı küreler olarak kabul ederek katyonun verilen anyon sayısıyla temas halinde olduğu minimum yarıçap oranını matematiksel olarak türetmiştir.
| KN | Çokyüzlü | Yarıçap oranı |
|---|---|---|
| 3 | Üçgensel | 0.155 |
| 4 | Tetrahedron | 0.225 |
| 6 | Oktahedron | 0.414 |
| 7 | Başlıklı oktahedron | 0.592 |
| 8 | Kare antiprizma | 0.645 |
| 8 | Küp | 0.732 |
| 9 | Üçgen prizma | 0.732 |
| 12 | Küpoktahedron | 1.00 |
Katyon ve herhangi iki anyon bir dik üçgen oluşturmaktadır. veya . Sonra . Benzer geometrik kanıtlar oldukça simetrik KN = 3, 4 ve 8 durumları için minimum yarıçap oranlarını vermektedir.[6] KN = 6 ve minimumdan daha büyük bir yarıçap oranı için, katyon hala altı anyonla temas halinde olduğundan kristal daha kararlıdır ancak anyonlar birbirlerinden daha uzaktadır böylece karşılıklı itme azalmaktadır. Daha sonra 0.414'e eşit veya daha büyük bir yarıçap oranıyla bir oktahedron oluşabilmektedir ancak oran 0.732'nin üzerine çıktıkça kübik bir geometri daha kararlı hale gelmektedir. Bu, yarıçap oranı 0,55 olan NaCl'deki Na+'nın oktahedral koordinasyona sahip olmasına karşın, yarıçap oranı 0,93 olan CsCl'deki Cs+'nın kübik koordinasyona sahip olmasını açıklamaktadır.[7]

İkinci kural: Elektrostatik değerlik kuralı
Belirli bir katyon için, Pauling her bir koordineli anyonun elektrostatik bağ gücünü olarak tanımlamıştır. Burada z=katyon yükü, v=katyon koordinasyon sayısıdır. Lokal elektronötraliteyi korumak için kararlı bir iyonik yapı düzenlenmektedir böylece bir anyondaki elektrostatik bağların kuvvetlerinin toplamı o anyon üzerindeki yüke eşit olmaktadır.
| Katyon | Yarıçap oranı | Katyon KN | Elektrostatik bağ gücü | Anyon Kn |
|---|---|---|---|---|
| Li+ | 0.34 | 4 | 0.25 | 8 |
| Mg+2 | 0.47 | 6 | 0.33 | 6 |
| Sc+3 | 0.60 | 6 | 0.50 | 4 |
Üçüncü kural: Çokyüzlü köşelerin, kenarların ve yüzlerin paylaşımı
Kenarların ve özellikle yüzlerin iki anyon çokyüzlü tarafından paylaşılması iyonik bir yapının kararlılığını azaltmaktadır. Köşelerin paylaşılması stabiliteyi çok fazla azaltmaz bu nedenle örneğin oktahedra köşelerini birbirleriyle paylaşabilmektedir.[8]
Kararlılıktaki azalma, ortak kenarların ve yüzlerin katyonları birbirine daha yakın yerleştirmesinden ve böylece katyon-katyon elektrostatik itmesinin artmasından kaynaklanmaktadır. Etki, yüksek yüklü ve düşük KN'li katyonlar için en büyüktür.
Dördüncü kural: Farklı katyonlar içeren kristaller
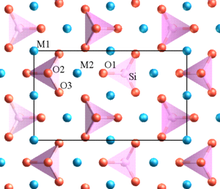
Farklı katyonlar içeren bir kristalde, yüksek değerlik ve küçük koordinasyon sayısına sahip olanlar, çokyüzlü elementleri birbirleriyle paylaşmama eğilimindedir.[9] Bu kural, aralarındaki elektrostatik itmeyi azaltmak için yüksek yüklü katyonlar arasındaki mesafeyi artırma eğilimindedir.Pauling'in örneklerinden biri olivin, M2SiO4'tür. Burada M bazı bölgelerde Mg2+ ve diğerlerinde Fe2+ karışımıdır. Yapı, herhangi bir oksijeni (köşelerde, kenarlarda veya yüzlerde) paylaşmayan farklı SiO4 tetrahedraları içermektedir. Düşük değerli Mg2+ ve Fe2+ katyonları oksijenleri paylaşan çokyüzlülerle çevrilidir.
Beşinci kural: Cimrilik kuralı
Bir kristaldeki esasen farklı türdeki bileşenlerin sayısı az olma eğilimindedir. Yinelenen birimler aynı olma eğiliminde olacaktır çünkü yapıdaki her atom belirli bir ortamda en kararlıdır. Dört yüzlü veya oktahedra gibi iki veya üç tür çokyüzlü olabilir, ancak çok farklı türler olmayacaktır.
Kaynakça
- ^ Pauling, Linus (1929). "THE PRINCIPLES DETERMINING THE STRUCTURE OF COMPLEX IONIC CRYSTALS". Journal of the American Chemical Society (İngilizce). 51 (4): 1010-1026. doi:10.1021/ja01379a006. ISSN 0002-7863. 15 Mayıs 2021 tarihinde kaynağından arşivlendi. Erişim tarihi: 22 Haziran 2021.
- ^ Pauling, Linus (1960). The nature of the chemical bond and the structure of molecules and crystals : an introduction to modern structural chemistry. Third edition. Ithaca, N.Y. ISBN 0-8014-0333-2. OCLC 545520.
- ^ "Pauling's Rules" (PDF). 24 Haziran 2021 tarihinde kaynağından (PDF) arşivlendi.
- ^ Pauling (1960) p.524.
- ^ Housecroft, Catherine E. (2005). Inorganic chemistry. 2nd ed. A. G. Sharpe. Upper Saddle River, N.J.: Pearson Prentice Hall. ISBN 0-13-039913-2. OCLC 56834315.
- ^ Yenilmez, Füsun; Kılıç, Esin (15 Ağustos 2018). "Türkiye'de İşgücüne Katılma Oranı-İşsizlik Oranı İlişkisi: Cinsiyet ve Eğitim Düzeyine Dayalı Bir Analiz". Eskişehir Osmangazi Üniversitesi İktisadi ve İdari Bilimler Dergisi. 13 (2): 55-76. doi:10.17153/oguiibf.410254. ISSN 1306-6730.
- ^ Petrucci, Ralph H. (2002). General chemistry : principles and modern applications. 8th ed. William S. Harwood, F. Geoffrey Herring. Upper Saddle River, N.J.: Prentice Hall. ISBN 0-13-014329-4. OCLC 46872308. 1 Temmuz 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 23 Haziran 2021.
- ^ Pauling (1960) p.559.
- ^ Pauling (1960), p.561.