Optik otokorelasyon

Optikte çeşitli otokorelasyon fonksiyonları deneysel olarak gerçekleştirilebilir. Yoğunluk otokorelasyon ve interferometrik otokorelasyon yaygın olarak kilitli lazerler tarafından üretilen ultra kısa darbelerin süresini tahmin etmek için kullanılır iken, alan otokorelasyonu ışık kaynağının spektrumunu hesaplamak için kullanılabilir. Lazer darbe süresi kolayca optoelektronik yöntemlerle ölçülemez çünkü fotodiodun ve osiloskopların tepki süreleri en iyi 200 femtosaniyelik mertebesindedir ancak lazer darbeleri ancak birkaç femtosaniyelik kadar kısa üretilebilmektedir.
Aşağıdaki örneklerde, otokorelasyon sinyali, ikinci harmonik oluşumu (SHG) tarafından lineear olmayan işlemlerle oluşturulur. Diğer teknikler iki-foton soğurma ilkesine dayanır ve otokolerasyon ölçümlerinde kullanılabilir,[1] bunun yanı sıra, yüksek dereceden doğrusal olmayan optik süreçleri gibi üçüncü harmonik üretimi, bu durumda matematiksel ifadelerin sinyal olacak biraz değiştirilmiş, ama bir otokolerasyon izinin temel yorumlanması aynı kalır. ayrıntılı bir tartışma, çok iyi bilinen kitaplarda yer almaktadır.[2][3]
Alan otomatik korelasyonu
Karmaşık bir elektrik alan E (t) için, saha otokorelasyon fonksiyonu ile tanımlanır
Bu Wiener-Khinchin teoremi bildiren Fourier dönüşümü alanında özilinti ise yelpazenin , yani, Kare büyüklüğünde olan Fourier dönüşüm . Bunun bir sonucu olarak, alan otokorelasyon spektral faz duyarlı değildir
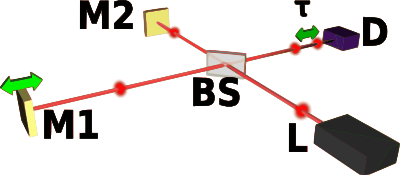
Alan otokorelasyon bir Michelson interferometrenin çıkışına bir yavaş dedektör konularak deneysel olarak ölçülür. Detektör bir koldan gelen giriş elektrik alan ve diğer koldan gelen gecikmiş kopya ile aydınlatılır. Eğer zaman yanıt dedektörü çok daha büyük bir zaman süresi sinyal veya kaydedilen sinyal entegre Dedektör tedbirleri yoğunluğu olarak taranan gecikme :
Genişleyen ortaya koyan bir hüküm olduğunu , kanıtlayan bir Michelson interferometre kullanılabilir için önlem alan, ortadan kaldırılması ya da spektrum (ve sadece spektrum). Bu ilke temelinde, Fourier dönüşümü spektroskopisi.
Yoğunluk otokorelasyonu
Yoğunluk otokorelasyonun optik uygulaması alan otokorelasyonu için olduğu kadar kolay değildir. Önceki kuruluma benzer şekilde, değişken bir gecikme ile iki paralel kirişler elde edilir; daha sonra, orantılı bir sinyal elde etmek üzere bir ikinci harmonik kristal'e odakanır (bkz: doğrusal olmayan optik) ile orantılı bir sinyal elde etmek için. Tek ışın yayma üzerindeki optik eksen oransal çapraz ürün , korudu. Bu sinyal daha sonra yavaş detektör tarafından kaydedilir
tam olarak otokorelasyonun yoğunluğu .
Kristallerde ikinci harmonik üretimi önceki kurulum aksine, yüksek tepe gücü gerektiren doğrusal olmayan bir süreçtir. Ancak, bu tür yüksek bir tepe gücü ultra kısa darbelerle sınırlandırılmış bir miktar enerji ile elde edilebilir ve bunun bir sonucu olarak otokorelasyonun yoğunluğu genellikle deneysel olarak ölçülür. Bu kurulum ile ilgili bir diğer zorluk ise ikinci harmonik oluşturulabilmesi için ışın demetlerinin kristalin içerisinde aynı noktaya odaklanmak zorunda olmalarıdır.
Bir darbe genişliğinde otokolerasyonun yoğunluğunun yoğunluğun genişliği ile ilişkili olduğu gösterilebilir.Gaussian zaman profili için otokolerasyon genişliği, yoğunluk genişliğinden kat daha uzundur ve bir hiperbolik sekant Kare (sech2) darbenin uzunluğundan 1.54 kat uzundur. Bu sayısal faktör, darbenin şekline bağlı, bazen dekonvolüsyon faktör olarak adlandırılır. Bu faktör, bilinen ya da kabul edilirse, bir darbe süresi (yoğunluk genişliği) bir yoğunluk otokorelasyon kullanılarak ölçülebilir. Ancak, faz ölçülemez.
İnterferometrik özilinti
Her iki önceki durumda bir arada olarak, doğrusal olmayan bir kristal eş-doğrusal geometride bir Michelson interferometre çıkışında ikinci harmonik üretmek için de kullanılabilir. Bu durumda, yavaş detektör tarafından kaydedilen sinyal;
interferometrik otokorelasyon denir. Spektral faz daha karmaşık hale geldikçe otokorelasyon izleme saçaklar yıkayın: Bu darbenin aşaması hakkında bazı bilgiler içermektedir.
Pupil otokorelasyon fonksiyonu
Bir optik sistemin optik transfer fonksiyonu T (a) olarak pupil fonksiyonu f (x, y) 'nin otokorelasyon ile verilmektedir:
Ayrıca bakınız
- Otomatik bağlayıcılar
- Sarım
- Optik yolluk düzeneğinin frekans çözümü
- Çok fotonlu iç itme girişim fazlı bir tarama
- Direkt elektrik alanın yeniden inşası için spektral faz enterforemetresi
Kaynakça
- ^ Roth, J. M., Murphy, T. E. & Xu, C. Ultrasensitive and high-dynamic-range two-photon absorption in a GaAs photomultiplier tube, Opt.
- ^ J. C. Diels and W. Rudolph, Ultrashort Laser Pulse Phenomena, 2nd Ed. (Academic, 2006).
- ^ W. Demtröder, Laserspektroskopie: Grundlagen und Techniken, 5th Ed. (Springer, 2007).



































