Matematik ; sayılar, felsefe, uzay ve fizik gibi konularla ilgilenir. Matematikçiler ve filozoflar arasında matematiğin kesin kapsamı ve tanımı konusunda görüş ayrılığı vardır.
Sayı, sayma, ölçme ve etiketleme için kullanılan bir matematiksel nesnedir. En temel örnek, doğal sayılardır. Sayılar, sayı adı (numeral) ile dilde temsil edilebilir. Daha evrensel olarak, tekil sayılar rakam adı verilen sembollerle temsil edilebilir; örneğin, "5" beş sayısını temsil eden bir rakamdır. Yalnızca nispeten az sayıda sembolün ezberlenebilmesi nedeniyle, temel rakamlar genellikle bir rakam sisteminde organize edilir, bu da herhangi bir sayıyı temsil etmenin organize bir yoludur. En yaygın rakam sistemi Hint-Arap rakam sistemidir, bu sistem on temel sayısal sembol, yani rakam kullanılarak herhangi bir negatif olmayan tam sayının temsil edilmesine olanak tanır. Sayılar sayma ve ölçme dışında, etiketlerde, sıralamada ve kodlarda kullanılmak için de sıklıkla kullanılır. Yaygın kullanımda, bir rakam ile temsil ettiği sayı net bir şekilde ayrılmaz.
Matematik felsefesinde, sezgicilik ya da yeni sezgicilik akımı, matematiğe insanların oluşturucu etkinliği olarak bakan bir yaklaşımdır.
Matematiğin temelleri olarak bilinen matematik dalı matematiğin tümü için geçerli olan en temel kavramları ve mantıksal yapıları inceler. Sayı, küme, fonksiyon, matematiksel tanıt, matematiksel tanım, matematiksel aksiyom, algoritma gibi kavramlar Matematiksel mantık, Aksiyomatik Küme Teorisi, Tanıtlama Teorisi, Model Teorisi, Hesaplama teorisi, Kategori Teorisi gibi yine matematiğim temelleri olarak anılan alanlarda incelenir. Bununla birlikte matematiğin temellerinin araştırılması matematik felsefesinin ana konularından biridir. Bu daldaki can alıcı soru matematiksel önermelerin hangi nihai esaslara göre "doğru" ya da "gerçek" kabul edilebileceğidir.
Modeller kuramı, matematiksel konseptleri küme kuramı temelinde inceleyen ya da başka bir deyişle matematiksel sistemlerin dayandığı modelleri araştıran matematik dalıdır. Modeller kuramı, 'dış dünyada' matematiksel nesnelerin var olduğunu varsayar ve nesneler, nesneler arasında bazı işlemler ya da bağıntılar ve bir aksiyomlar kümesi verildiğinde, nelerin nasıl tanıtlanabileceğine ilişkin sorular sorar.
Matematiksel ispat, matematiksel bir ifade için türetilmiş varsayımların mantıksal olarak doğru olduğu sonucunu garantileyen, çıkarımsal bir argümandır. Argüman, teoremler gibi önceden oluşturulmuş diğer ifadeleri kullanabilir; lakin prensipte her delil, kabul edilen çıkarım kurallarıyla birlikte yalnızca aksiyom olarak bilinen belirli temel veya orijinal varsayımlar kullanılarak oluşturulabilir.
İyi-sıralılık ilkesi, küme kuramının bir önermesidir. Her küme iyi sıralı bir küme yapılabilir. Bu teorem sonluötesi tümevarımın her kümede uygulanabilmesini sağlar. İyi sıralılık ilkesi seçim aksiyomuna denktir.
Matematikte reel sayılar kümesi, Fransızca réel “gerçek” den gelmektedir. Oranlı sayılar kümesinin evrim sürecinden elde edilen bir varsayım kombinasyonudur. Reel sayılar kümesi 
sembolüyle gösterilir.
Cebir sayılar teorisini, geometriyi ve analizi içine alan geniş bir matematik dalıdır. Temel matematik işlemlerinden, çember ve daire alanları bulmayı kapsayan geniş bir ilgi alanına sahiptir. Cebir, mühendislik ve eczacılık gibi birçok alanda kullanılmaktadır. Kuramsal cebir, ileri matematiğin bir dalı olmakla birlikte sadece uzmanlar tarafından çalışılan bir koldur.
Aritmetik; matematiğin sayılar arasındaki ilişkiler ile sayıların problem çözmede kullanımı ile ilgilenen dalı. Aritmetik kavramı ile genellikle sayılar teorisi, ölçme ve hesaplama kastedilir. Bununla birlikte bazı matematikçiler daha karmaşık çeşitli işlemleri de aritmetik başlığı altında değerlendirirler.
Soyut cebir veya soyut matematik, matematiğin bir alanı olup, cebirsel yapılar üzerinde çalışır. Cebirsel yapılar, elemanları üzerinde belirli işlemlerin uygulandığı kümelerdir ve gruplar, halkalar, alanlar, modüller, vektör uzayları, kafesler ve alan üzerindeki cebirler içerir. Soyut cebir terimi, 20. yüzyılın başlarında temel cebirden ayırmak amacıyla türetilmiştir. Soyut cebir ileri matematik için temel hale geldikçe basitçe "cebir" olarak adlandırılırken, "soyut cebir" terimi pedagoji dışında nadiren kullanılır.
Tüketerek tanıtlama veya kaba kuvvet yöntemi ya da durum çözümlemesi olarak bilinen yöntem, tanıtlanacak önermenin sonlu sayıda duruma bölünerek her durumun ayrı ayrı tanıtlandığı bir matematiksel tanıt yoludur. Tüketerek tanıtlama iki aşamada gerçekleştirilir:
- Durumların sonlu sayıda olduğunu gösteren bir tanıt verilir; yani tanıtlanacak olan önermenin her gerçeklemesinin durumlardan en az birinin koşullarına uyduğunu göstermek.
- Durumlardan her birini tanıtlamak.
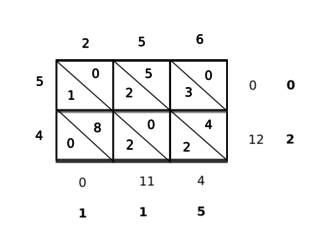
Çarpma, temel aritmetik işlemlerden biridir. Sayılarda çarpma, çarpılan sayının çarpan sayı kadar adedinin toplamının alınması işlemidir.
Cebirsel geometri, matematiğin bir dalıdır. Adından anlaşılabileceği gibi, soyut cebirin, özellikle değişmeli cebirin yöntemleri ile geometrinin dili ve problemlerini bir araya getirir. Çağdaş matematik içerisinde merkezi bir rol üstlenmesinin yanında, karmaşık analiz, topoloji, sayılar kuramı gibi matematiğin diğer dallarıyla yakın ilişkisi vardır.
Sonsuz küçükler, ölçülemeyecek kadar küçük cisimleri tarif etmek için kullanılır. Sonsuz küçüklerden yararlanmaktaki asıl amaç nicelik bakımından çok küçük olsalar da hala açı, eğim gibi belirli özelliklere sahip olmalarıdır. Sonsuz küçük kelimesi 17. Yüzyıl Modern Latin uydurma sözcüğü olan bir dizideki “sonsuzuncu” terim anlamına gelen infitesimustan gelmektedir. İlk olarak 1670 yılı civarında Nicolas Marecator ya da Gottfried Wilhelm Leibniz tarafından kullanılmıştır. Genel anlamla sonsuz küçük bir cisim herhangi bir uygulanabilir ölçümden küçük olan ama boyut olarak sıfırdan farklı ya da çok küçük olan ve bu nedenle sıfırdan ayırt edilemeyecek durumdaki cisimdir. Bundan dolayı sonsuz küçük ifadesi sıfat olarak kullanıldığında aşırı derecede küçük anlamına gelmektedir. Bir anlam verebilmek için genellikle aynı bağlamdaki başka bir sonsuz küçük ile karşılaştırılması gerekir. Sonsuz miktarda çok sonsuz küçük bir integral üretmek amacıyla toplanır. Arşimet “Mekanik Teoremlerin Metodu” adı verilen çalışmasında katı cisimlerin hacimlerini ve bölgelerin alanlarını bulmak için Bölünmezler Yöntemi olarak bilinen yöntemi kullanmıştır. Yayımlanan resmi bilimsel eserlerinde aynı problemleri Tüketme Yöntemi ile çözmüştür. 15. Yüzyılda Cusalı Nicholas’ın üzerinde çalıştığı bir çemberin alanını çemberi sonsuz kenarlı bir çokgen olarak hesaplama yöntemi 17. Yüzyılda Johannes Kepler tarafından geliştirilmiştir. Simon Stevin’in 16. Yüzyılda tüm sayıların ondalık gösterimi üzerine yaptığı çalışmalar gerçek sürekliliğe temel hazırladı. Bonaventura Cavalieri’nin bölünmezler yöntemi klasik yazarların sonuçlarını genişletmesine olanak sağladı. Bölünmezler yöntemi, eş boyutlu varlıklardan oluşan geometrik figürler ile ilişkilidir. John Wallis’in sonsuz küçük görüşü geometrik figürleri figürle aynı boyuta sahip sonsuz yapı bloğuna bölmesi ile bölünmezler yönteminden ayrılır. Bu görüş integral kalkülüsünün genel yöntemleri için temel hazırlamıştır. Sonsuz küçükleri alan hesabında 
ile göstermiştir. Leibniz tarafından kullanılan sonsuz küçükler, sonlu ve sonsuz sayılar için başarılı olan Süreklilik Kuramı ve belirlenemez miktarlar için gösterimi değiştirmenin yönteminin sadece belirlenebilir olanları göstererek yapılacağını anlatan Aşkın Homojenite Yasası gibi bulgusal prensiplere dayanmaktaydı. 18. Yüzyıl sonsuz küçüklerin Leonard Euler ve Joseph-Louis Lagrange gibi matematikçiler tarafından sıklıkla kullanıldığı bir zaman aralığı olmuştur. Augustin-Louis Cauchy sonsuz küçükleri Cour d’Analyse adlı eserinde sürekliliği açıklamak için ve Dirac delta fonksiyonunun ilk formlarından birini tanımlarken kullanmıştır. Tıpkı Cantor ve Dedekind’ın Stevin’in sürekliliğinin daha soyut bir halini geliştirdikleri gibi Paul du Bois-Reymond da sonsuz küçük ile zenginleştirilmiş süreklilik üzerine fonksiyonların artış oranını temel alan bir seri çalışma yapmıştır. Du Bois-Reymond’un çalışması Emile Boral ve Thoralf Skolem’ e ilham verdi. Borel Bois-Reymond’un çalışmalarını Cauchy’nin sonsuz küçüklerin artış oranına dair çalışmalarıyla bağlantı kurdu. Skolem 1934’te aritmetiğin standart dışı ilk modellerini geliştirdi. Süreklilik ve sonsuz küçük yasalarının matematiksel “implementasyonu” Abraham Robinson tarafından 1961’de yapılmıştır. Robinson ayrıca Edwin Hewirr’in 1948’de ve Jerzy Łoś’un 1955’teki çalışmalarına dayanarak standart dışı analizi geliştirmiştir. Hipergerçekler sonsuz küçük ile zenginleştirilmiş sürekliliği sağlar ve transfer prensibi de Leibniz’in süreklilik yasasını sağlar.
Tarih boyunca matematiğin konu çeşitliliği ve derinliği artmaktadır, matematiği kavrama, birçok konuyu matematiğin daha genel alanlarına göre sınıflandırma ve düzenleme için bir sistem gerektirir. Bir dizi farklı sınıflandırma şeması ortaya çıkmıştır ve bazı benzerlikleri paylaşsalar da, kısmen hizmet ettikleri farklı amaçlara bağlı olarak farklılıkları vardır. Ek olarak, matematik geliştirilmeye devam ettikçe, bu sınıflandırma şemaları da yeni oluşturulan alanları veya farklı alanlar arasında yeni keşfedilen bağlantıları dikkate alacak şekilde değişmelidir. Farklı alanlar arasındaki sınırı aşan, genellikle en aktif olan bazı konuların sınıflandırılması daha zor hale gelir.
Matematik, sayı, uzay, matematiksel yapı ve değişim gibi konuları araştıran bir çalışma alanıdır. Matematik ve bilim arasındaki ilişki hakkında daha fazla bilgi Matematik ve bilim bölümünde bulunabilir.
Matematik konularının listesi, matematik ile ilgili çeşitli konuları kapsar. Bu listelerden bazıları yüzlerce makaleye bağlantı içerir; bazıları sadece birkaç tane ile bağlantılıdır. Bu makale, aynı içeriği, göz atmaya daha uygun bir şekilde organize halde bir araya getirmektedir. Listeler, temel ve ileri matematik, metodoloji, matematiksel ifadeler, integraller, genel kavramlar, matematiksel nesneler ve referans tablolarının özelliklerini kapsar. Ayrıca insanların adını taşıyan denklemleri, matematiksel toplulukları, matematikçileri, matematik dergilerini ve meta listeleri de kapsar.
