Bir asal sayı, yalnızca 1'den büyük olup kendisinden küçük iki doğal sayının çarpımı olarak ifade edilemeyen bir doğal sayıdır. 1'den büyük ve asal olmayan doğal sayılara bileşik sayı adı verilir. Örneğin, 5 bir asal sayıdır çünkü onu bir çarpım olarak ifade etmenin mümkün olan yolları, 1 × 5 veya 5 × 1, yalnızca 5 sayısını içermektedir. Ancak, 4 bir bileşik sayıdır çünkü bu, her iki sayının da 4'ten küçük olduğu bir çarpım şeklindedir. Asal sayılar, aritmetiğin temel teoreminden ötürü sayı teorisi alanında merkezi öneme sahiptir: 1'den büyük her doğal sayı, ya bir asal sayıdır ya da asal sayıların çarpımı olarak, sıralamalarından bağımsız bir şekilde, benzersiz olarak çarpanlarına ayrılabilir.

Algoritma, belli bir problemi çözmek veya belirli bir amaca ulaşmak için tasarlanan yol. Matematikte ve bilgisayar biliminde bir işi yapmak için tanımlanan, bir başlangıç durumundan başladığında, açıkça belirlenmiş bir son durumunda sonlanan, sonlu işlemler kümesidir. Genellikle bilgisayar programlamada kullanılır ve tüm programlama dillerinin temeli algoritmaya dayanır. Aynı zamanda algoritma tek bir problemi çözecek davranışın, temel işleri yapan komutların veya deyimlerin adım adım ortaya konulmasıdır ve bu adımların sıralamasına dikkat edilmelidir. Bir problem çözülürken algoritmik ve sezgisel (herustic) olmak üzere iki yaklaşım vardır. Algoritmik yaklaşımda da çözüm için olası yöntemlerden en uygun olan seçilir ve yapılması gerekenler adım adım ortaya konulur. Algoritmayı belirtmek için; metinsel olarak düz ifade ve akış diyagramı olmak üzere 2 yöntem kullanılır. Algoritmalar bir programlama dili vasıtasıyla bilgisayarlar tarafından işletilebilirler.

Leonhard Euler, çizge teorisi çalışmasını kuran bir İsviçreli matematikçi, fizikçi, astronom, coğrafyacı, mantıkçı ve mühendisti. Topoloji ve analitik sayı teorisi, karmaşık analiz ve sonsuz küçük hesap gibi matematiğin diğer birçok dalında öncü ve etkili keşifler yaptı. Bir matematiksel fonksiyon kavramı da dahil olmak üzere, modern matematiksel terminolojinin ve gösterim'in çoğunu tanıttı. Ayrıca mekanik, akışkan dinamiği, optik, astronomi ve müzik teorisi alanındaki çalışmalarıyla da tanınır.
Alonzo Church, matematiksel mantığa ve teorik bilgisayar biliminin temellerine büyük katkılarda bulunan Amerikalı bir matematikçi ve mantıkçıydı. En çok, Entscheidungsproblem, Frege-Church ontolojisi ve Church-Rosser teoreminin çözülemezliğini kanıtlayan lambda kalkülüs, Church-Turing tezi ile tanınır. Ayrıca dil felsefesi üzerinde çalıştı.

Sudoku (Japonca: 数独, romanize: sūdoku, mantık tabanlı, kombinasyonel sayı yerleştirme bulmacasıdır. Klasik Sudoku, 9×9 boyutlarında bir diyagramda çözülen ve her satır, her sütun ve her 3×3'lük karede 1'den 9'a kadar rakamların birer kez yer almasını gerektiren sayı tabanlı bir zekâ oyunudur. Bulmaca hazırlayıcısı tek çözümü olması için iyi tasarlanmış belirli sayıları önceden kutucuklara yerleştirir.

Monty Hall problemi, Amerikan TV yarışma programı Let's Make a Deal'a dayanan bir olasılık bulmacasıdır. Problem adını, yarışmanın sunucusu Monty Hall'dan alır. İçinde bir paradoksu da barındırması nedeniyle Monty Hall paradoksu olarak da anılan problemin sonucu saçma görünmekle birlikte, ispatlanabilir ve doğrudur.

Yunan matematiği, Doğu Akdeniz kıyılarında MÖ 7. yüzyıldan MS 4. yüzyıla kadar uzanan Arkaik dönemden Helenistik ve Roma dönemlerine kadar yazılan matematik metinleri ile ortaya çıkan fikirleri ifade eder. Yunan matematikçiler, İtalya'dan Kuzey Afrika'ya tüm Doğu Akdeniz'e yayılmış şehirlerde yaşadılar, ancak kültür ve dil açısından birleştiler. "Matematik" kelimesinin kendisi Antik Yunancadan türemiştir: Grekçe: μάθημα: máthēma Yunanca telaffuz: [má.tʰɛː.ma] Yunanca telaffuz: [ˈma.θi.ma], "eğitim konusu" anlamına gelir. Kendi iyiliği için matematik çalışması ve genelleştirilmiş matematik teorilerinin ve kanıtlarının kullanılması, Yunan matematiği ile önceki uygarlıkların matematiği arasındaki önemli bir farktır.

Ernst Friedrich Ferdinand Zermelo, çalışmalarının matematiğin temelleri üzerinde büyük etkileri olan bir Alman mantıkçı ve matematikçiydi. Zermelo–Fraenkel aksiyomatik küme teorisini geliştirmedeki rolü ve iyi-sıralılık ilkesi için kanıtıyla tanınır. Ayrıca, 1929'da satranç oyuncularını sıralama üzerine çalışması, ikili karşılaştırma için bu yöntemi kullanan çeşitli uygulamalı alanlar üzerinde derin bir etkisi olmaya devam eden bir modelin ilk tanımıdır.

George David Birkhoff en çok, şu anda ergodik teorem olarak adlandırılan şeyle tanınan Amerikalı matematikçi. Birkhoff, döneminde Amerikan matematiğinin en önemli liderlerinden biriydi ve yaşadığı süre boyunca birçok kişi tarafından önde gelen Amerikalı bir matematikçi olarak kabul edildi.
Rönesans'tan bu yana, her yüzyılda, bir önceki göre daha fazla matematik problemi çözülmüştür. Yine de birçok büyük ve küçük problem çözüme kavuşturulamamıştır. Uzun süredir var olan bir sorunun çözümü için genellikle ödüller verilir ve çözülmemiş sorunların listeleri büyük önem kazanır. Çözülmemiş problemler, aralarında fizik, bilgisayar bilimi, cebir, matematiksel analiz, Kombinatorik, cebirsel geometri, ayrık geometri, Öklid geometrisi, katma ve cebirsel geometri teorileri, çizge teorisi, grup kuramı, modeller kuramı, sayılar teorisi, kümeler kuramı, Ramsey Kuramı, dinamik sistemler, Kısmi diferansiyel denklemler gibi birçok alanda varlığını sürdürmektedir.

İslam'ın Altın Çağı'nda matematik, özellikle 9. ve 10. yüzyıllarda, Yunan matematiği ve Hint matematiği üzerine inşa edilmiştir. Ondalık basamak-değer sisteminin ondalık kesirleri içerecek şekilde tam olarak geliştirilmesi, ilk sistematik cebir çalışması (Hârizmî tarafından yazılan Cebir ve Denklem Hesabı Üzerine Özet Kitap adlı eser ve geometri ve trigonometride önemli ilerlemeler kaydedilmiştir.
Eski Mısır matematiği, Eski Mısır'da yaklaşık MÖ 3000 ila 300 yılları arasında, Eski Mısır Krallığı'ndan kabaca Helenistik Mısır'ın başlangıcına kadar geliştirilen ve kullanılan matematiktir. Eski Mısırlılar, saymak ve genellikle çarpma ve kesirleri içeren yazılı matematik problemlerini çözmek için bir sayı sistemi kullandılar. Mısır matematiğinin kanıtı, papirüs üzerine yazılmış, hayatta kalan az sayıda kaynakla sınırlıdır. Bu metinlerden, eski Mısırlıların, mimari mühendislik için yararlı olan üç boyutlu şekillerin yüzey alanını ve hacmini belirlemek gibi geometri kavramlarını ve sabit kesen yöntemi ve ikinci dereceden denklemler gibi cebir kavramlarını anladıkları bilinmektedir.

Geometride adını Sakız Adalı Hipokrat'tan sonra alan Hipokrat ayı, iki çemberden oluşan yaylarla sınırlanmış bir aydır, daha küçük olanın çapı, daha büyük çember üzerinde dik bir açıyı kapsayan bir kirişe sahiptir.
William Lowell Putnam Matematik Yarışması, genellikle Putnam Yarışması olarak kısaltılır, Amerika Birleşik Devletleri ve Kanada'daki yüksek öğrenim kurumlarına kaydolan lisans üniversite öğrencileri için öğrencilerin milliyetlerinden bağımsız olarak düzenlenen yıllık bir matematik yarışmasıdır. En iyi öğrenciler için 250 ila 2.500 ABD Doları ve en iyi okullar için 5.000 ila 25.000 ABD Doları arasında değişen bir burs ve nakit ödüller dağıtılır, ayrıca, en iyi beş bireysel golcüden biri, Harvard Üniversitesi'nde 12.000 $'a kadar bir burs ve öğrenim ücreti alır, en iyi 100 bireysel puan sahibinin isimleri American Mathematical Monthly'de belirtilir ve ilk 500 yarışmacının isimleri ve adresleri katılan tüm kurumlara postalanır. Yaygın olarak dünyadaki en prestijli üniversite düzeyinde matematik yarışması olarak kabul edilir ve zorluğu, matematikte uzmanlaşan öğrenciler tarafından denenmesine rağmen medyan puanın genellikle sıfır olacağı şekildedir.

Élie Joseph Cartan, ForMemRS Lie grupları, diferansiyel sistemler ve diferansiyel geometri teorisinde temel çalışmalar yapan etkili bir Fransız matematikçi. Ayrıca genel göreliliğe ve dolaylı olarak kuantum mekaniğine önemli katkılarda bulundu. Yirminci yüzyılın en büyük matematikçilerinden biri olarak kabul edilmektedir.
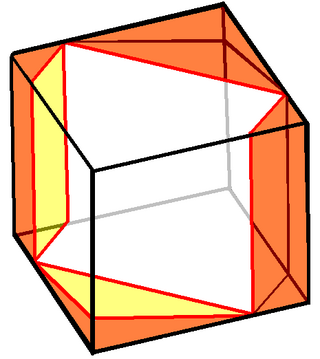
Prince Rupert'ın küpü, geometride, bir birim küp içine tüm boyunca kesilmiş bir delikten geçebilen en büyük küptür. Yani kenarları 1 birim uzunlukta olan bir küpten, küpü iki parçaya bölmeden geçebilir. Yan uzunluğu, içinden geçtiği birim küpünkinden yaklaşık %6 daha büyüktür. Tamamen bir birim küp içinde yer alan en büyük kareyi bulma sorunu ile çok yakından ilişkilidir ve aynı çözüme sahiptir.

Amerika Matematik Derneği (MAA), lisans düzeyinde erişilebilir matematiğe odaklanan profesyonel bir topluluktur. Üyeler arasında üniversite, kolej ve lise öğretmenleri; yüksek lisans ve lisans öğrencileri; saf ve uygulamalı matematikçiler; bilgisayar bilimcileri; istatistikçiler ve akademiden, hükûmetten, iş dünyasından ve endüstriden diğer birçok katılımcı yer almaktadır.
Uzun süredir devam eden ve henüz bir çözümü bulunamamış birçok matematikte çözülmemiş problemler vardır. John Tukey'e göre, "Sorunların tanımlanmasındaki güçlükler, istatistiği sorunların çözümündeki güçlüklerden çok daha fazla geciktirmiştir." "Bir veya iki açık problem" listesi David Cox tarafından verilmiştir.

Çemberin kareleştirilmesi veya Dairenin kareleştirilmesi, ilk olarak Yunan matematiğinde gündeme gelen bir geometri problemidir. Bir pergel ve çizgeç ile sadece sonlu sayıda adım kullanarak verilen bir dairenin alanı ile eş bir kare inşa etme uğraşısıdır. Problemin zorluğu, Öklid geometrisi'nin çizgiler ve dairelerin varlığına ilişkin aksiyomlarının böyle bir karenin varlığını gerektirip gerektirmediği sorusunu gündeme getirdi.
Newcomb paradoksu Felsefe ve matematikte,aynı zamanda Newcomb problemi olarak da bilinir. Biri geleceği tahmin edebilen iki oyuncu arasındaki oynanan bir oyunu konu edinen bir düşünce deneyidir.