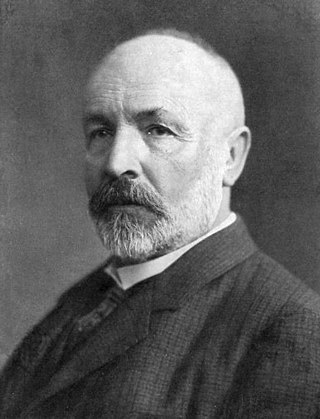Naif küme teorisi - Turkipedia

Naif küme teorisi, 19. yüzyılın sonlarında geliştirilen orijinal küme teorisidir. Bu teori, bir kümenin bazı ortak özelliklerle birleştirilen farklı şeylerin bir koleksiyonu olarak düşünülmesini sağlar. Ayrık matematikten zaten bilinen örneğin, bir kümede hangi öğelerin bulunduğunu gösteren Venn diyagramları veya Boole cebiri gibi kavramların çoğu kullanılır. Saf küme teorisindeki ciddi kusurların (Russel paradoksu gibi) keşfine yanıt olarak geliştirilen aksiyomatik küme teorisi ile karıştırılmamalıdır. Çağdaş matematik ve mühendisliğin birçok alanı için yeterince güçlüdür.^[1]

Naif küme teorisi bir dizi soruna yol açar:

1897'de keşfedilen Burali-Forti paradoksu nedeniyle tüm sıra sayıları kümesini oluşturmak mümkün değildir.
Cantor paradoksu'nda gösterildiği gibi (Birinci Cantor paradoksu) tüm kardinal sayıların kümesini oluşturmak mümkün değildir.
Her şeyin veya kümelerin kümesini oluşturmak mümkün değildir. Cantor paradoksunun ikincisinde gösterildiği gibi (1899'da keşfedildi).
Kendilerini içermeyen tüm kümelerin kümesi, 1902'de keşfedilen Russell paradoksu'nu oluşturur.

Yukarıdaki tüm problemler ancak aksiyomlar, kümeleri ve özelliklerini tanımlamak için kullanılabildiğinde problem olarak gösterilebilir.

Richard Dedekind (1831-1916) bu durumu keşfetti ve 1888'de yeni bir küme teorisi başlattı. Keşfettiği küme teorisinde kümeler hakkında aksiyomlar vardır. Ancak onun aksiyomatik küme teorisi de yine de yeterince iyi değildir çünkü:

Tüm sonlu ondalık sayılar kümesi, 1905'te keşfedilen Richard paradoksuna yol açar.
Tüm sonlu doğal sayılar kümesi, 1908'de keşfedilen Berry paradoksunu gösterir.
Sahip olmadıkları bir özelliği tanımlayan tüm kelimelerin kümesine, 1908'de keşfedilen Grelling-Nelson paradoksu denir.

Kaynakça

^ "Categorical algebra and set-theoretic foundations", Axiomatic Set Theory (Proc. Sympos. Pure Math., Vol. XIII, Part I, Univ. California, Los Angeles, Calif., 1967), Amer. Math. Soc., Providence, R.I., 1971, ss. 231-240 . "The working mathematicians usually thought in terms of a naïve set theory (probably one more or less equivalent to ZF) ... a practical requirement [of any new foundational system] could be that this system could be used "naïvely" by mathematicians not sophisticated in foundational research" (p. 236).

Kaynaklar

Bourbaki, N.
Cantor, Georg (1874), "Ueber eine Eigenschaft des Inbegriffes aller reellen algebraischen Zahlen", J. Reine Angew. Math., 1874 (77), ss. 258-262, doi:10.1515/crll.1874.77.258, 4 Haziran 2012 tarihinde kaynağından arşivlendi, erişim tarihi: 19 Haziran 2023, See also pdf version
Frege, Gottlob (1893), Grundgesetze der Arithmetik, 1, Jena
Halmos, Paul (1960). Naive Set Theory. Princeton, NJ: D. Van Nostrand Company.
- Halmos, Paul (1974). Naive Set Theory (Reprint bas.). New York: Springer-Verlag. ISBN 0-387-90092-6.
- Halmos, Paul (2011). Naive Set Theory (Paperback bas.). Mansfield Centre, CN: D. Van Nostrand Company. ISBN 978-1-61427-131-4.
Jech, Thomas (2002). Set theory, third millennium edition (revised and expanded). Springer. ISBN 3-540-44085-2.
Kelley, J.L., General Topology, Van Nostrand Reinhold, New York, NY, 1955.
van Heijenoort, J. 0-674-32449-8.
Meschkowski, Herbert; Nilson, Winfried (1991), Georg Cantor: Briefe. Edited by the authors., Berlin: Springer, ISBN 3-540-50621-7
Peano, Giuseppe (1889), Arithmetices Principies nova Methoda exposita, Torino
Zermelo, Ernst (1932), Georg Cantor, Berlin: Springer

Dış bağlantılar

Beginnings of set theory 28 Ekim 2019 tarihinde Wayback Machine sitesinde arşivlendi.
Earliest Known Uses of Some of the Words of Mathematics (S) 3 Kasım 2017 tarihinde Wayback Machine sitesinde arşivlendi.

İlgili Araştırma Makaleleri

<span class="mw-page-title-main">Matematik</span> nicelik, yapı, uzay ve değişim gibi konularla ilgilenen bilim dalı

Matematik ; sayılar, felsefe, uzay ve fizik gibi konularla ilgilenir. Matematikçiler ve filozoflar arasında matematiğin kesin kapsamı ve tanımı konusunda görüş ayrılığı vardır.

Doğal sayılar, $\text{[math]}$ şeklinde sıralanan tam sayılardır ve kimi tanımlamalara göre 0 sayısı da bu kümeye dâhil edilebilir. Aralarında standart ISO 80000-2'nin de bulunduğu bazı tanımlar doğal sayıları $0$ ile başlatır ve bu durum negatif olmayan tam sayılar için $0, 1, 2, 3, ...$ şeklinde bir karşılık bulurken, bazı tanımlamalar $1$ ile başlamakta ve bu da pozitif tam sayılar için $1, 2, 3, ...$ şeklinde bir eşlenik oluşturur. Doğal sayıları sıfır olmadan ele alan metinlerde, sıfırın da dahil edildiği doğal sayılar bazen tam sayılar olarak adlandırılırken diğer bazı metinlerde bu terim, negatif tam sayılar da dahil olmak üzere tam sayılar için kullanılmaktadır. Özellikle ilkokul seviyesindeki eğitimde, doğal sayılar, negatif tam sayıları ve sıfırı dışlamak ve saymanın ayrık yapısını, gerçek sayıların bir karakteristiği olan ölçümün sürekliliğiyle karşıtlık oluşturmak amacıyla sayma sayıları olarak adlandırılabilir.

Kümeler teorisi ile şunlar kastedilmiş olabilir:

Kümeler kuramı; Alman matematikçi Georg Cantor'un 1874-1895 yılları arasında geliştirdiği, 20. yüzyıl matematiğinin temelini oluşturan teori.
Zermelo-Freankel küme kuramı (ZFC); basit kümeler kuramındaki Russel paradoksu gibi zafiyetlere yanıt olarak geliştirilen, aksiyoma (belit) dayalı bir kuram.

Eksiklik Teoremi, Kurt Gödel'in 1931 yılında doktorasında yer verdiği "Principia Mathematica Gibi Dizgelerin Biçimsel Olarak Karar Verilemeyen Önermeleri Üzerine" başlıklı makalesinde 4. önerme olarak geçer. Sezgisel olarak matematikte belitlere (aksiyom) dayanan her sistemin tutarlı olması dahilinde eksik olması gerektiğini bildirir.

Öklid geometrisi, İskenderiyeli Yunan matematikçi Öklid’e atfedilen matematiksel bir sistemdir ve onun Elemanlar adlı geometri üzerine ders kitabında tarif edilmektedir. Öklid'in yöntemi, sezgisel olarak çekici küçük bir aksiyom seti varsaymaktan ve bu aksiyomlara dayanarak birçok başka önermeyi (teoremleri) çıkarmaktan ibarettir. Öklid'in sonuçlarının çoğu daha önceki matematikçiler tarafından ifade edilmiş olsa da, Öklid, bu önermelerin kapsamlı bir tümdengelimli ve mantıksal sisteme nasıl uyabileceğini gösteren ilk kişi oldu. Elemanlar, ilk aksiyomatik sistem ve resmi ispatın ilk örnekleri olarak ortaokulda (lise) hala öğretilen düzlem geometrisi ile başlar. Üç boyutlu katı geometrisi ile devam ediyor. Elemanlar’ın çoğu, geometrik dilde açıklanan, şimdi cebir ve sayı teorisi olarak adlandırılan şeyin sonuçlarını belirtir.

Georg Ferdinand Ludwig Philipp Cantor, Alman matematikçi. Kümeler kuramının kurucusudur. Kümeler arasında birebir eşlemenin önemini ortaya koydu, "sonsuz küme" kavramına matematiksel bir tanım getirdi ve gerçel sayıların sonsuzluğunun doğal sayıların sonsuzluğundan "daha büyük" olduğunu ispatladı. Ayrıca kardinal sayı ve ordinal sayı kavramlarını ortaya atmış ve bu sayıların aritmetiğini tanımlamıştır. Cantor'un buluşlarının matematik ve felsefede önemli yeri vardır.

Julius Wilhelm Richard Dedekind, sayılar teorisi, soyut cebir konularına önemli katkılarda bulunan bir Alman matematikçiydi. En iyi bilinen katkısı, Dedekind kesimi kavramı aracılığıyla reel sayıların tanımıdır. Ayrıca modern küme teorisi ve Mantıkçılık' olarak bilinen matematik felsefesi'nin gelişiminde öncü olarak kabul edilir.

Küme, matematikte farklı nesnelerin topluluğu veya yığını olarak tanımlanmaktadır. Bu tanımdaki "nesne" soyut ya da somut bir şeydir. Fakat her ne olursa olsun iyi tanımlanmış olan bir şeyi, bir eşyayı ifade etmektedir. Örneğin, "Tüm canlılar topluluğu", "Dilimiz alfabesindeki harflerin topluluğu", "Masamın üzerindeki tüm kâğıtlar" tümcelerindeki nesnelerin anlaşılabilir, belirgin oldukları, kısaca iyi tanımlı oldukları açıkça ifade edilmektedir. Dolayısıyla bu tümcelerin her biri bir kümeyi tarif etmektedir. O halde, matematikte "İyi tanımlı nesnelerin topluluğuna küme denir." biçiminde bir tanımlama yapılmaktadır.

Kümeler teorisi, matematiğin, matematiksel nesneler olan kümeleri inceleyen dalıdır. Neredeyse bütün matematik kümeler kuramının kendi dilinde ifade edilebilir. Alman matematikçi Georg Cantor tarafından 1874 ile 1895 yılları arasında geliştirilen ve daha sonrasında, Ernst Zermelo, Kurt Gödel gibi 20. yüzyılın oldukça tanınmış matematikçileri tarafından aksiyomatikleştirilen teoridir.

Cantor teoremi, kümeler teorisinin başlıca teoremlerindendir. Teorem; boş olmayan herhangi bir X kümesinin kuvvet kümesinin kardinalitesinin, X kümesinin kardinalitesinden büyük olduğunu söyler. P(X) ile kuvvet kümesi gösterilirse, teoreme göre X kümesi ile P(X) arasında birebir eşleme yapılamaz.

Ernst Friedrich Ferdinand Zermelo, çalışmalarının matematiğin temelleri üzerinde büyük etkileri olan bir Alman mantıkçı ve matematikçiydi. Zermelo–Fraenkel aksiyomatik küme teorisini geliştirmedeki rolü ve iyi-sıralılık ilkesi için kanıtıyla tanınır. Ayrıca, 1929'da satranç oyuncularını sıralama üzerine çalışması, ikili karşılaştırma için bu yöntemi kullanan çeşitli uygulamalı alanlar üzerinde derin bir etkisi olmaya devam eden bir modelin ilk tanımıdır.

<span class="mw-page-title-main">İki parçalı graf</span>

Graf teorisinde, düğümleri her kenar iki kümede de birer bitiş ucuna sahip olacak şekilde iki ayrı kümeye ayrılabilen graflara iki parçalı graf adı verilir.

Tarih boyunca matematiğin konu çeşitliliği ve derinliği artmaktadır, matematiği kavrama, birçok konuyu matematiğin daha genel alanlarına göre sınıflandırma ve düzenleme için bir sistem gerektirir. Bir dizi farklı sınıflandırma şeması ortaya çıkmıştır ve bazı benzerlikleri paylaşsalar da, kısmen hizmet ettikleri farklı amaçlara bağlı olarak farklılıkları vardır. Ek olarak, matematik geliştirilmeye devam ettikçe, bu sınıflandırma şemaları da yeni oluşturulan alanları veya farklı alanlar arasında yeni keşfedilen bağlantıları dikkate alacak şekilde değişmelidir. Farklı alanlar arasındaki sınırı aşan, genellikle en aktif olan bazı konuların sınıflandırılması daha zor hale gelir.

Matematikte graf ya da çizge, nesne çiftlerinin bir anlamda "ilişkili" olduğu bir dizi nesne kümesini belirleyen bir yapıdır. Nesneler, köşeler adı verilen matematiksel soyutlamalara karşılık gelir ve ilgili düğüm çiftlerinin her birine bir kenar, ayrıt adı verilir. Tipik olarak bir graf, kenarları için çizgiler veya eğriler ile birleştirilen, düğümler için bir nokta veya daire kümesi olarak diyagram şeklinde gösterilir. Graflar ayrık matematikte çalışmanın amaçlarından biridir.

Matematiğin temellerinde, 1901'de Bertrand Russell tarafından keşfedilen Russell Paradoksu, Georg Cantor tarafından yaratılan sezgisel kümeler kuramının resmileştirilmesinin bazı girişimlerin bir çelişkiye yol açtığını gösterdi. Aynı paradoks 1899'da Ernst Zermelo tarafından da keşfedilmişti ancak Zermelo, sadece David Hilbert, Edmund Husserl ve Göttingen Üniversitesi'nin diğer üyeleri tarafından bilinen fikri yayınlamadı. 1890'ların sonunda Cantor, tanımının Hilbert ve Richard Dedekind'e mektupla söylediği bir çelişkiye yol açacağını fark etmişti.

Makalenin kısa özeti; farklı nesnelerin koleksiyonları olarak kümeler hakkında konuşur, matematikte birçok kullanımları olduğunu ve matematiğin set teorisinde kodlanabileceğini ve matematiğin çoğunu yapmak için yeterince küme teorisinin aksiyomatize edilebileceğini belirtir. Konunun aksiyomları veya amaçlanan yorumu ile tanımlanıp tanımlanmadığı konusunda tarafsız kalır. Antinomilerden bahsedilirse, aksiyomatizasyonun çözüm olduğunu iddia etmemeli, ancak bazılarının onları aksiyomatizasyon ile çözüldüğünü, diğerleri de kümülatif hiyerarşi ile değerlendirdiğini belirtmelidir. -> Venn diyagramı, ikisinin set matematik Kümeleri. Küme teorisi, gayri resmi olarak nesne koleksiyonları olan matematiksel mantığın ' kümeleri üzerinde çalışan bir dalıdır. Herhangi bir nesne türü bir kümede toplanabilse de, küme teorisi çoğunlukla matematikle ilgili nesnelere uygulanır. Küme teorisinin dili neredeyse tüm matematiksel nesne leri tanımlamak için kullanılabilir.

Matematik, sayı, uzay, matematiksel yapı ve değişim gibi konuları araştıran bir çalışma alanıdır. Matematik ve bilim arasındaki ilişki hakkında daha fazla bilgi Matematik ve bilim bölümünde bulunabilir.

Matematiksel analizde, küme üzerindeki bir ölçü, bu kümenin her bir uygun alt kümesine bir sayı atamanın sistematik bir yoludur ve sezgisel olarak kümenin boyutu olarak yorumlanır. Bu anlamda ölçü, uzunluk, alan ve hacim kavramlarının bir genellemesidir. Özellikle önemli bir örnek, Öklid geometrisinin geleneksel uzunluğunu, alanını ve hacmini $n$ -boyutlu Öklid uzayının $R n$ uygun alt kümelerine atayan bir Öklid uzayındaki Lebesgue ölçüsüdür. Örneğin, gerçek sayılardaki $[0, 1]$ aralığının Lebesgue ölçüsü, kelimenin günlük anlamındaki uzunluğudur ve tam olarak 1'dir.

Felix Hausdorff, modern topolojinin kurucularından biri olarak kabul edilen ve küme teorisine, tanımlayıcı küme teorisine, ölçü teorisine ve fonksiyonel analize önemli katkılarda bulunan bir Alman matematikçi.

İlginç sayı paradoksu, doğal sayıları "ilginç" ya da "sıradan" olarak sınıflandırma girişiminden doğan mizahi bir paradokstur. Paradoks, her doğal sayının ilginç olduğunu belirtir. Bu ifadenin "ispatı", çelişki yöntemiyle yapılır: Sıradan doğal sayıların kümesi boş değilse bu kümenin en küçük elemanı, "en küçük sıradan sayı" olma özelliğine sahip olduğu için ilginç bir sayı olur. Bu durumun yarattığı çelişki nedeniyle, sıradan doğal sayıların kümesi boş küme olmalıdır.

Bu sayfa, bu Vikipedi makalesine dayanmaktadır.
Metin, CC BY-SA 4.0 lisansı altında mevcuttur; ek koşullar uygulanabilir.
Görseller, videolar ve sesler kendi lisansları altında mevcuttur.