Moskova Papirüsü

Moskova Matematik Papirüsü, Mısır dışındaki ilk sahibi olan Eski Mısır bilimci Vladimir Golenishchev'in ardından Golenishchev Matematik Papirüsü olarak da adlandırılan eski bir Mısır matematik papirüsüdür. Golenishchev papirüsü 1892 veya 1893'te Teb'de satın alındı. Daha sonra bugün kaldığı Moskova'daki Puşkin Devlet Güzel Sanatlar Müzesi koleksiyonuna girdi.

Hiyeratik (Resim yazısı ile yazılmış) metnin paleografisine (eski yazı bilimi) ve ortografisine (yazım ve imlasına) dayanarak, metin büyük olasılıkla 13. Hanedanlığa yazılmıştır ve muhtemelen Mısır'ın 12. Hanedanlığı'na, kabaca MÖ 1850'ye tarihlenen daha eski materyallere dayanmaktadır.^[1] Yaklaşık 5½ m (18 ft) uzunluğunda ve 3,8 ile 7,6 cm (1,5 ve 3 inç) arasında değişen genişlikte sayfa düzeni, 1930'da^[2] Sovyet Doğubilimci Vasily Vasilievich Struve^[3] tarafından çözümlerle 25 probleme bölünmüştür. İyi bilinen matematiksel bir papirüstür ve genellikle Rhind Papirüsü ile birlikte anılır. Moskova Matematik Papirüsü, Rhind Papirüsü'nden daha eski ancak daha küçüktür.^[4]

Moskova Papirüsündeki problemler, belirli bir sırayı takip etmez ve problemlerin çözümleri Rhind Papirüs'ündekinden çok daha az ayrıntı sağlar. Papirüs, bazı geometri problemleriyle tanınır. Problem 10 ve 14, sırasıyla bir yüzey alanını ve bir kesik kısmın hacmini hesaplamakla ilgilidir. Geri kalan sorunlar doğada daha yaygındır.^[1]

2. ve 3. problemler, geminin parçası problemleridir. Problemlerden biri, bir geminin dümeninin uzunluğunu hesaplarken diğeri, orijinal olarak 30 arşın uzunluğunda bir sedir kütüğünün uzunluğunun 1/3 + 1/5'i olan bir gemi direğinin uzunluğunu hesaplar.^[1]

Aha problemleri, miktarı ve parçalarının toplamı verilen bilinmeyen miktarları (Aha olarak anılır) bulmayı içerir. Rhind Papirüsü ayrıca bu tür problemlerden dördünü içerir. Moskova Papirüsünün 1, 19 ve 25. problemleri Aha problemleridir. Örneğin 19. problem, birinden 1 ve ½ kez alınan ve 10 yapmak için 4'e eklenen bir miktarın hesaplanmasını ister.^[1] Başka bir deyişle, modern matematiksel gösterimde birinden ${\displaystyle {\frac {3}{2}}x+4=10}$ denklemini çözmesi istenir.

Problemlerin çoğu pefsu problemleridir (bakınız: Mısır cebiri): 25 problemden 10'u. Bir pefsu, tahıl hekat'ından (antik Mısır hacim birimi) yapılan biranın gücünü ölçer:

${\displaystyle {\mbox{pefsu}}={\frac {\mbox{somun ekmek (veya sürahi bira) sayısı}}{\mbox{tahıl hekat sayısı}}}}$

(1) pefsu 20'nin 100 somun ekmek hesaplama örneği (2) Biri size: "pefsu 20'nin 100 somun ekmeğiniz var (3) pefsu 4 birası ile değiştirilmek için (4) 1/2 1/4 maltlık bira gibi" (5) Önce pefsu 20'nin 100 somun ekmeği için gerekli olan tahıl miktarını hesaplayın (6) Sonuç 5 hekattır. O zaman 1/2 1/4 maltlık bira denilen biradan bir sürahi bira için neye ihtiyacınız olduğunu düşünün (7) Sonuç, Yukarı Mısır tahılından yapılan sürahi birası için gereken hekat ölçüsünün 1/2'sidir. (8) 5 hekatın 1/2'sini hesaplayın, sonuç 2 1/2 olacaktır (9) Bunu 2 1/2 dört kez al (10) Sonuç 10'dur. Sonra ona şöyle dersiniz: (11) "Bakın! Bira miktarının doğru olduğu görülüyor."^[1]

11. ve 23. problemler Baku problemleridir. Bunlar, işçilerin çıktısını hesaplar. Problem 11, bir kişinin 5'e 5 ölçülerinde 100 kütük getirdiği durumda, buna karşılık 4'e 4 ölçülerde kaç kütük getirebileceğini sorar. Problem 23, sandaletleri kesmesi ve süslemesi gereken bir kunduracının çıkarttığı işi bulur.^[1]

Yirmi beş problemin yedisi geometri problemleridir ve üçgenlerin alanlarını hesaplamadan bir yarım kürenin yüzey alanını (problem 10) ve kesik bir piramitin hacmini bulmaya kadar uzanır.^[1]

Moskova Matematik Papirüsünün 10. problemi, bir yarım kürenin (Struve, Gillings) veya muhtemelen bir yarım silindirin (Peet) yüzey alanının hesaplanmasını ister. Aşağıda, sorunun bir yarım kürenin alanıyla ilgili olduğunu varsayıyoruz.

Problem 10'un metni şu şekilde çalışır: "Bir sepet hesaplama örneği. Size ağzı 4 1/2 olan bir sepet verilir. Bunun yüzeyi nedir? Sepet, yarım yumurta kabuğu gibi olduğu için 9'un 1/9'unu alın. 1 bulursun. Kalanı hesaplayın, 8 bulunurr. 8'in 1/9'unu hesaplayın. 2/3 + 1/6 + 1/18 elde edersiniz. 2/3 + 1/6 + 1/18'i çıkardıktan sonra bu 8'in kalanını bulun. 7 + 1/9 bulursun. 7 + 1/9'u 4 + 1/2 ile çarpın. 32 bulursun. Bakın burası onun alanıdır. Doğru buldunuz."^[1][5]

Çözüm, alanı şu şekilde hesaplamaktır: ${\displaystyle {\text{Alan}}=\left({\frac {2\times 8}{9}}\right)^{2}\times ({\text{çap}})^{2}={\frac {256}{81}}({\text{çap}})^{2}}$

Bu, Moskova Papirüsünü yazanın ${\displaystyle {\frac {256}{81}}\approx 3.16049}$'u yaklaşık π değeri olarak kullandığı anlamına gelir.

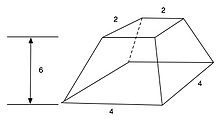
Moskova Matematiksel Papirüsü'nün 14. problemi, bir kesik cismin (frustum) hacmini hesaplar.

Problem 14, bir piramidin, gösterildiği gibi üst alanın 2 birim uzunluğunda bir kare, alt tarafın 4 birim uzunluğunda bir kare ve yüksekliğinin 6 birim olacağı şekilde kesildiğini belirtir. Hacmin 56 kübik birim olduğu görülmüştür ki bu doğrudur.^[1]

Örneğin metni şu şekilde çalışır: "Size söylenirse: dikey yüksekliği 6'dan oluşan kesilmiş bir piramit, dikey yükseklik için tabanda 4, üstte 2: 4'ün karesini alacaksınız; sonuç 16. 4'ü ikiye katlayacaksınız; sonuç 8. Bu 2'nin karesini alacaksınız; sonuç 4. 16'yı, 8'i ve 4'ü eklemelisiniz; sonuç 28. 6'nın 1/3'ünü alacaksınız; sonuç 2. 28'i iki kez alacaksınız; sonuç 56. Bak, bu 56. [Onu] doğru bulacaksın."^[6]

Problemin çözümü, Mısırlıların kesik bir piramidin hacmini elde etmek için doğru formülü bildiklerini gösteriyor:

${\displaystyle V={\frac {1}{3}}h(a^{2}+ab+b^{2})}$

a ve b, kesik piramidin taban ve üst kenar uzunlukları ve h, yüksekliği olmak üzere. Araştırmacılar, Mısırlıların kesik bir cismin (frustum) hacmi formülüne nasıl ulaşmış olabileceklerini tahmin etmişlerdir, ancak bu formülün türetilmesi papirüste verilmemiştir.^[7]

Richard J. Gillings, Papirüs'ün içeriğinin üstünkörü bir özetini verdi^[8] Üstü çizili sayılar, payda olarak bu sayıya sahip birim kesri belirtir. örneğin; ${\displaystyle {\bar {4}}={\frac {1}{4}}}$; birim kesirler eski Mısır matematiğinde ortak çalışma nesneleriydi.

Moskova Matematik Papirüsünün İçeriği^[a]

No.	İçerik detayı.
1	Hasarlı ve okunamaz durumda.
2	Hasarlı ve okunamaz durumda.
3	Bir sedir direği. ${\displaystyle 30}$'un ${\displaystyle {\bar {3}}\;{\bar {5}}}$'i ${\displaystyle =16}$. Belirsiz.
4	Bir üçgenin alanı. ${\displaystyle 4\times 10}$'un ${\displaystyle {\bar {2}}}$'si ${\displaystyle =20}$.
5	Somun ve ekmek pesusu. No. 8'e benzer.
6	Dikdörtgen, Alan ${\displaystyle =12,b={\bar {2}}\;{\bar {4}}l}$. ${\displaystyle l}$ ve ${\displaystyle b}$'yi bul.
7	Üçgen, Alan ${\displaystyle =20,h=2\;{\bar {2}}b}$. ${\displaystyle h}$ ve ${\displaystyle b}$'yi bul.
8	Somun ve ekmek pesusu.
9	Somun ve ekmek pesusu.
10	Yarım kürenin (veya silindirin) eğimli yüzey alanı.
11	Somun ve sepet. Belirsiz.
12	Bira pesusu. Belirsiz.
13	PSomun ve ekmek pesusu. No. 9'a benzer.
14	Kesik bir piramidin hacmi. ${\displaystyle V=(h/3)(a^{2}+ab+b^{2})}$.
15	Bira pesusu.
16	Bira pesusu. No. 15'e benzer.
17	Üçgen, Alan ${\displaystyle =20,b=({\bar {3}}\;{\bar {15}})h}$. ${\displaystyle h}$ ve ${\displaystyle b}$'yi bul.
18	Kıyafetlerin arşın ve avuç içi ile ölçümü. Belirsiz.
19	Denklemi çözün, ${\displaystyle 1\;{\bar {2}}x+4=10}$. Net.
20	${\displaystyle 1,000}$ somun pesusu. Horus-gözü kesirleri.
21	Kurbanlık ekmeğin karıştırılması.
22	Somun ve bira pesusu. Takas.
23	Bir ayakkabı tamircisinin işini hesaplamak. Belirsiz. Peet çok zor der.
24	Somun ve bira takası.
25	Denklemi çözün, ${\displaystyle 2x+x=9}$. Basit ve net.

Eski Mısır'dan diğer matematiksel metinler şunları içerir:

• Berlin Papirüsü 6619
• Mısır Matematiksel Deri Rulosu
• Lahun Matematiksel Papirüsü
• Rhind Papirüsü

1. ^ Bu tablo, Gillings'in "Firavunlar Zamanında Matematik (İngilizce: Mathematics in the Time of the Pharoahs)", ss. 246-247'nin kelimesi kelimesine bir kopyasıdır. Yalnızca diğer bölümlere yapılan atıflar atlanmıştır. Pesu problemleri hakkındaki 5, 8-9, 13, 15, 20-22 ve 24 numaralı problemlerin açıklamalarının bilgileri "Bkz. Bölüm 12" ile sonuçlanmıştır. Doğrusal ve ikinci dereceden denklemler hakkındaki problem 19'un açıklamasının bilgileri "Bkz. Bölüm 14" ile sonuçlanmıştır. Yarım silindirlerin veya yarım kürelerin yüzey alanları hakkındaki problem 10 ve 14'ün açıklamalarının bilgileri "Bkz. Bölüm 18" ile sonuçlanmıştır.

• Struve, Vasilij Vasil'evič, and Boris Turaev. 1930. Mathematischer Papyrus des Staatlichen Museums der Schönen Künste in Moskau. Quellen und Studien zur Geschichte der Mathematik; Abteilung A: Quellen 1. Berlin: J. Springer

• Allen, Don. Nisan 2001. The Moscow Papyrus27 Mart 2018 tarihinde Wayback Machine sitesinde arşivlendi. and Summary of Egyptian Mathematics3 Mart 2016 tarihinde Wayback Machine sitesinde arşivlendi..
• Imhausen, A., Ägyptische Algorithmen. Eine Untersuchung zu den mittelägyptischen mathematischen Aufgabentexten, Wiesbaden 2003.
• Mathpages.com. The Prismoidal Formula31 Ocak 2020 tarihinde Wayback Machine sitesinde arşivlendi..
• O'Connor and Robertson, 2000. Mathematics in Egyptian Papyri12 Ocak 2012 tarihinde Wayback Machine sitesinde arşivlendi..
• Truman State University, Math and Computer Science Division. Mathematics and the Liberal Arts: Ancient Egypt18 Şubat 2013 tarihinde Wayback Machine sitesinde arşivlendi. and The Moscow Mathematical Papyrus13 Mayıs 2012 tarihinde Wayback Machine sitesinde arşivlendi..
• Williams, Scott W. Mathematicians of the African Diaspora5 Temmuz 2020 tarihinde Wayback Machine sitesinde arşivlendi., containing a page on Egyptian Mathematics Papyri7 Nisan 2015 tarihinde Wayback Machine sitesinde arşivlendi..
• Zahrt, Kim R. W. Thoughts on Ancient Egyptian Mathematics27 Eylül 2011 tarihinde Wayback Machine sitesinde arşivlendi..