Morfogenezin Kimyasal Temelleri

"Morfogenezin Kimyasal Temelleri" İngiliz matematikçi Alan Turing'in 1952 yılında yazdığı bir makaledir.^[1] Doğadaki çizgiler ve spiraller gibi desenlerin homojen, tekdüze bir durumdan doğal olarak nasıl ortaya çıkabileceğini açıklamaktadır. Morfogenezin reaksiyon-difüzyon teorisi olarak adlandırılabilecek teori, teorik biyolojide temel bir model haline gelmiştir.^[2] Bu tür örüntüler Turing örüntüleri olarak bilinmektedir. Örneğin, VEGFC proteininin zebra balığı embriyosunda lenfatik damarların oluşumunu yönetmek için Turing kalıpları oluşturabileceği varsayılmıştır.^[3]

Reaksiyon-difüzyon sistemleri

Reaksiyon-difüzyon sistemleri örüntü oluşumu için bir prototip model olarak çok ilgi çekmiştir. Cepheler, spiraller, hedefler, altıgenler, şeritler ve dağıtıcı solitonlar gibi örüntüler, örneğin yerel reaksiyon terimlerindeki büyük tutarsızlıklara rağmen çeşitli reaksiyon-difüzyon sistemlerinde bulunur. Bu tür örüntüler "Turing örüntüleri" olarak adlandırılmıştır.^[4]

Reaksiyon-difüzyon süreçleri, hayvan postlarının embriyonik gelişimi ve deri pigmentasyonu için bir açıklama sınıfı oluşturur.^[5]^[6] Reaksiyon-difüzyon sistemlerine olan ilginin bir başka nedeni de, doğrusal olmayan kısmi diferansiyel denklemleri temsil etmelerine rağmen, genellikle analitik bir tedavi için olasılıkların olmasıdır.^[7]^[8]^[9]

Ayrıca bakınız

Evrimsel gelişim biyolojisi

Kaynakça

^ Turing, Alan (1952). "The Chemical Basis of Morphogenesis" (PDF). Philosophical Transactions of the Royal Society of London B. 237 (641). ss. 37-72. Bibcode:1952RSPTB.237...37T. doi:10.1098/rstb.1952.0012. JSTOR 92463. 1 Mart 2021 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 1 Ocak 2024.
^ Harrison, L.G. (1993). Kinetic Theory of Living Pattern. Cambridge University Press.
^ Wertheim, Kenneth (2019). "Can VEGFC form turing patterns in the Zebrafish embryo?". Bulletin of Mathematical Biology. 81 (4): 1201-1237. doi:10.1007/s11538-018-00560-2. PMC 6397306 $2. PMID 30607882.
^ Wooley, T. E., Baker, R. E., Maini, P. K., Chapter 34, Turing's theory of morphogenesis. In Copeland, B. Jack; Bowen, Jonathan P.; Wilson, Robin; Sprevak, Mark (2017). The Turing Guide. Oxford University Press. ISBN 978-0198747826.
^ Meinhardt, H. (1982). Models of Biological Pattern Formation. Academic Press.
^ Murray, James D. (9 Mart 2013). Mathematical Biology. Springer Science & Business Media. ss. 436-450. ISBN 978-3-662-08539-4.
^ Grindrod, P. Patterns and Waves: The Theory and Applications of Reaction-Diffusion Equations, Clarendon Press (1991)
^ Smoller, J. Shock Waves and Reaction Diffusion Equations, Springer (1994)
^ Kerner, B. S. and Osipov, V. V. Autosolitons. A New Approach to Problems of Self-Organization and Turbulence, Kluwer Academic Publishers (1994).

İlgili Araştırma Makaleleri

Tasarım desenleri, tasarım kalıpları, tasarım örüntüleri veya tasarım şablonları, çok rastlanan, birbirine benzer sorunları çözmek için geliştirilmiş ve işlerliği kanıtlanmış genel çözüm önerileridir.

<span class="mw-page-title-main">Apiaceae</span>

Apiaceae, Apiales takımına bağlı bir bitki familyasıdır.

<span class="mw-page-title-main">Gérard Debreu</span> Amerikalı matematikçi (1921-2004)

Gérard Debreu, Fransız asıllı fakat 1975'te ABD vatandaşlığına geçmiş olan bir matematikçi ve iktisatçı. 1962'de Kaliforniya Üniversitesi, Berkeley'ye iktisat profesörü olarak atanıp ün yapmıştır. 1983'te Nobel Ekonomi Ödülü'nü kazanmıştır.

Reinhard Selten, Nobel ödüllü Alman ekonomist.

Ernst denklemi, matematik'te doğrusal-olmayan bir kısmi diferansiyel denklem'dir.

Temsil teorisi soyut cebirdeki cebirsel yapıları, daha somut olan matematiksel nesnelerin dönüşümleri olarak tasvir etmeye çalışan bir matematik dalıdır. Örneğin soyut bir $\text{[math]}$ grubunu bir vektör uzayı $\text{[math]}$ 'nin eşyapı dönüşüm grubunun( $\text{[math]}$ ) içinde görmeye çalışır. Böyle temsillere doğrusal temsil denir, çünkü bu temsil aslında $\text{[math]}$ grubundan genel lineer grup $\text{[math]}$ 'ye bir morfizma yazmak demektir. Böyle bir temsil bulmaktaki amaç, $\text{[math]}$ grubunu çalışmak için lineer cebir kullanmaktır. Soyut gruplardaki çarpma işlemi, özellikle bir bilgisayar için matris çarpmasından daha zordur. Soyut bir grubun doğrusal temsillerini kullanarak, gruptaki kimi hesaplamaları bilgisayara yaptırmak daha kolay olur.

Elektron optiği, elektronların elektromanyetik alanlarda izledikleri yörüngelerin hesaplanmasında kullanılan matematiksel yapıdır. Elektron optiği hesaplamaları, elektron mikroskopları ve parçacık hızlandırıcılarda kullanılmaktadır.

<span class="mw-page-title-main">János Aczél</span> Macar-Kanadalı matematikçi (1924-2020)

János Dezső Aczél, aynı zamanda John Aczel olarak bilinen fonksiyonel denklemler ve bilgi teorisi konusunda uzmanlaşmış Macar-Kanadalı matematikçi.

Trioksidan, hidrojen trioksit veya dihidrojen trioksit olarak da adlandırılan, H[O]₃H (H₂O₃ olarak da yazılır) kimyasal formülüne sahip bir inorganik bileşiktir. Kararsız hidrojen polioksitlerdendir. Sulu çözeltilerde, trioksidan su ve tekli oksijen oluşturmak için ayrışır:

Vladimir İgoreviç Arnold Sovyet-Rus matematikçi. En iyi entegre sistemlerin stabilitesi ile ilgili Kolmogorov-Arnold-Moser teoremi ile tanınmasına rağmen, dinamik sistem teorisi, cebir, felaket teorisi, topoloji, cebirsel geometri, sezgisel geometri, diferansiyel denklemler, klasik mekanik dahil olmak üzere birçok alanda önemli katkılarda bulunmuştur., Hidrodinamik ve tekillik teorisi, ADE sınıflandırma problemini ortaya çıkarmak da dahil olmak üzere, ilk ana sonucundan bu yana - 19 yaşında 1957'de Hilbert'in on üçüncü probleminin çözdü. İki yeni matematik dalı kurdu: KAM teorisi ve topolojik Galois teorisi öğrencisi Askold Hovanskiy ile).

<span class="mw-page-title-main">Matematiksel ve teorik biyoloji</span>

Matematiksel ve teorik biyoloji, biyolojinin bilimsel teorileri kanıtlamak için gerekli deneyleri yapmakla uğraşan deneysel biyoloji dalının aksine biyolojik sistemlerin yapılarının, gelişimlerinin ve davranışlarının altında yatan ilkeleri araştırmak için yaşayan organizmaların teorik analizlerini, matematiksel modellerini ve soyutlamalarını kullanan bir dalıdır. Bu alan aynı zamanda matematiksel yanını vurgulamak için matematiksel biyoloji ya da biyomatematik ya da biyolojik yanını vurgulamak için ise teorik biyoloji olarak da adlandırılır. Teorik biyolojinin odak noktası daha çok biyolojinin teorik ilkelerinin geliştirilmesi iken matematiksel biyoloji biyolojik sistemlerin incelenmesinde matematiği kullanır ama her iki terim de bazen birbirinin yerine kullanılabilmektedir.

Kimyasal reaksiyon mühendisliği, kimya mühendisliği ve endüstriyel kimya alanında kullanılan kimyasal reaktörler ve tepkime kinetiği ile ilgilenen bir uzmanlık alanıdır. Tepkime kinetiği ve reaktör tasarımını birleştiren kimyasal reaksiyon mühendisliği, birçok endüstriyel kimyasalın üretimi için gerekli temel bir unsurdur. Kimyasal reaksiyon mühendisliği disiplininin günlük hayatta pek çok uygulama alanı bulunur. Kimyasal üretimi, ilaç üretimi ve atık arıtımı faaliyetlerinde reaksiyon mühendisliği kullanılır. Enzim kinetiği, farmakokinetik, ısı etkileri, ani reaksiyonlar ve tesis güvenliği gibi konularda da kimyasal reaksiyon mühendisliği disiplininden faydalanılır. Kimyasal reaksiyon mühendisliği ilk kez 1940'lar ve 1950'lerde hızla büyüyen kimya ve petrokimya sanayisinin ihtiyaçlarını karşılamak için ortaya çıkmış ve günümüze kadar plastiklerin, kimyasalların, ilaçların ve diğer pek çok maddenin üretim süreçlerinde kullanılan bir yöntem olmuştur.

Geometride, Theodorus Sarmalı, uç uca yerleştirilmiş dik üçgenlerden oluşan bir spiraldir. Adını, Cyreneli Theodorus'tan almıştır.

<span class="mw-page-title-main">Israel Gelfand</span> Sovyet matematikçi (1913 – 2009)

Israel Moyseyovich Gelfand, Yahudi asıllı ünlü bir Sovyet matematikçisiydi. Grup teorisi, temsil teorisi ve fonksiyonel analiz dahil olmak üzere matematiğin birçok dalına önemli katkılarda bulundu. Lenin Nişanı ve ilk Kurt Ödülü de dahil olmak üzere birçok ödülün sahibi, Kraliyet Cemiyeti'nin Yabancı Üyesi ve Moskova Devlet Üniversitesi'nde profesördü ve 76. doğum gününden kısa bir süre önce Rutgers Üniversitesi'nde Amerika Birleşik Devletleri'ne göç etti ve yaşamının sonuna dek orada kaldı.

Leonard Eugene Dickson, Amerikalı bir matematikçiydi. Soyut cebir, özellikle sonlu alanlar ve klasik gruplar teorisi alanındaki ilk Amerikalı araştırmacılardan biriydi ve aynı zamanda üç ciltlik bir sayılar teorisi tarihi kitabı ile hatırlanmaktadır.

Tekli sayı sistemi, doğal sayıları temsil eden en basit sayı sistemidir: bir N sayısını temsil etmek için, 1'i temsil eden bir simge N kez tekrarlanır.

Floquet teorisi, periyodik katsayılı doğrusal diferansiyel denklem sistemlerinin çözümü ile ilgilenen bir matematik alt dalıdır. Floquet teorisi,

\text{[math]}

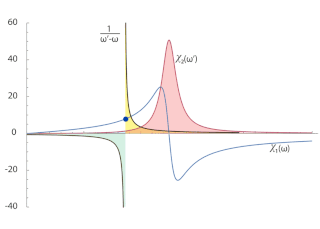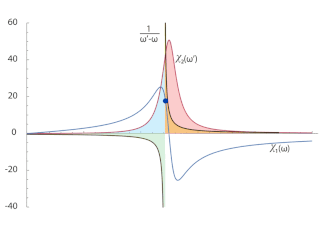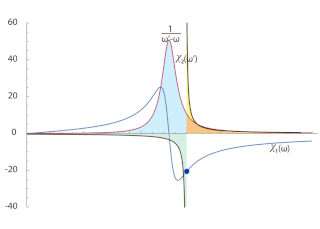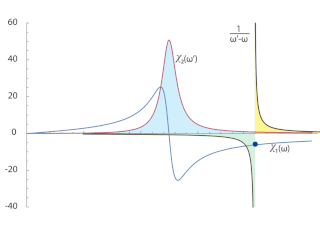
<span class="mw-page-title-main">Kramers-Kronig ilişkileri</span>

Karmaşık analiz ve fizikte Kramers-Kronig ilişkileri, üst yarı düzlemde analitik olan herhangi bir karmaşık fonksiyonun reel ve sanal kısımlarını iki yönlü bir şekilde ilişkilendirir. Bu ilişkiler genellikle doğrusal fiziksel sistemlerin tepki fonksiyonlarının reel kısmı aracılığıyla sanal kısmının elde edilmesinde kullanılır; aynı şekilde sanal kısım aracılığı ile reel kısım da bu şekilde elde edilebilir. Bu ilişkiler, stabil fiziksel sistemlerdeki nedenselliği belirtir. Bu ilişkiler ismini fizikçiler Hendrik Anthony Kramers ile Ralph Kronig'den almaktadır.

<span class="mw-page-title-main">Jean-Pierre Vigier</span> Fransız fizikçi (1920 – 2004)

Jean-Pierre Vigier, fiziğin temelleri, özellikle kuantum fiziğinin stokastik yorumu üzerine yaptığı çalışmalarla tanınan bir Fransız teorik fizikçidir.

Matematik sosyolojisi, hem sosyolojik araştırmalarda matematiğin kullanımıyla hem de matematik ile toplum arasında var olan ilişkilerin araştırılmasıyla ilgilenen disiplinler arası bir araştırma alanıdır.

Bu sayfa, bu Vikipedi makalesine dayanmaktadır.
Metin, CC BY-SA 4.0 lisansı altında mevcuttur; ek koşullar uygulanabilir.
Görseller, videolar ve sesler kendi lisansları altında mevcuttur.