Mie saçılması

Mie saçılması veya Mie teorisi, düzlem bir elektromanyetik dalganın (ışık) homojen bir küre tarafından saçılmasını ifade eder. Maxwell denklemlerinin Lorenz–Mie–Debye çözümü olarak da bilinmektedir. Denklemlerin çözümü sonsuz bir vektör küresel harmonik serisi şeklinde yazılır. Saçılma ismini fizikçi Gustav Mie'den almaktadır; analitik çözümü ilk kez 1908 yılında yayınlanmıştır.^[1]

"Mie saçılması" terimi aynı zamanda ışığın dalga boyunun kürenin yarıçapı ile yaklaşık eşit olduğu saçılma durumları için de kullanılmaktadır; bu saçılma özellikle atmosferde görülür. Genel Mie saçılmasının teknik olarak bir boyut limiti yoktur: saçılma sonuçları kürenin dalga boyundan küçük olduğunu durumlarda Rayleigh saçılmasına, büyük olduğu özel durumlarda ise geometrik optiğe yakınsar. Mie saçılması ve tesir kesitinin hesaplanması için birçok kod bulunmaktadır; Mie teorisinin konsentrik küreler, sonsuz silindir ve küre kümelerine uygulandığı kodlar da mevcuttur.

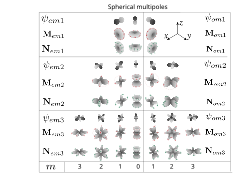
Mie saçılmasında çarpan ve saçılan elektrik alanlar vektör küresel harmonikleri olarak yazılır. Helmholtz denkleminin küresel koordinat sisteminde değişkenlerin ayrımı ile çözülmesi ile elde edilir. Kürenin yüzeyinde elektromanyetik sınır koşulları sağlanarak saçılan dalga farklı katsayılarda çok kutuplu harmonikler cinsinden gösterilir. Işık saçılma oranı genellikle optik tesir kesiti ile ifade edilir ve bu katsayı Mie saçılması ile elde edilebilir.^[1][2] Teori kullanarak Mie rezonansları ve saçılma katsayıları da bulunabilmektedir.^[3]

Işığın dalga boyunun kürenin yarıçapına oranına ve malzeme özelliklerine göre farklı yaklaşım ve tanımlamalarda bulunulabilir. Rayleigh saçılması dalga boyundan çok daha küçük parçacıklardaki ışık saçılmasını belirtir.^[1] Bu dalga boyları için yarı-statik yaklaşım kullanılarak Laplace denklemi de çözülebilir.^[4] Rayleigh–Gans yaklaşımı ve ayrıksı kırınım teorisi (van de Hulst yaklaşımı) parçacığın kırılma indisinin bulunduğu ortamınkine çok yakın olduğu durumlarda kullanılabilir. Yaklaşımlar her ne kadar birçok uygulamada iş görse de atmosferdeki su damlacıklarındaki, hücrelerdeki ve emülsiyonlardaki saçılmaların hesaplanması için tam teorinin kullanılması esastır.^[1]

Mie saçılmasının standart analitik çözümü genelde z-ekseninde hareket eden ve x-ekseninde polarize olmuş bir düzlem dalga için yapılır. Parçacığın yalıtkanlık sabiti ve manyetik geçirgenliği ${\displaystyle \varepsilon _{1}}$ ve ${\displaystyle \mu _{1}}$ ile gösterilirken, parçacığın bulunduğu ortamdaki değerler ${\displaystyle \varepsilon }$ ve ${\displaystyle \mu }$ ile gösterilir.^[1]

Saçılma probleminin çözümü için öncelikle vektör Helmholtz denklemi küresel koordinatlarda yazılır. Helmholtz denklemi, elektrik ve manyetik alanlar için şu şekilde gösterilir:^[5]

${\displaystyle \nabla ^{2}\mathbf {E} +{k}^{2}\mathbf {E} =0,\ \ \ \ \nabla ^{2}\mathbf {H} +{k}^{2}\mathbf {H} =0}$

Helmholtz denklemi dışında, alanların ${\displaystyle \nabla \cdot \mathbf {E} =\nabla \cdot \mathbf {H} =0}$, ${\displaystyle \nabla \times \mathbf {E} =i\omega \mu \mathbf {H} }$ ve ${\displaystyle \nabla \times \mathbf {H} =-i\omega \varepsilon \mathbf {E} }$ koşullarını sağlaması gerekir. Daha sonra ${\displaystyle \mathbf {M} }$ ve ${\displaystyle \mathbf {N} }$ küresel harmoniklerinin üreten fonksiyonu olarak kabul edebileceğimiz skalar ${\displaystyle \psi }$ fonksiyonu denkleme eklenir; vektör küresel harmonikler gerekli koşulları sağlamaktadır.

Küresel koordinatlarda açılan dalga denklemi şu şekilde ifade edilebilir:

${\displaystyle {\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}\left(r^{2}{\frac {\partial \psi }{\partial r}}\right)+{\frac {1}{r^{2}sin\theta }}{\frac {\partial }{\partial \theta }}\left(sin\theta {\frac {\partial \psi }{\partial \theta }}\right)+{\frac {1}{r^{2}sin\theta }}\left({\frac {\partial ^{2}\psi }{\partial \phi ^{2}}}\right)+k^{2}\psi =0}$

Bu denklem değişkenlerin ayrımı yöntemi ile çözülür. Denklemin çözümüne göre üreten fonksiyonunu sağlayan vektör küresel harmonikler şu şekilde ifade edilir:

${\displaystyle \mathbf {M} _{^{e}_{o}mn}=\nabla \times \left(\mathbf {r} \psi _{^{e}_{o}mn}\right)}$ — manyetik harmonikler (TE)

${\displaystyle \mathbf {N} _{^{e}_{o}mn}={\frac {\nabla \times \mathbf {M} _{^{e}_{o}mn}}{\mathbf {k} }}}$ — elektrik harmonikler (TM)

ve

${\displaystyle {\psi _{emn}=\cos m\varphi P_{n}^{m}(\cos \vartheta )z_{n}({k}r)}}$

${\displaystyle {\psi _{omn}=\sin m\varphi P_{n}^{m}(\cos \vartheta )z_{n}({k}r)}}$

${\displaystyle P_{n}^{m}(\cos \theta )}$ Asosiye Legendre polinomlarını ve ${\displaystyle z_{n}({k}r)}$ ise küresel Bessel fonksiyonlarını gösterir.

Daha sonrasında küreye çarpan düzlem dalga vektör küresel harmonikler cinsinden açılır:^[5]

${\displaystyle \mathbf {E} _{inc}=E_{0}e^{ikr\cos \theta }\mathbf {e} _{x}=E_{0}\sum _{n=1}^{\infty }i^{n}{\frac {2n+1}{n(n+1)}}\left(\mathbf {M} _{o1n}^{(1)}(k,\mathbf {r} )-i\mathbf {N} _{e1n}^{(1)}(k,\mathbf {r} )\right)}$

${\displaystyle \mathbf {H} _{inc}={\frac {-k}{\omega \mu }}E_{0}\sum _{n=1}^{\infty }i^{n}{\frac {2n+1}{n(n+1)}}\left(\mathbf {M} _{e1n}^{(1)}(k,\mathbf {r} )+i\mathbf {N} _{o1n}^{(1)}(k,\mathbf {r} )\right)}$

Buradaki ${\displaystyle (1)}$ üst-imi ${\displaystyle \psi _{^{e}_{o}mn}}$ fonksiyonun radyal kısmının küresel Bessel fonksiyonu olduğunu belirtir. Açılım katsayıları ise şu integraller ile elde edilir:

${\displaystyle {\frac {\int _{0}^{2\pi }\int _{0}^{\pi }\mathbf {E} _{inc}\cdot \mathbf {M} _{^{e}_{o}mn}^{(1)}\sin \theta d\theta d\varphi }{\int _{0}^{2\pi }\int _{0}^{\pi }|\mathbf {M} _{^{e}_{o}mn}^{(1)}|^{2}\sin \theta d\theta d\varphi }}}$

${\displaystyle m\neq 1}$'ı sağlayan tüm katsayılar 0'dır.

Sonrasında şu koşullar çözümde göz önünde bulundurulur:

1. Kürenin yüzeyinde elektromanyetik sınır koşulları sağlanmalıdır.

1. Saçılma probleminin çözümü orijinde sınırlandırılmalıdır: bu nedenle kürenin içindeki alanların üreten fonksiyonu olarak küresel Bessel fonksiyonları seçilir.

1. Saçılan alan, orijinden sonsuza doğru hareket etmelidir; bunun için birinci tip Hankel fonksiyonları seçilir.

Saçılan alanlar, daha sonra vektör harmonik açılımla şu şekilde yazılır:

${\displaystyle \mathbf {E} _{s}=\sum _{n=1}^{\infty }E_{n}\left(ia_{n}\mathbf {N} _{e1n}^{(3)}(k,\mathbf {r} )-b_{n}\mathbf {M} _{o1n}^{(3)}(k,\mathbf {r} )\right)}$

${\displaystyle \mathbf {H} _{s}={\frac {k}{\omega \mu }}\sum _{n=1}^{\infty }E_{n}\left(a_{n}\mathbf {M} _{e1n}^{(3)}(k,\mathbf {r} )+ib_{n}\mathbf {N} _{o1n}^{(3)}(k,\mathbf {r} )\right)}$

Bu denklemlerde ${\displaystyle (3)}$ üst-imi ${\displaystyle \psi _{^{e}_{o}mn}}$ fonksiyonun radyal kısmının küresel Hankel fonksiyonu olduğunu belirtir.

Kürenin içindeki alanlar ise şu şekilde açılabilir:

${\displaystyle \mathbf {E} _{1}=\sum _{n=1}^{\infty }E_{n}\left(-id_{n}\mathbf {N} _{e1n}^{(1)}(k_{1},\mathbf {r} )+c_{n}\mathbf {M} _{o1n}^{(1)}(k_{1},\mathbf {r} )\right)}$

${\displaystyle \mathbf {H} _{1}={\frac {-k_{1}}{\omega \mu _{1}}}\sum _{n=1}^{\infty }E_{n}\left(d_{n}\mathbf {M} _{e1n}^{(1)}(k_{1},\mathbf {r} )+ic_{n}\mathbf {N} _{o1n}^{(1)}(k_{1},\mathbf {r} )\right)}$

${\displaystyle k={\frac {\omega }{c}}n}$ ve ${\displaystyle k_{1}={\frac {\omega }{c}}{n_{1}}}$ küre dışındaki ve içindeki dalga vektörünü ifade eder. Kürenin dışı ve içindeki kırılma indisleri ${\displaystyle n}$ ve ${\displaystyle n_{1}}$ ile gösterilir.

Sınır koşulları denklemlere uygulandıktan sonra Mie katsayıları elde edilir:

${\displaystyle c_{n}(\omega )={\frac {\mu _{1}\left[\rho h_{n}(\rho )\right]'j_{n}(\rho )-\mu _{1}\left[\rho j_{n}(\rho )\right]'h_{n}(\rho )}{\mu _{1}\left[\rho h_{n}(\rho )\right]'j_{n}(\rho _{1})-\mu \left[\rho _{1}j_{n}(\rho _{1})\right]'h_{n}(\rho )}}}$

${\displaystyle d_{n}(\omega )={\frac {\mu _{1}n_{1}n\left[\rho h_{n}(\rho )\right]'j_{n}(\rho )-\mu _{1}n_{1}n\left[\rho j_{n}(\rho )\right]'h_{n}(\rho )}{\mu n_{1}^{2}\left[\rho h_{n}(\rho )\right]'j_{n}(\rho _{1})-\mu _{1}n^{2}\left[\rho _{1}j_{n}(\rho _{1})\right]'h_{n}(\rho )}},}$

${\displaystyle b_{n}(\omega )={\frac {\mu _{1}\left[\rho j_{n}(\rho )\right]'j_{n}(\rho _{1})-\mu \left[\rho _{1}j_{n}(\rho _{1})\right]'j_{n}(\rho )}{\mu _{1}\left[\rho h_{n}(\rho )\right]'j_{n}(\rho _{1})-\mu \left[\rho _{1}j_{n}(\rho _{1})\right]'h_{n}(\rho )}}}$

${\displaystyle a_{n}(\omega )={\frac {\mu n_{1}^{2}\left[\rho j_{n}(\rho )\right]'j_{n}(\rho _{1})-\mu _{1}n^{2}\left[\rho _{1}j_{n}(\rho _{1})\right]'j_{n}(\rho )}{\mu n_{1}^{2}\left[\rho h_{n}(\rho )\right]'j_{n}(\rho _{1})-\mu _{1}n^{2}\left[\rho _{1}j_{n}(\rho _{1})\right]'h_{n}(\rho )}},}$

${\displaystyle \rho =ka}$

${\displaystyle \rho _{1}=k_{1}a}$

Bu katsayılarda ${\displaystyle a}$ kürenin yarıçapına, ${\displaystyle j_{n}}$ ile ${\displaystyle h_{n}}$ fonksiyonları da sırasıyla birince tip küresel Bessel ve Hankel fonksiyonlarına tekabül eder.

Mie saçılması nümerik olarak hesaplanırken sonsuz seri toplamının bir yerden sonra kesilmesi gerekir. Bununla ilgili en yaygın kriterlerden biri Wiscombe'un kriteridir ve ${\displaystyle L_{max}=x+4x^{1/3}+2}$ terimlerin doğruya yakın sonuçlar için yeterli olduğunu belirtir. Bu denklem de x, ${\displaystyle \rho }$ ile eştir.^[6]

Mie teorisinde ve saçılmada etkinlik katsayıları sıklıkla kullanılan parametrelerdendir. Bu katsayılar yok olma ${\displaystyle (Q_{e})}$, saçılma ${\displaystyle (Q_{s})}$ ve soğurma ${\displaystyle (Q_{a})}$ için tanımlanabilir.^[7][8] Bu katsayılar ilgili tesir kesitlerinin ışığın saçıldığı kürenin kesit alanına oranıdır. Örnek olarak, bir Mie saçılmasında saçılma etkinlik katsayısı ${\displaystyle Q_{s}={\frac {\sigma _{s}}{\pi a^{2}}}}$ formülü ile hesaplanabilir; bu denklemde ${\displaystyle \sigma _{s}}$ saçılma tesir kesiti ve a da parçacık yarıçapıdır.

Yok olma kesiti, Mie teorisinde şu şekilde tanımlanır:

${\displaystyle \sigma _{e}=\sigma _{s}+\sigma _{a}}$ and ${\displaystyle Q_{e}=Q_{s}+Q_{a}}$

Gene Mie teorisine göre, saçılma ve yok olma katsayıları sonsuz bir seri ile gösterilebilir:

${\displaystyle Q_{s}={\frac {2\pi }{k^{2}}}\sum _{n=1}^{\infty }(2n+1)(|a_{n}|^{2}+|b_{n}|^{2})}$

${\displaystyle Q_{e}={\frac {2\pi }{k^{2}}}\sum _{n=1}^{\infty }(2n+1)\Re (a_{n}+b_{n})}$

Mie teorisi, atmosfer biliminde bulut ve tozlardaki ışık saçılmasının incelenmesi için sıkça kullanılmaktadır. Teorinin diğer kullanım alanları arasında biyomedikal sistemler ile radarlar bulunmaktadır. Mie saçılımı aynı zamanda bazı metamateryal ve plazmonik yapıların teorisinde yer edinmiştir.^[4][9][10]

• Bohren, C. F.; Huffmann, D. R. (2010). Absorption and scattering of light by small particles (İngilizce). New York: Wiley-Interscience. ISBN 978-3-527-40664-7. 
• Jackson, John David (1998). Classical Electrodynamics (İngilizce). New York: Wiley. ISBN 9780471309321. 
• Maier, S. A. (2007). Plasmonics: Fundamentals and applications (İngilizce). New York: Springer. ISBN 9780387378251. 
• van de Hulst, H. C. (1957). Light scattering by small particles (İngilizce). New York: John Wiley and Sons. ISBN 9780486139753. 

• SCATTERLIB: Işık saçılması kodları koleksiyonu 26 Kasım 2020 tarihinde Wayback Machine sitesinde arşivlendi.
• Online Mie saçılması hesaplayıcısı 29 Ocak 2020 tarihinde Wayback Machine sitesinde arşivlendi.
• PyMieScatt 21 Ekim 2020 tarihinde Wayback Machine sitesinde arşivlendi., Mie saçılması Python kodu