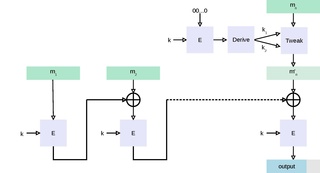
Merkle imza algoritması

Merkle imzası, anahtarlama ağaçları ve sayısal imza şemalarını birleştiren bir veri doğrulama yapısıdır. Özet değeri tabanlı kriptografidir ve Merkle ağacı da denen özet değeri ağacını kullanmaktadır. Verileri Lampart imza algoritması gibi tek kullanımlık şekilde imzalar. Ralph Merkle tarafından 1970 sonu itibarıyla geliştirilmiştir ve RSA, Dijital İmza Algoritması gibi geleneksel dijital imzalara alternatif olmuştur.

Merkle imza algoritmasının avantajı kuantum bilgisayarı algoritmalarına karşı dirençli olduğuna inanılıyor olmasıdır. Geleneksel açık anahtar algoritmaları olan RSA ve ElGamal gibi algoritmalar efektif kuantum bilgisayarlarının tasarlanabilir olmasıyla birlikte (Shor'un algoritmasına dayanarak) güvensiz hale geldi. Merkle imza algoritması sadece güvenilir bir özet değeri fonksiyonunun varlığına dayanmaktadır. Bu özelliği de Merkle imza algoritmasının çok esnek ve kuantum bilgisayarlarına dirençli olmasını sağlamaktadır. Merkle imzasının sonlu imza potansiyeli olan tek kullanımlık bir imza olduğu unutulmamalıdır; Moni Maor ve Moti Yung'un imza tabanlı tek yölü permütasyonlar üzerindeki çalışması ve fonksiyonlar (ve evrensel tek yönlü özet değeri fonskiyonunun icadı), Merkle benzeri imzaların tam bir imza algoritmasına dönüşmesine yol açmıştır.

Merkle imza algoritması tek açık anahtar olan pub ile sınırlı sayıda mesajın imzasında kullanılabilir. Muhtemel mesajların sayısı ikinin katı olmalıdır, dolayısıyla olası mesajların sayısını N = 2ⁿ ile gösterelim.

Ortak anahtar olan pub oluşturulması için ilk aşama N tane tek kullanımlık imza algoritmalarının (Lamport imza algoritması gibi) özel/açık anahtar çifti (X_i,Y_i) üretilmelidir. Her 1<= I <= 2ⁿ  için, ortak anahtarın özet değeri h_i = H(Y_i)  hesaplanır.

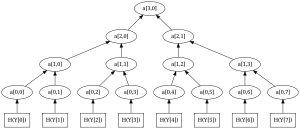
Bütün ${\displaystyle h_{i}}$${\displaystyle 2^{n}}$ yaprak özet değeri özyineli bir şekilde özet değerleri alınarak ikili ağaç formasyonunda Merkle ağacı oluşturulur.  ${\displaystyle a_{i,j}}$ ifadesinde yükseklik için ${\displaystyle i}$ ve sağ sol pozisyonu göstermek içinse ${\displaystyle j}$. Buna istinaden, ${\displaystyle h_{i}=a_{0,i}}$ özet değerleri yaprakları temsil etmektedir. Her iç düğümlerin değeri, kendi alt 2 çocuğunun değerlerinin birleşiminin özet değerlerinin alınması ile belirlenir. Örneğin, ${\displaystyle a_{1,0}=H(a_{0,0}||a_{0,1})}$ ve ${\displaystyle a_{2,0}=H(a_{1,0}||a_{1,1})}$. Bu şekilde, ${\displaystyle 2^{n}}$ yapraklı bir ağaçta ${\displaystyle 2^{n+1}-1}$ düğüm oluşturulmaktadır.

Merkle imza algoritmasının özel anahtarı bütün (X_i,Y_i) çiftleridir. Algoritmanın en büyük problemlerinden birisi bu özel anahtar kümesinin boyutunun mesaj sayısıyla doğrusal oranda büyüyor olmasıdır.

Açık anahtar pub ağacın kökü olan =a_n,0  değeridir. Tek açık anahtar Y_i 'nin genele açılması güvenliği kırmayacaktır. Ancak, bunların kullanımı genel için bir ihtiyaç değildir ve boyutlarını da küçültmek adına gizli tutmak mantıklı olacaktır.

Merkle imza algoritması ile M mesajını imzalamak için imzalayan bir (X_i,Y_i) anahtar çifti seçer, tek kullanımlık imza algoritması kullanarak imzalar ve ardından ek bilgileri ekleyerek aslında onun orijinal anahtar çiftlerinden biri olduğunu kanıtlar (bir sahtekar tarafından yeni yaratılanın yerine).

İlk olarak, imzalayıcı daha önce başka bir mesajı imzalamak için kullanılmamış (X_i,Y_i) çifti seçer ve tek kullanımlık imza algoritmasını mesajı imzalamak için kullanarak sig' imzasını ve karşılık gelen Yi açık anahtarını elde eder. Mesaj alıcısına (X_i,Y_i) çiftinin orijinal anahtar çiftlerinden biri olduğunu kanıtlamak için Merkle ağacının ara düğümlerini dahil ederek alıcının h_i=a_0,i değerinin ağacın kökünde bulunan an,o açık anahtarını hesaplamak için kullanıldığını doğrulamasını sağlar . a_0,i değerinden kök değerine giden yolda n+1 düğüm bulunur ve bunların her birini A0,...., An şeklinde ifade ederiz. A₀ = a_0,i = H(Y_i) yaprak değeri ve A_n = a_n,0 = pub ise kök değeri olmuş olur.

${\displaystyle A_{i}}$ düğümünün ${\displaystyle A_{i+1}}$.Alıcının önceki verilmiş olanla bir sonraki düğüm ${\displaystyle A_{i+1}}$ ${\displaystyle A_{i+1}}$.Bu düğüme ${\displaystyle {\text{auth}}_{i}}$, böylece ${\displaystyle A_{i+1}=H(A_{i}||{\text{auth}}_{i})}$. Bu sebeple,${\displaystyle {\text{auth}}_{0},\ldots ,{\text{auth}}_{n-1}}$${\displaystyle A_{n}=a_{n,0}={\text{pub}}}$${\displaystyle A_{0}=a_{0,i}}$ bir kimlik doğrulama yolu sağ taraftaki şekilde gösterilmektedir.

Bu düğümler auth₀,…,auth_n-1, Y_i ve tek kullanımlık imza olan sig' birlikte Merkle imza algoritması kullanarak bir M imzası oluştururlar:

sig = (sig' || Y_i || auth₀|| auth₁ ||…|| auth_n-1)

Ayrıca unutulmamalıdır ki Lamport imza algoritması imza için kullanılırken, sig' özel anahtar X_i'nin bir bölümünü içerir.

Alıcı açık anahtar pub, mesaj M ve imza sig = (sig' || Y_i || auth₀|| auth₁ ||…|| auth_n-1) bilmektedir.İlk olarak alıcı tek kullanımlık imza açık anahtarı Y_i kullanarak mesaja ait olan tek kullanımlık imza sig' doğrular. Eğer sig' M mesajına ait geçerli bir imza ise, alıcı tek kullanımlık imzanın açık anahtarının özet değerini alarak A₀ = H(Y_i) hesaplar.  j = 1,…, n-1  değerleri için, yol üzerindeki A_j düğümleri A_j = H(A_j-1 || auth_j-1) ile hesaplanır. Eğer A_n Merkle anahtar algoritmasına ait açık anahtar pub’a eşit ise  imza geçerlidir.

• G. Becker. "Merkle Signature Schemes, Merkle Trees and Their Cryptanalysis", seminar 'Post Quantum Cryptology' at the Ruhr-University Bochum, Germany.
• E. Dahmen, M. Dring, E. Klintsevich, J. Buchmann, L.C. Coronado Garca. "CMSS - an improved merkle signature scheme". Progress in Cryptology - Indocrypt 2006, 2006.
• E. Klintsevich, K. Okeya, C.Vuillaume, J. Buchmann, E.Dahmen. "Merkle signatures with virtually unlimited signature capacity". 5th International Conference on Applied Cryptography and Network Security - ACNS07, 2007.
• Ralph Merkle. "Secrecy, authentication and public key systems / A certified digital signature". Ph.D. dissertation, Dept. of Electrical Engineering, Stanford University, 1979. [1] 14 Ağustos 2018 tarihinde Wayback Machine sitesinde arşivlendi.
• Moni Naor, Moti Yung: Universal One-Way Hash Functions and their Cryptographic Applications .STOC 1989: 33-43
• S. Micali, M. Jakobsson, T. Leighton, M. Szydlo. "Fractal merkle tree representation and traversal". RSA-CT 03, 2003

• Efficient Use of Merkle Trees 17 Nisan 2017 tarihinde Wayback Machine sitesinde arşivlendi. -Merkle ağaçlarının asıl amacı olan birden fazla tek kullanımlık Lambort imzasının ele alınmasının RSA Labs tarafından açıklanması
• An introduction to hash-based signatures and Merkle signatures by Adam Langley. 14 Eylül 2018 tarihinde Wayback Machine sitesinde arşivlendi.
• A 4 parts series on hash-based signatures by David Wong. 5 Şubat 2018 tarihinde Wayback Machine sitesinde arşivlendi.