
Matematik ; sayılar, felsefe, uzay ve fizik gibi konularla ilgilenir. Matematikçiler ve filozoflar arasında matematiğin kesin kapsamı ve tanımı konusunda görüş ayrılığı vardır.
Sayı, sayma, ölçme ve etiketleme için kullanılan bir matematiksel nesnedir. En temel örnek, doğal sayılardır. Sayılar, sayı adı (numeral) ile dilde temsil edilebilir. Daha evrensel olarak, tekil sayılar rakam adı verilen sembollerle temsil edilebilir; örneğin, "5" beş sayısını temsil eden bir rakamdır. Yalnızca nispeten az sayıda sembolün ezberlenebilmesi nedeniyle, temel rakamlar genellikle bir rakam sisteminde organize edilir, bu da herhangi bir sayıyı temsil etmenin organize bir yoludur. En yaygın rakam sistemi Hint-Arap rakam sistemidir, bu sistem on temel sayısal sembol, yani rakam kullanılarak herhangi bir negatif olmayan tam sayının temsil edilmesine olanak tanır. Sayılar sayma ve ölçme dışında, etiketlerde, sıralamada ve kodlarda kullanılmak için de sıklıkla kullanılır. Yaygın kullanımda, bir rakam ile temsil ettiği sayı net bir şekilde ayrılmaz.

Aritmetik; matematiğin sayılar arasındaki ilişkiler ile sayıların problem çözmede kullanımı ile ilgilenen dalı. Aritmetik kavramı ile genellikle sayılar teorisi, ölçme ve hesaplama kastedilir. Bununla birlikte bazı matematikçiler daha karmaşık çeşitli işlemleri de aritmetik başlığı altında değerlendirirler.
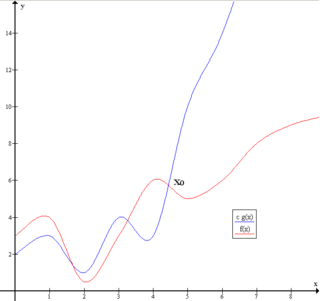
Büyük O (Big-Oh) gösterimi matematiksel bir gösterim olup işlevlerin (fonksiyonların) asimptotik davranışlarını tarif etmek için kullanılır. Bir işlevin büyümesinin asimptotik üst sınırını daha basit başka bir işlev cinsinden tanımlanması demektir. İki temel uygulama alanı vardır: matematik alanında genellikle kırpılmış bir sonsuz serinin kalan terimini karakterize etmek için kullanılır; bilgisayar bilimlerinde ise algoritmaların bilgi işlemsel karmaşıklığının çözümlemesi için kullanılır.

Braille alfabesi veya Körler alfabesi; 1821 yılında Louis Braille tarafından geliştirilmiş görme engelli insanların okuyup yazması için kullanılan bir alfabe yöntemidir. İki kolon taşıyan dikdörtgen düzen üzerine dizilmiş altı kabartılmış noktadan oluşur. Her iki kolonda üçer nokta bulunur. Noktalardan her biri 64 farklı kombinasyondan birini oluşturması için farklı şekillerde dizilir.
Artı işareti ve eksi işareti, matematiksel semboller olarak kullanılmakta olup, pozitif ve negatif fonksiyonların gösterilmesinde sırasıyla kullanılırlar. Bunun yanı sıra, + toplama işlemi için kullanılır ki bu işlem bir toplam sonucunu üretir, − ise çıkarma işlemi için kullanılır ve bir fark sonucunu meydana getirir. Bu işaretlerin kullanımı zamanla, daha az veya daha çok benzer diğer anlamlar kazanmıştır. Plus ve minus, Latincede sırasıyla "daha fazla" ve "daha az" anlamına gelmektedir.

Küme, matematikte farklı nesnelerin topluluğu veya yığını olarak tanımlanmaktadır. Bu tanımdaki "nesne" soyut ya da somut bir şeydir. Fakat her ne olursa olsun iyi tanımlanmış olan bir şeyi, bir eşyayı ifade etmektedir. Örneğin, "Tüm canlılar topluluğu", "Dilimiz alfabesindeki harflerin topluluğu", "Masamın üzerindeki tüm kâğıtlar" tümcelerindeki nesnelerin anlaşılabilir, belirgin oldukları, kısaca iyi tanımlı oldukları açıkça ifade edilmektedir. Dolayısıyla bu tümcelerin her biri bir kümeyi tarif etmektedir. O halde, matematikte "İyi tanımlı nesnelerin topluluğuna küme denir." biçiminde bir tanımlama yapılmaktadır.

Matematiksel yazılım; model, sayısal, sembolik veya geometrik veri analizi veya sayısal hesaplamalar için kullanılır. Matematiksel yazılımlar, başta eğitim olmak üzere bilim, sağlık, savunma, bilgisayar gibi alanlarda yeni şeyler üretme ve geliştirmede kullanılan programların genel adı. Matematik yazılımları kategorisinde; matematiksel gösterim, grafik oluşturma, çizim, modelleme, hesaplama, programlama ve benzeri türden programlar bulunur.
Bilgisayarlı cebir sistemi (BCS) sembolik matematiği kolaylaştıran yazılım programıdır. BCS işlevselliğinin özü sembolik biçimlerdeki matematiksel ifadelerin işleme koyabilmesidir.
Εpsilon, Yunan alfabesinin beşinci harfidir. Türkçedeki ince E sesi gibi okunur. Örnek: benim, esir vb.
Kuantum mekaniğine göre atomik orbital, elektronların atom çekirdeği etrafındaki konumunu ve dalga-benzeri özelliklerini tanımlayan bir matematiksel fonksiyondur. Elektronun atom çekirdeği etrafındaki belirli bir bölgede bulunma olasılığı bu fonksiyon aracılığı ile hesaplanabilir. Fizikte atomik, kimyada orbital olarak geçer.

Matematikte, tensör, çok boyutlu verinin simgelenebildiği geometrik bir nesnedir. Skaler denilen yönsüz nicel büyüklükler, vektör denilen yönlü büyüklükler ve matris denilen iki boyutlu nesneler birer tensördür. Tensör, tüm bu nesnelerin genelleştirilmiş halidir ve çok boyutlu veri kümeleri için kullanılır. Nesnenin kaç boyutla ifade edildiğine de tensörün derecesi denilir. Bir skalerin derecesi sıfır, bir vektörün bir, bir matrisin ise ikidir. Tensörler üç ve üzeri dereceye sahip olabilir.
Yunan harfleri; matematikte, bilimde ve mühendislikte ayrıca sabitler ve özel fonksiyonlar için sembollerle matematiksel notasyonun yapıldığı her yerde, özellikle belirli nicelikleri temsil eden değişkenler için kullanılır. Bu bağlamda, büyük ve küçük harfler farklı ve alakasız şeyleri simgelerler. Latin harfi biçimindeki Yunan harfleri genellikle kullanılmazlar: büyük A, B, E, H, I, K, M, N, O, P, T, X, Y, Z gibi. "i, o ve u" Latin harflerine yakından benzediklerinden, küçük ι (iota), ο (omikron) ve υ (ipsilon) nadiren kullanılır. Bazen Yunan harflerinin değişik fontları matematikte bambaşka semboller için kullanılır, özellikle de φ (fi) ve π (pi).

Minkowski diyagramı ya da uzay zaman diyagramı, 1908 yılında Hermann Minkowski tarafından geliştirilen ve uzay ve zaman, Özel görelilik teorisi içinde yer alan uzay ve zamanın, özelliklerinin örneklerini temin etmeyi sağlayan diyagram. Zaman genişlemesi ve uzunluk kısalması gibi fenomenlere ilişkin sayısal yönden bir kolay anlaşılabilme özelliği sağlıyordu ve bunu yaparken de matematiksel denklemleri kullanmıyordu.
Sembolik matematik; sembolik hesaplama ve cebirsel hesaplamadan oluşan bilgisayar cebrindeki, matematiksel ifadeleri ve diğer matematiksel nesneleri manipüle etmek için kullanılan algoritma ve yazılımların çalışması ve geliştirilmesine atıfta bulunan bilimsel bir alandır.Daha açıkça ifade etmek gerekirse, bilgisayar cebri bilimsel hesaplamanın bir alt alanı sayılır ve bununla beraber bilimsel hesaplama genelde yaklaşık kayan nokta sayılarına ve sayısal yaklaşımlara dayanmaktadır.Buna karşın sembolik hesaplama, hiçbir değişkeni içermeyen ifadelerle tam hesaplamayı vurgulamaktadır.Değişken içermeyen ifadelere ilişkin semboller manipüle edilmektedir ve adı bundan dolayı sembolik matematik olarak kabul edilir.

Matematik tarihi, öncelikle matematikteki keşiflerin kökenini araştıran ve daha az ölçüde ise matematiksel yöntemleri ve geçmişin notasyonunu araştıran bir bilimsel çalışma alanıdır. Modern çağdan ve dünya çapında bilginin yayılmasından önce, yeni matematiksel gelişmelerin yazılı örnekleri yalnızca birkaç yerde gün ışığına çıktı. MÖ 3000'den itibaren Mezopotamya eyaletleri Sümer, Akad, Asur, Eski Mısır ve Ebla ile birlikte vergilendirmede, ticarette, doğayı anlamada, astronomide ve zamanı kaydetmede/takvimleri formüle etmede aritmetik, cebir ve geometri kullanmaya başladı.
Matematik, sayı, uzay, matematiksel yapı ve değişim gibi konuları araştıran bir çalışma alanıdır. Matematik ve bilim arasındaki ilişki hakkında daha fazla bilgi Matematik ve bilim bölümünde bulunabilir.
Patrick du Val cebirsel geometri, diferansiyel geometri ve genel görelilik üzerine yaptığı çalışmalarla tanınan İngiliz bir matematikçi. Bir cebirsel yüzeyin Du Val tekilliği kavramı onun adını almıştır.
MacTutor Matematik Tarihi arşivi, John J. O'Connor ve Edmund F. Robertson tarafından sağlanan ve İskoçya'daki St Andrews Üniversitesi tarafından barındırılan bir web sitesidir. Birçok tarihsel ve çağdaş matematikçi hakkında ayrıntılı biyografilerin yanı sıra ünlü eğriler ve Matematik tarihindeki çeşitli konular hakkında bilgiler içerir.
Matematikte, Alman matematikçi David Hilbert tarafından 1920'lerin başında formüle edilen Hilbert'in programı, matematiğin temellerini açıklığa kavuşturmaya yönelik ilk girişimlerin tutarsız olduğu bulunduğunda, matematiğin temel krizine önerilen bir çözümdü. Çözüm olarak Hilbert, mevcut tüm teorileri sonlu, sonlu bir aksiyom dizisine dayandırmayı ve bu aksiyomların tutarlı olduğuna dair bir kanıt sunmayı önerdi. Hilbert, gerçek analiz gibi daha karmaşık sistemlerin tutarlılığının daha basit sistemleri kullanarak kanıtlayabileceğini gösterdi.Sonuçta matematiğin tamamının tutarlılığı temel aritmetiğe indirgenebilir.









