Işın izleme, gerçek dünyada ışığın ne şekilde hareket ettiğini göz önünde bulundurarak bir sahnenin görüntüsünü çizen bir grafik oluşturma yöntemidir. Ancak bu yöntemde işlemler gerçek yeryüzündeki yolun tersini izler. Gerçek dünyada ışık ışınları bir ışık kaynağından çıkar ve nesneleri aydınlatırlar. Işık, nesnelerden yansır ya da şeffaf nesnelerin içinden geçer. Yansıyan ışık gözümüze ya da kamera merceğine çarpar. Yansıyan ışık ışınlarının çoğu bir gözlemciye erişmediği için bir sahnedeki ışınları izlemek sonsuza dek sürebilir.
Doğru, matematikte mantıksal bir değerdir. Matematik'te ne olduğu belli olmayan (tanımsız) değerlerden biridir. Ayrıca geometride doğru ifadesi aynı doğrultuda olan ve her iki yönden de sonsuza kadar giden noktalar kümesi diye de tanımlanır. Bir doğru üzerinde en az 2 nokta, dışında da en az 1 nokta mevcuttur.
Doğrusal cebir ya da lineer cebir; matematiğin, vektörler (yöney), vektör uzayları, doğrusal dönüşümler, doğrusal denklem takımları ve matrisleri (dizey) inceleyen alanıdır. Vektör uzayları, modern matematiğin merkezinde yer alan bir konudur. Bundan dolayı doğrusal cebir hem soyut cebirde hem de fonksiyonel analizde sıkça kullanılır. Doğrusal cebir, analitik geometri ile de alakalı olup sosyal bilimlerde ve fen bilimlerinde yaygın bir uygulama alanına sahiptir.
Matematikte bir çizgi integrali, integrali alınan fonksiyonun bir eğri boyunca değerlendirildiği integraldir. Çeşitli farklı çizgi integralleri kullanılmaktadır. Kapalı eğrinin kullanıldığı durumlarda integrale kontür integrali denildiği de olmaktadır.
Sarmal, burgu şekilli, üç boyutlu bir şekildir. Sarmal şekilli gündelik nesnelere örnek olarak silindirik yay, vida ve minare merdiveni gösterilebilir. Sarmallar biyolojide de yer alır, DNA molekülü birbirine sarılmış iki sarmaldan oluşur, çoğu proteinde de alfa sarmal olarak adlandırılan sarmal yapılar bulunur. Sıfat hali için sarmal kullanılır.
Fresnel integrali, S(x) ve C(x), iki transendental fonksiyon'dur. Augustin-Jean Fresnel'e atfedilmiştir ve optikte kullanılmaktadır. Yakın alan Fresnel difraksiyon fenomeninde ortaya çıkar; aşağıdaki integral gösterimi ile tanımlanırlar:
Matematikte bir döşeme, aralarında boşluk bırakmadan veya örtüşmeden bir düzlemi kaplayan düzlemsel şekiller kümesidir. Bu kavram daha yüksek boyutlar için de genellenebilir, bu genişletilmiş anlamı için döşeme yerine tesselasyon terimi kullanılır. Tesselasyon M. C. Escher'in eserlerinde sıkça görülebilir. Tesselasyona sanat tarihi boyunca, antik mimariden modern sanata kadar rastlanabilir.
Geometride tetrahedron veya dört yüzlü, dört üçgen yüzden oluşan bir çokyüzlüdür (polihedron), her köşesinde üç üçgen birleşir. Düzgün dört yüzlü dört üçgenin eşkenar olduğu bir dört yüzlüdür ve Platonik cisimlerden biridir. Dörtyüzlü, dört yüzü olan tek konveks çokyüzlüdür. Tetrahedron isminin sıfat hali "tetrahedral"dır.
Hız, bir nesnenin hareket yönü ile birlikte olan süratini ifade eder. Hız, cisimlerin hareketini tanımlayan bir klasik mekanik dalı olan kinematikte temel bir kavramdır.
Matematikte Öklid uzayı, Öklid geometrisinin üç boyutlu uzayıdır ve bu kavramlar, çok boyutlu olarak genelleştirilir. “Öklid” terimi bu uzayları, Öklid geometrisi olmayan eğimli uzaydan ve Einstein'nın genel görelilik kuramından ayırt eder. Bu adı Yunan matematikçi Öklid'den dolayı almıştır.
Çifte doğrusallık, matematik'te, çiftdoğrusal işlemci her bir bağımsız dogrusal değişkenlerin üçüncü bir vektör uzayının bir öğesini elde etmek için iki vektör uzayı öğelerini birleştiren bir fonksiyonudur. Matris çarpimi bir örnektir.
Matematikte, Green kuramı basit, kapalı bir C eğrisi etrafındaki çizgi integrali ile C eğrisinin sınırlandırdığı D düzlem bölgesi üzerindeki çift katlı integral arasındaki ilişkiyi verir. Teorem adını matematikçi George Green'den almıştır ve daha genel hâli olan Stokes teoreminin iki boyuttaki özel durumudur.
Birim küre, belirli merkez noktasından 1 birim uzaklıkta olan noktalar kümesidir.Mesafelerin genellenmiş kavramları olarak da kullanılabilir.Kapalı bir birim küre, merkezden 1 birim az veya 1 birime eşit uzaklıktaki noktalar kümesidir.Genellikle, boşluktaki orijinden bir nokta ayırt edilmişitir ve bu noktanın birim kürenin veya birim topun merkezi olduğu anlaşılır.Bu yüzden birim küre ya da birim topun aynı olduğu söylenir. Örneğin;bir boyutlu küre, genellikle bir halka olarak adlandırılan bir yüzeydir ve çember bir içi yüzeye ve dış yüzeye sahipse iki boyutlu bir küredir.Benzer bir şekilde, halk dilinde küre olarak bilinen Öklid katısının yüzeyi iki boyutlu küredir ve ayrıca içi ve dış yüzeye sahip olduğunda üç boyutlu küre olur. Bir birim küre basitçe bir küre yarıçapına sahiptir.Birim kürenin önemi, herhangi bir kürenin ölçeklendirme ve çevirme kombinasyonlarına dönüşebilmesinden anlayabiliriz.Bu yolla, çalışırken kürenin temel özelliklerini daha aza indirgeyebiliriz.
Beş boyutlu uzay fikri, matematikte sıklıkla ortaya çıkan soyut bir terim.
Düzgün olmayan rasyonel temelli eğri, eğrileri ve yüzeyleri oluşturmak ve temsil etmek için bilgisayar grafiklerinde yaygın olarak kullanılan matematiksel bir modeldir. Hem analitik hem de modellenmiş şekilleri işlemek için büyük esneklik ve hassasiyet sunar. NURBS yaygın olarak bilgisayar destekli tasarım, imalat ve mühendislikte kullanılır ve IGES, STEP, ACIS ve PHIGS gibi çok sayıda endüstri çapında standardın parçasıdır. NURBS araçları ayrıca çeşitli 3B modelleme ve animasyon yazılım paketlerinde de bulunur. NURBS yüzeyleri, üç boyutlu uzayda bir yüzeye eşlenen iki parametrenin işlevleridir. Yüzeyin şekli kontrol noktaları ile belirlenir. NURBS yüzeyleri, kompakt bir biçimde basit geometrik şekilleri temsil edebilir. T-spline'lar ve alt bölme yüzeyleri, NURBS yüzeylerine kıyasla kontrol noktalarının sayısını iki kat azalttığı için karmaşık organik şekiller için daha uygundur. NURBS eğrilerini ve yüzeylerini düzenlemek oldukça sezgisel ve öngörülebilirdir. Kontrol noktaları her zaman doğrudan eğriye / yüzeye bağlanır veya bir lastik bantla bağlanmış gibi davranır. Kullanıcı arayüzünün türüne bağlı olarak, düzenleme, Bézier eğrileri için en açık ve yaygın olan bir elemanın kontrol noktaları aracılığıyla veya spline modelleme veya hiyerarşik düzenleme gibi daha yüksek seviyeli araçlar aracılığıyla gerçekleştirilebilir.
Adını Fransız matematikçi Jean Paul de Gua de Malves'den alan De Gua teoremi, Pisagor teoreminin üç boyutlu bir analojisidir.
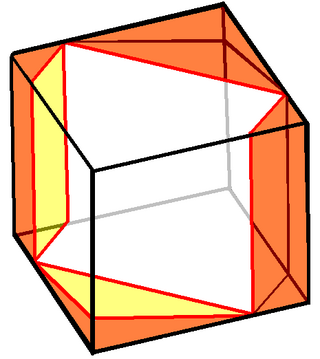
Prince Rupert'ın küpü, geometride, bir birim küp içine tüm boyunca kesilmiş bir delikten geçebilen en büyük küptür. Yani kenarları 1 birim uzunlukta olan bir küpten, küpü iki parçaya bölmeden geçebilir. Yan uzunluğu, içinden geçtiği birim küpünkinden yaklaşık %6 daha büyüktür. Tamamen bir birim küp içinde yer alan en büyük kareyi bulma sorunu ile çok yakından ilişkilidir ve aynı çözüme sahiptir.
Lineer cebirde, taban, bir vektör uzayını tanımlamak için yeterli vektör kümesidir. Bir V vektör uzayının alt kümesi B bu uzayın tabanıysa, V'nin tüm elemanları B'nin elemanlarının biricik sonlu doğrusal birleşimleri şeklinde yazılabilir. Bu doğrusal birleşimlerin katsayıları, vektörün B üzerindeki bileşenleri ya da koordinatları olarak adlandırılır. Taban B'nin elemanlarına taban vektörleri denir.
Dört boyutlu uzay (4B), üç boyutlu veya 3 boyutlu uzay kavramının matematiksel bir uzantısıdır. Üç boyutlu uzay, gündelik yaşamdaki nesnelerin boyutlarını veya konumlarını tanımlamak için yalnızca boyut adı verilen üç sayıya ihtiyaç duyulduğu gözleminin mümkün olan en basit soyutlamasıdır. Örneğin, dikdörtgen bir kutunun hacmi, uzunluğu, genişliği ve yüksekliği ölçülerek ve çarpılarak bulunur.
Sıradan trigonometri, 
Öklid düzlemi içindeki üçgenleri inceler. Gerçel sayılar üzerindeki sıradan Öklid geometrik trigonometrik fonksiyonları tanımlamanın birkaç yolu vardır, örneğin dik açılı üçgen tanımları, birim daire tanımları, seri tanımları, diferansiyel denklemler yoluyla tanımlar ve fonksiyonel denklemler kullanılarak tanımlar. Trigonometrik fonksiyonların genellemeleri, genellikle yukarıdaki yöntemlerden biriyle başlayıp Öklid geometrisinin gerçek sayıları dışındaki bir duruma uyarlanarak geliştirilir. Genel olarak trigonometri, her türlü geometri veya uzay içindeki nokta üçlülerinin incelenmesi olabilir. Bir üçgen en az sayıda köşeye sahip çokgendir, bu nedenle genelleştirmenin bir yönü açı ve çokgenlerin daha yüksek boyutlu analoglarını incelemektir: katı açılar ile tetrahedronlar ve n-simplices gibi politoplar.