
Matematikte türev, bir fonksiyonun tanımlı olduğu herhangi bir noktada değişim yönünü veya hızını veren temel bir kavramdır. Tek değişkenli bir fonksiyonun tanım kümesinin belli bir noktasında türevi, fonksiyonun grafiğine bu noktada karşılık gelen değerde çizilen teğet doğrunun eğimidir. Teğet doğru, tanım kümesinin bu noktasında fonksiyonun en iyi doğrusal yaklaşımıdır. Bu nedenle türev genellikle anlık değişim oranı ya da daha açık bir ifadeyle, bağımlı değişkendeki anlık değişimin bağımsız değişkendeki anlık değişime oranı olarak tanımlanır. Bir fonksiyonun türevini teorik olarak bulmaya türev alma denilir. Eğer bir fonksiyonun tanım kümesindeki her değerinde hesaplanan türev değerlerini veren başka bir fonksiyon varsa, bu fonksiyona eldeki fonksiyonun türevi denir.
Cebir sayılar teorisini, geometriyi ve analizi içine alan geniş bir matematik dalıdır. Temel matematik işlemlerinden, çember ve daire alanları bulmayı kapsayan geniş bir ilgi alanına sahiptir. Cebir, mühendislik ve eczacılık gibi birçok alanda kullanılmaktadır. Kuramsal cebir, ileri matematiğin bir dalı olmakla birlikte sadece uzmanlar tarafından çalışılan bir koldur.

İntegral veya tümlev, toplama işleminin sürekli bir aralıkta alınan hâlidir. Türev ile birlikte kalkülüsün temelini oluşturan iki işlemden birisidir. Kalkülüsün temel teoremi sayesinde aynı zamanda türevin ters işlemidir.

Matematikte, diferansiyel denklem, bir ya da birden fazla fonksiyonu ve bunların türevlerini ilişkilendiren denklemdir. Fizik, kimya, mühendislik, biyoloji ve ekonomi alanlarında matematiksel modeller genellikle diferansiyel denklemler kullanılarak ifade edilirler. Bu denklemlerde, fonksiyonlar genellikle fiziksel ya da finansal değerlere, fonksiyon türevleriyse değerlerin değişim hızlarına denk gelir.

Bifurkasyon (dallanma), ilk kez Henri Poincaré tarafından yaratılan bir kavramdır.

Matematikte logaritma, üstel işlevlerin tersi olan bir matematiksel fonksiyondur. Mesela, 1000'in 10 tabanına göre logaritması 3'tür çünkü 1000, 10'un 3. kuvvetidir,1000 = 10 × 10 × 10 = 103. Daha genel bir ifadeyle:

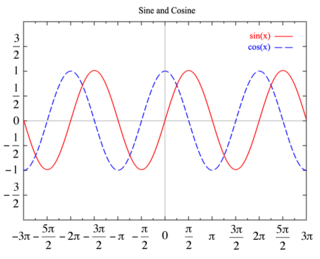
Sinüzoid dalga, matematikte, yalnız süreçlerde, dalgalı akım kuvvet mühendisliğinde ve diğer alanlarda sıklıkla bir fonksiyon olarak yer alır.
- Zamanın fonksiyon dalganlamasını (t) ile
- Merkezden doruk sapması = A
- açısal frekans
 (her saniyede radyanlar)
(her saniyede radyanlar) - başlangıç evresi (t = 0) = θ
- θ değişen evrelerle ilgilidir. Başlangıç evresi sıfırsız olduğu zaman yekpare dalga biçiminin görünümü parça θ/ω saniyeler tarafından zamanda değişir. Bir negatif değer gecikmeyi ve pozitif değer avantajı gösterir.
Matematikte sonuşmaz veya asimptot, belirli bir A eğrisine istenildiği kadar yaklaşabilen ikinci bir B eğrisine verilen addır. Bir başka deyişle, A üzerinde ilerledikçe, A ve B arasındaki mesafe azalır ve sıfıra yaklaşır. Asimptot kelimesi, Yunanca "beraber düşmek" anlamındaki simpiptein fiilinin olumsuz halinden türemiştir.

Matematik bilim dalında bir bozulmuş dağılım desteği sadece tek bir noktadan oluşan bir ayrık rassal değişken için bir olasılık dağılımıdır. Bu rassal değişken için örnekler her iki tarafı da yazı olan özel bir madeni disk veya her altı yüzü de aynı sayıyı gösteren özel bir zar olabilir. Örneklerden de görülebildiği gibi, bu türlü rassal değişken günlük yaşantıya göre hiç rastgelelik niteliği taşımamaktadır; ancak matematik bilimi içinde bulunan rassal değişken tanımlama özelliklerinin hepsini tatmin etmektedir.

François Viete Fransız matematikçi. Adıyla anılan Vieta formüllerini keşfetmiştir.

Pareto dağılımı, olasılık kuramı ve istatistik bilim dallarında birçok pratik uygulaması bulunan ve "küçük" bir nesnenin bir "büyük" nesneye dağılımında kararlılık elde edildiği hallerde kullanılan bir sürekli olasılık dağılımı veya bir güç kuramıdır. İlk olarak bir İtalyan iktisatçısı olan Vilfredo Pareto tarafından ekonomilerde bireylerin servet dağılımını göstermek için kullanılmıştır. İktisat bilim dalı dışında bu dağılım Bradford dağılımı adı altında da bilinmektedir.

Karmaşık analiz ya da başka bir deyişle kompleks analiz, bir karmaşık değişkenli fonksiyonları araştıran bir matematik dalıdır. Bir değişkenli karmaşık analize ya da çok değişkenli karmaşık analizle beraber tümüne karmaşık değişkenli fonksiyonlar teorisi de denilir.

Sayısal analiz, diğer adıyla nümerik analiz veya sayısal çözümleme, matematiksel analiz problemlerinin yaklaşık çözümlerinde kullanılan algoritmaları inceler. Bu nedenle birçok mühendislik dalı ve doğa bilimlerinde önem arz eden sayısal analiz, bilimsel hesaplama bilimi olarak da kabul edilebilir. Bilgisayarın işlem kapasitesinin artması ile gündelik hayatta ortaya çıkan birçok sistemin matematiksel modellenmesi mümkün olmuş ve sayısal analiz algoritmaları burada ön plana çıkmıştır. 21. yüzyıldan itibaren bilimsel hesaplama yöntemleri mühendislik ve doğa bilimleri ile sınırlı kalmamış ve sosyal bilimler ile işletme gibi alanları da etkilemiştir. Sayısal analizin alt başlıklarına adi diferansiyel denklemlerin yaklaşık çözümleri ve özellikle veri biliminde önem taşıyan sayısal lineer cebir ile optimizasyon örnek gösterilebilir.

Matematikte, Fourier serileri bir periyodik fonksiyonu basit dalgalı fonksiyonların toplamına çevirir.
Paramanyetik bir malzemede, malzemenin mıknatıslanması genel olarak uygulanan manyetik alanla orantılıdır. Fakat eğer malzeme ısıtılırsa, bu oran düşer: Belirli bir sıcaklığa kadar, mıknatıslanma sıcaklıkla ters orantılıdır. Bu kavram “Curie Yasası” tarafından kapsanmaktadır:


Parametre belirli bir sistemi tanımlamak veya sınıflandırmak için yardımcı olabilecek herhangi bir özellik. Parametre, sistemi tanımlarken veya performansını, durumunu değerlendirirken yararlı veya kritik olan bir sistem unsurudur.
Floquet teorisi, periyodik katsayılı doğrusal diferansiyel denklem sistemlerinin çözümü ile ilgilenen bir matematik alt dalıdır. Floquet teorisi,

Popülasyon ekolojisi, tür popülasyonlarının dinamikleri ve bu popülasyonların çevre ile nasıl etkileşime girdiği ile ilgilenen ekolojinin bir alt alanıdır. Gruplar halinde birlikte yaşayan türlerin popülasyon büyüklüklerinin zaman ve mekan içinde nasıl değiştiğinin incelenmesidir ve ekolojinin matematiksel olarak incelenen ve modellenen ilk yönlerinden biridir.

Rekabet, temini sınırlı olan kaynağa ihtiyaç duyan canlıların veya türlerin arasında yaşanan bir etkileşimdir. Rekabet, her iki organizmanın da uyum başarısını düşürür çünkü canlılardan birinin varlığı her zaman diğerine düşen kaynak miktarını azaltır.





















