Kuantum mekaniğine giriş
Kuantum mekaniği madde ve atomların ve atom içindeki parçacıklar ölçeğinde enerji ile etkileşimlerinin davranışını açıklayan bilimsel ilkeler organıdır: Bu makaleye teknik olmayan konuların tanıtımında ulaşabilirsiniz.
Klasik fizik astronomik cisimlerin davranışları dahil madde ve gözle görülebilir seviyedeki enerjiyi insan deneyleri için tanıdık ölçekte açıklamıştır. Bu modern bilimin ve teknolojinin çoğunluğu için anahtar rolü oynar. Ayrıca 19. Yüzyılın sonlarına doğru, bilim uzmanları klasik fiziğin açıklayamadığı büyük (makro) görüntüleri ve küçük (mikro) dünyaları keşfettiler. Bu sınırlamalar ile yüzleşen fizik iki büyük devrime yol açtı: görelilik kuramı ve kuantum mekaniği. Bu makale fizikçilerin klasik fiziğin sınırlarını nasıl keşfettiğini ve 20. yüzyılın ilk yıllarında kuantum kuramının temel kavramlarının nasıl geliştiğini açıklar. Bu kavramlar yaklaşık olarak keşfedildikleri sırayla anlatılmıştır.
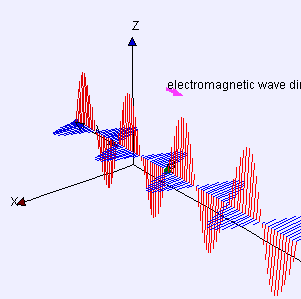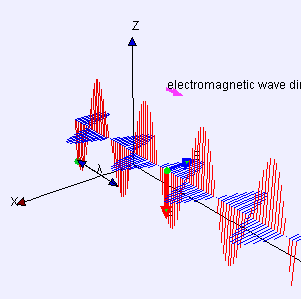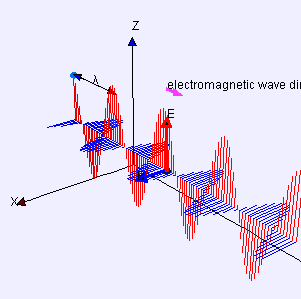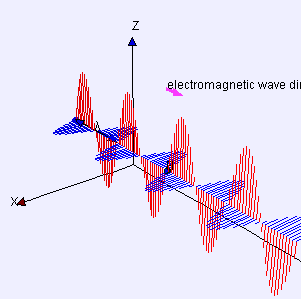
Kuantum mekaniğinin bazı yönleri, sezgiler açısından paradoksal görünebilir çünkü bunlar klasik fiziğin mükemmel bir yakınlaşması olduğunu ve büyük uzunluk ölçeklerinde görülenden oldukça farklı davranış tanımladığını gösterir. Örneğin ışık enerji paketleri halinde gelir. Bu enerji paketleri foton olarak isimlendirilir ve kuantum mekaniğinde bazen parçacık bazen de dalga özelliği gösteren bir hem parçacık hem de dalga olarak tanımlanır. Kuantum mekaniği enerjileri, renkleri ve elektromanyetik radyasyonun tüm biçimlerinin spektral yoğunluklarını tahmin eder.
Kuantum mekaniğinin belirsizlik ilkesi bir parçacığın hem konumunun hem de momentumunun aynı anda belirli bir hassasiyetten daha hassas bir şekilde ölçümlenemeyeceğini belirtir. Bu durum klasik fizik için söz konusu olmayan bir özelliktir.
Birinci kuantum teorisi: Max Planck ve siyah cisim ışınımı

Bir nesnenin sıcaklığı nedeniyle nesnenin yüzeyinden yayılan elektromanyetik termal radyasyondur. Eğer cisim yeterli miktarda ısıtılırsa spektrumun kırmızı ucunda ışık yaymaya başlarlar. red hot. Isıtma daha kısa dalga boylarında (yüksek frekansların) ışığın renklerinin maviden beyaza, beyazdan sarıya, sarıdan kırmızıya değişmesine neden olur. Bunun mükemmel bir verici ve mükemmel bir soğurucu olduğu ortaya çıktı. Mükemmel siyah duran nesneler soğuk olduğu zaman cisim bütün ışığı emdiği için bunun üzerine düşer ve hiçbirini yaymaz. Sonuç olarak, ideal termal yayıcılar siyah cisim olarak bilinir ve radyasyon emdiği için siyah cisim radyasyonu denir.
19 yüzyılın sonlarında termal radyasyon oldukça deneysel olarak iyi karakterize olmuştur.[note 1] Ayrıca klasik fizik sıcaklık ve radyasyonun baskın frekansı arasındaki ilişkiyi açıklayamamıştır. Hatta klasik fizik kısa dalga boylarında sıcak cisimlerin enerjiyi sonsuz hızla yaydığı kabul edilir. Açıkça yanlış olan bu sonuç morötesi felaket olarak bilinir. Fizikçiler çalışma yaptıkları tek bir teori için deneyler sonucu elde ettikleri sonucu açıklamışlardır.

Her osilatörün herhangi bir enerjiyi istediği miktarda yaymanın mümkün olmasını beklemekten çok, tek karakteristik bir frekansta enerji birimlerini bir tam sayı sayı ürettiğini varsaymak zorunda olduğumuzu deneysel sonucu anlayabiliriz. Diğer bir deyişle, her bir osilatör enerji nicelemiş oldu. " Planck'a göre her osilatör için enerji kuantum, osilatör frekansına orantılıdır ve orantılılık sabiti artık Planck sabiti olarak da bilinir.
Planck kanunu fizikteki ilk kuantum teorisidir ve Planck enerji miktarındaki keşfiyle Fizikte büyük ilerlemelere yol açtığı için 1918 yılında Nobel Ödülü'nü kazandı.[2] Ayrıca aynı zamanda Planck'ın görünüm nicelemesi tamamen matematiksel bir numara yerine, (biz artık inanıyoruz gibi) dünya anlayışımızda köklü bir değişim oldu.[3]
Fotonlar: ışığın kantizasyonu

1905'te Albert Einstein daha fazla yol kat etti. Albert Einstein kantizasyonun sadece matematiksel bir hile olmadığını önerdi: bir ışık demeti enerjisi fotons.[4] Tek bir fotonun enerjisi Planck'ın sabit ile çarpılma sıklığı ile elde edilir:
Yüzyıllar boyunca, bilim adamları ışığın iki olası teorileri arasında tartıştılar: bu dalga mı yoksa ufak parçacıkların akması mı? 19. yüzyıla gelindiğinde, bu tür kırılma, yansıma ve polarizasyon gibi gözlenen etkileri açıklamak mümkün olduğu için tartışmalar genellikle dalga teorisinin lehine yerleşmiş olduğu kabul edilmiştir. James CLERK Maxwell elektriğin, manyetiğin ve ışığın aynı olayın bütün tezahürleri olduğunu gösterir: elektromanyetik alan. Klasik elektromanyetik kurallarının toplam kurulumu olarak bilinen Maxwell denklemleri ışığı dalga olarak tanımlar: Titreşen elektrik ve manyetik alanların birleşimidir. Dalga teorisi lehine kanıt üstünlüğünü yüzünden, başlangıçta Einstein'ın fikirleri büyük şüpheyle karşılandı. Sonunda, ancak, foton modeli favori oldu; kendi lehine olan en önemli kanıtlarından biri aşağıdaki bölümde açıklanan fotoelektrik etki ve birkaç şaşırtıcı özelliklerini açıklamak. Bununla birlikte, örneğin kırınım gibi ışık diğer özelliklerini anlamaya yardımcı olmak için dalga benzetmesi vazgeçilmez olmuştur.
Fotoelektrik etki

1887 yılında Heinrich Hertz ışığın metalden elektron yayabildiğini gözlemlemiştir.[5] 1902 tarihinde Philipp Lenard elektronun yayabildiği maksimum enerjinin ışığın frekansıyla ilişkili olduğunu ama yoğunluğuyla bağlantısı olmadığını bulmuştur; eğer frekans çok düşük olursa, herhangi bir elektron yoğunluk bağımsız olarak dışarı atılır. Elektronun yayılmasına neden olan düşük frekanslı eşik frekansı olarak adlandırılan ışık her metal için farklıdır. Bu gözlem elektronun enerji radyasyon yoğunluğu ile orantılı olması gerektiğini öngörür klasik elektromanyetizma ile çelişmektedir.[6] :24
Einstein ışık huzmesi parçacıklarının (fotonlar) bir akım olduğunu ve ışın frekansı f ise daha sonra her foton hf eşit bir enerjiye sahip olduğunu olduğunu varsayarak etkisini açıkladı.[5] Elektron sadece tek fotonların vurdu olması muhtemeldir ve en çok enerjiyi hf elektronu verir.[5] Bu nedenle huzmesinin yoğunluğunun bir etkisi yoktur {{# tag: ref | Aslında orada yoğunluk bağımlı etkileri olabilir, ancak non-lazer kaynakları ile ulaşılabilir yoğunluklarda bu etkiler gözlemlenemez edebilirsiniz | grup = not}.} sadece frekans elektron kazandırdığı edilebilir maksimum enerji belirler.[5]
Eşik seviyesi etkilerini açıklamak için, Einstein bu metalden bir elektron çıkarmak için, φ ile gösterilen iş fonksiyonlu adı verilen enerjiden belirli bir miktar alındığını savunur.[5] Her bir metal için farklı bir enerji vardır. Fotonun enerji çalışma fonksiyonu daha az ise, o zaman metalden elektron çıkarmak için yeterli enerji taşımaz. Eşik frekansı,f0, enerji çalışma işlevine eşit olan bir foton sıklığıdır:
Eğer f, f0 dan büyük olursa, hf enerjisi elektron çıkarmak için yeterli olur. Dışarı elektronlar en fazla foton enerjisinin eksi metalden elektron çıkarmak için gerekli olan enerjiye eşit bir kinetik enerjisine EKsahiptir:
Einstein'ın ışık açıklaması parçacıklardan oluşan varlık olarak nicelenmiş ve enerji Planck'ın kavramı genişletilmiştir: belirli bir frekans olan f tek bir foton enerjisi hf değişmeyen miktarda sunar. Başka bir deyişle bireysel atomlar enerjiyi az ya da çok teslim edebilir ancak onların frekansına bağlıdır. Foton bir parçacık olmakla birlikte, yine de frekans dalga benzeri özelliğine sahip olarak tarif edilir. Bir kez daha, ışığın parçacık hesabı "tehlike" ediliyordu.[7] {{# tag: ref | Einstein'ın fotoelektrik etki denklemi' elde edilecek ve "foton" kavramını gerek kalmadan' açıklanabilir. Bu elektromanyetik radyasyon sürece malzemede elektronlar kuantum mekaniğinin yasaları tarafından tedavi edilir. Sonuçlar, termal ışık kaynakları için sayısal olarak doğru hem elektron emisyon oranı yanı sıra açısal dağılımı için (güneş, ampuller, vs.) Grup = not | Bu noktada daha fazla bilgi için, NTRS.NASA.gov 2 Temmuz 2013 tarihinde Wayback Machine sitesinde arşivlendi.</ref>|group=note}}
Belirli bir dereceye kadar enerji içeren ışığın sonuçları
Elektromanyetik radyasyon ile her bir fotonun enerjisi arasındaki ilişki kızılötesi ışıkların güneş yanığına neden olmadığını gösterirken morötesi ışıkların güneş yanığına neden olduğunu gösterebilir. Morötesi ışık fotonu büyük miktarda enerji iletebilir- yeterli miktarda hücre hasarı güneş yanığı meydana getirebilir. Kızılötesi ışık fotonu düşük miktarda enerji iletebilir-sadece kişilerin cildinin ısınmasını sağlar. Yani bir kızılötesi lamba kimseye bir güneş yanığı veremez belki soğuk bir odada yeterince büyük yüzeye sahip olduğunda insanları sıcak ve rahat tutmaya yardımcı olur.
Eğer her bir foton eşit enerjiye sahip olsaydı, bir "yüksek enerji" fotonu konuşmak doğru olmazdı. Taşan yüzeylerle birlikte saniyede gelen daha fazla fotonlar yüzünden yüksek frekanslı ışıklar daha fazla enerji taşır. Düşük frekanslı ışık yalnızca aynı nedenle daha fazla enerji taşıyabilir. Eğer bütün fotonların aynı enerjiyi taşıdığı doğru olsaydı fotonların teslim oranını iki katına çıktığında, o zaman, her saniye gelen enerji birimlerinin sayısını iki katına çıkar. Einstein bağımsız dalgaların klasik parçacık bazlı analizlerin lehindeki yaklaşımı ayrı adımlardaki frekanslarla değişebileceği yaklaşımını reddeder. Aynı frekansa sahip tüm fotonlar aynı enerjiye sahiptir ve farklı frekansların tüm fotonlarla orantılı farklı enerjilere sahiptir.
Doğada tek fotonlar nadir olarak olarak rastlanır. Güneş fotonları sürekli olarak fotonları elektromanyetik sıklıklarda emer bu yüzden bunlar sürekli bir dalga olarak değil, ayrı ayrı birimler olarak yaymak için görünür. 19. yüzyılda Hertz ve Lennard mevcut sürüm kaynaklarının paylaşıldığı karakteristiktelerdir. Kırmızı parıltılı demirden ya da kırmızı ışık yayan yıldız güzel enerji içerdiği söylenebilir. Bazı radyasyonların vücudumuza sürekli eklenerek devam eden toplam enerjinin kırmızı, turuncu, yeşil, sarı, mavi, mor ve bunun gibi ışıklar yaydığı tahmin edilmiştir. Büyük yıldız ve demir büyük parçalar olarak daha sonra mutlaka yelpazenin mor sonuna doğru daha fazla renk ile kızdırma olurdu ama öyle değil. Işıma gövdesinin rengini değiştirmek için sıcaklığı değiştirmek gerekir. Sıcaklığındaki bir artış daha yüksek frekanslarda foton yaymasını sağlar ve daha yüksek düzeyde tek tek atomuna uyarmak için kullanılabilir ve kuantum enerjisi değiştir.
Bir yıldız (ya da demir bir parça) ile birim zaman başına toplam yayılan enerji, hem zaman birimi başına fotonların sayısı, hem de dâhil olan bir foton her biri tarafından taşınan enerji miktarına bağlıdır. Diğer bir deyişle, bir ışıma gövdesinin karakteristik frekansı kendi sıcaklığına bağlıdır. Fizikçiler sadece bireysel ve neredeyse ayırt edilemez fotonların büyük sayılar içeren ışık demetlerini aradığı zaman, tek tek foton enerji düzeylerinin önemini anlamak zor olacaktı. Bu yüzden fizikçiler fotoelektrik etkileri gösteren cihazı bulduklarında, başlangıçta yüksek ışık yoğunluğunun fotoelektrik bir cihazdan daha yüksek bir voltaj üretmesi beklenmektedir. Bu spektrumun kırmızı sonuna doğru güçlü ışık ışınları hiç elektrik potansiyeli üretmeyeceği bulunurken, spektrumunun menekşe ucuna doğru ışık ışınları yüksek ve daha yüksek voltajlar üretebileceğini keşfedildi. Einstein'ın fikri farklı enerji içeren her bir birimlerin onların frekansına bağlı olmasıdır ve bu fikir şimdiye kadar mümkün oldukça garip görünürken deney sonuçları sonucu açıklaması yapılmıştır.
Enerji fotonun verilen herhangi bir frekanstaki sabit niceliğini açığa vurmasına rağmen önceki bölgedeki ışık emilim karşısında bir fotoelektrik cihazındaki elektronların enerjisi ilk durumda düzgün değildir. Anormal sonuçlar bireysel elektronların olması durumunda oluşur. Örneğin; karaktersizliği düşük frekanslı aydınlatma emildiğinde fotoelektrik cihaz elektron atılırken uyarılır. İstatiksel yönden Bir fotoelektrik cihazın karakteristik davranışları denge seviyesindeyken o elektronların büyük çoğunluğunun davranışını yansıtır. Bu nokta kuantum dinamikleri bireysel parçacıkların çalışması ile klasik fizik olarak kümelendiği parçacıkların çalışması arasındaki ayrımı kavramada yararlıdır.
Maddenin kantizasyon: Bohr atom modeli
20. yüzyılın şafağında tarafından, küçük yoğunluğun çevresinde pozitif yüklü çekirdeği çevreleyen negatif yüklü elektronların bir yaygın bulut ile atom modeli oluşturması gereklidir. Bu özellikler güneşin etrafındaki gezegenler gibi çekirdeğin etrafında elektronların çember şeklinde yörünge oluşturan bir model önerdi.Klasik teoride yörüngedeki elektronlara göre merkezcil ivmeyi gören ve bu nedenle ikinci bir kısmını onunla çarpışıp elektromanyetik radyasyon oluşturmasına göre bu atom modelinin sabit olmadığı bilinir.
İkinci ilişki bulmaca atomlu sürüm spektrumu olmasıyla ilişkilidir. Bir gaz ısıtıldığında, sadece kesikli frekanslarda ışık yayar. Resimde gösterildiği gibi, örneğin, hidrojen ile dışarı verilen görünür ışık, dört farklı renk oluşur. Buna karşılık, beyaz ışık görülebilir frekansların bütün aralığı boyunca kesintisiz bir sürümü oluşur. On dokuzuncu yüzyılın sonunda, farklı çizgilerin frekanslarının neden olduğunu açıklayan bu basit kural ya da yoğunlukları hakkında herhangi bir tahmin yapmamasına rağmen birbirleriyle nasıl ilişkili olduğunu göstermiştir. Formül aynı zamanda gözlemlenemeyen morötesi ve kızılötesi ışıkların bazı ek spektral çizgilerini tahmin etmiştir. Bu çizgiler daha sonra deneysel olarak gözlemlenmiş ve formüle olan güven artmıştır.

1885 yılında İsviçreli matematikçi Johann Balmer her dalga boyu λ keşfetti, hidrojenin görünür spektrumda (lambda) bazı tam sayı {{matematik ile ilgili | n} } aşağıdaki denklemle verilmiştir
B sabittir ve Balmer 364.56 nm eşit olduğuna karar vermiştir.
1888 yılında Johannes Rydberg büyük ölçüde yaygın ve Balmer formülü açıklayıcı yarar arttı. n iki tam sayılar ile ilgili | O { λ} {math} öngördü ve m şimdi olarak bilinen ne göre, Rydberg formülü:[8]
R Rydberg sabiti, 0,0110 nm -1 eşit ve n m daha yüksek olmalıdır.
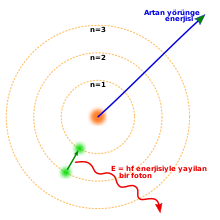
1913 yılında Niels Bohr kuantumlanan elektron yörüngelerine sahip yeni bir atom modeli önerdi: elektronlar gezegenlerin güneş etrafında yörünge olarak hala çok çekirdeğini yörünge, ancak sadece herhangi bir mesafede yörüngeye değil, belli yörüngelerde yaşaması için izin verilmektedir.[9] Bir atom enerjiyi yaydığı (veya emdiği) zaman tahmin edilebileceği gibi, elektron, başka çekirdeğin etrafındaki bir yörüngede sürekli olarak hareket etmez. Elektron bir yörüngeden diğerine atlamak yerine bir foton şeklinde ışık yayar. Fotonların her element tarafından yayılan olası enerjisi farklı yörüngeler arasındaki enerji farkı olarak belirlenmiştir ve bu her element için olan yayınlama spektrumu birçok hat içerir.[10]

Bohr modelinde elektron basit olarak enerjinin sürekli olarak yayılmasına ve çekirdeğin içinde çarpıştırılmasına izin vermez. Yörüngenin yakınlaşmasına izin verildiği zaman sonsuza kadar kararlı olur. Bohr modeli yörüngenin bu yolla nicelemesini açıklayamadı ve aynı zamanda birden fazla elektron atomlar için doğru tahminler yapamadı ya da bazı spektral çizgilerinin diğerlerinden neden daha parlak olduğunu açıklayamadı. Bohr modeli için bazı temel varsayımların yanlış bulunmasına rağmen yayımlanma spektrumundaki ayrı çizgiler atomların bazı elektron özelliklerinin doğru olduğunu nitelendirmiştir. Elektronların asıl davranışı çarpıcı şekilde Bohr atomundan ve bizim gördüğümüz ve her günkü deneyimlerimizden farklıdır; atomun modern kuantum mekaniğinin modeli aşağıda tartışılmıştır.
belirli dereceye kadar enerji içeren elektronlar Bohr L kavramlaştırılmış:
- ,
- .
Dalga-parçacık ikiliği

Tıpkı ışık gibi hem dalga hem de parçacık hareketi ve benzeri özelliklere sahiptir. Broglie hipotezi de ayrıca dalga hareketi özelliklerene sahiptir.[11]
Maddenin elektron dalgası olarak davranmasını ilk defa deneysel olarak elektronlar için gösterilmiştir: Elektron demeti sadece bir ışık demeti ya da bir su dalgası gibi, kırınım sergileyebilir. Benzer bir dalga gibi. Benzer dalga olayları daha sonra atomlar ve hatta küçük moleküller için gösterildi. Bir nesne ile ilişkili dalga boyu, λ, Planck sabiti h aracılığıyla momentum, p ile ilgilidir:[12][13] Dalga-parçacık ikiliği kuantum fiziğinde tamamlayıcılık ilkesinin bir örneğidir. Dalga-parçacık ikiliğinin zarif bir örneği olan çift yarık deneyi aşağıdaki bölümde ele alınmaktadır.
Çift-yarık deneyi

Orijinal olarak 1827 yılında Thomas Young ve Augustin Fresnel tarafından gerçekleştirilen çift-yarık deneyinde, bir ışık demetinin bir ekranda açık ve koyu bantlarla bir girişim deseni üreten, iki dar, yakın aralıklı yarıktan yönlendirilir. Yarıklardan biri örtbas edilirse, saf parazit nedeniyle saçakların yoğunluğu her yerde yarıya olacağını bekleyebilirsiniz. Aslında çok daha basit bir model olan basit kırılma modeli görülmektedir. Kapalı bir yarık daha basit çaplı ve açık yarığa zıt bir desene neden olur. Tam olarak su dalgaları ile aynı davranışı gösterdiği ortaya konabilir ve böylece çift-yarık deneyi ışığın dalga doğasının bir gösterisi olarak görülür.
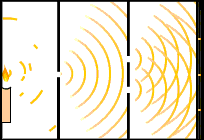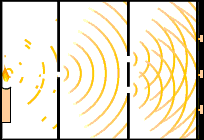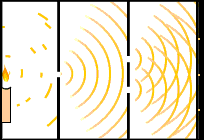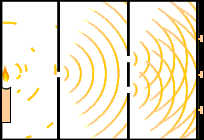
Çift yarık deneyi elektronları, atomları ve hatta molekülleri kullanılarak gerçekleştirilmiştir ve aynı zamanda parazit desenin aynı tipi olarak görülmüştür. Bu nedenle, tüm madde parçacıklarının ve dalga karakterlerinin bütün özelliklere sahip olduğu ortaya çıkartılmıştır
Kaynak yoğunluğunun bir seferde cihaz boyunca geçen tek bir parçacığın (örneğin, foton veya elektron) aşağı açılmasına rağmen, aynı girişim deseni zaman içinde gelişir. Bu tespit edildiğinde kuantum parçacığı çift yarıktan geçen ancak parçacık olan bir dalga gibi davranır. Bu kuantum tamamlayıcılığının tipik bir özelliğidir: kuantum parçacığı parçacık gibi özellikleri ölçmek için dalga gibi davranır.Detektör ekranında herhangi bireysel parçacığın ortaya çıkılı tamamen rastgele bir yöntemin sonucudur.
Bohr modeline Uygulama
De Broglie Bohr modelini geliştirerek bir çekirdeğin etrafındaki yörüngede bir elektronun dalga gibi özelliklere sahip olabileceğini gösterdi. Özellikle, bir elektron, sadece çekirdek çevresinde bir dalga izin durumlarda gözlenecektir. Durağan bir dalganın örneği iki ucundan sabitlenmiş ve titreşim yaratabilen bir viyolin yayıdır. Telli bir çalgı aleti tarafından oluşturulan dalgalar salınım yaparak aşağı yukarı hareket ettiği görülür. Ayakta duran dalga boyu titreşimli nesnenin boyu ve sınır koşullarıyla ilgilidir. Örneğin, viyolan yayı iki ucundan sabitlendiği için, dalga boyu 2l/n (l uzunluk ve n bir pozitif tam sayı) olan durağan bir dalga taşıyabilir.
De Broglie izin verilen elektron yörüngelerinin çevresindeki yörünge dalga boylarının bir tam sayı olacağını önerdi. Elektronun dalga boyu çekirdekten belirli uzaklıklarda sadece Bohr yörüngelerinde mümkün olduğunu belirler. Buna karşılık olarak, belirli bir değerden daha küçük çekirdeğin yörünge kurması imkânsızdır. Çekirdekten minimum olası mesafeye Bohr yarıçapı denir. p. 87</ref> De Broglie kuantum teorik olayları tedavisi Schrödinger başlangıç noktası olarak hizmet ettiğinde o dalga denklemini kuantum teori olayına göre oluşturulmuştur.
Modern kuantum mekaniğinin gelişimi
Bohr gençlik sınıf arkadaşlarını hidrojen sürüm spektrumunun yoğunluğunu bulmak ve açıklamak için tayin ettiğinde, Werner Heisenberg daha basit problemleri açıklayarak güncel bir başarı yakaladı. 1925 yılında, matematiksel benzetme vasıtasıyla, o yoğunluklarının klasik hesaplanması için kuantum mekanik analoğunu yazdı.[14][15] Kısa bir süre sonra, Heisenberg'sin meslektaşı Max Born farklı enerji seviyeleri arasındaki geçişleri için olasılıkları hesaplamada Heisenberg yönteminin en iyi matematiksel matris kavramının kullanabileceğini fark etti.[note 2]
Schrödinger eşitliği olarak adlandırılan matematiksel model kuantum mekaniğinin çekirdeğini oluşturur. Bu model kuantum sisteminin izin verilen sabit durumunu tanımlar ve zamanla fiziksel kuantum durumunun fiziksel sisteminin nasıl değiştiğini tanımlar.[16] O matematiksel modelin sonunda denilen yapılmış Schrödinger denklemi onun yaratıcısı oldu sonra, kuantum mekaniğine merkezi, tanımlayıp bir kuantum sisteminin durağan durumlarını açıkladı ve nasıl zaman fiziksel kuantum durumlarının bir sistem değişiklikleri oluğunu gösterdi.[17] Dalga bir "dalga fonksiyonu" olarak bilinen bir matematiksel fonksiyonu olarak tarif edilmektedir ve genellikle Yunan harfi ("psi") ile temsil edilir. Schrödinger'in kedisini tanıttığı yazıda, o dalga fonksiyonu "ölçüm sonuçlarının olasılığını öngörmek için bir araç" sağlar ve "ölçüm beklentilerinin olası gelecek sonuçlarını" sağlar. Schrödinger denklemine bakınız. Schrödinger proton tarafından oluşturulan elektrik potansiyelin bir kuyu içinde protonlar tarafından oluşturularak hareket eden klasik dalgaların hidrojen enerji seviyelerini hesaplamayı mümkün kılmıştır Bu hesaplama Bohr modelinin enerji seviyelerini doğru olarak çoğaltamaz. Schrödinger Heisenberg'in matris mekaniğini ve onun kendi dalga mekaniğinin elektron davranışları ve özellikleri ile ilgili aynı tahminleri yaptığını kanıtlamıştır; matematiksel olarak iki teori aynıdır fakat bu iki adam ortak teori yorumu yapmada anlaşamamıştır. Örneğin Heisenberg teorik tahminlerine göre elektronların atom içindeki yörüngeler arasında ani geçişlerde bir problem görmemiştir (as paraphrased by Wilhelm Wien[18]) ama Schrödinger bu teorinin sürekli dalga hareketi özelliklerinin kuantum hakkında saçmalık denmemesini(Wilhelm Wien tarafında) ummuştur.
Kopenhag yorumu

Heisenberg ve diğerleri bu deneysel sonuçlarının ne olduğunu ve matematiksel modellerin asıl anlamının ne olduğunu açıklamaya çalıştılar. Kuantum mekaniğinin Copenhagen yorumları olarak bilinen bu açıklamalar kuantum mekaniğinin ölçümlerini inceleyen ve açıklayan gerçekçilik doğasının ve kuantum mekaniğinin matematiksel formülleriyle ve ölçümleriyle açıklamayı hedeflemiştir.
Kopenhag yorumunun temel ilkeleri şunlardır:
- Sistem tamamen bir dalga fonksiyon tarafından tarif edilmektedir.
- Schrödinger denklemleri tarafından zamanla nasıl değişir.
- Doğanın tasvirleri temel olasılıklarıdır. Bir olayın olasılığı - örneğin, bir parçacık, ekranda iki yarık deneyi gösterilir - Onun dalga fonksiyonunun büyüklüğünün mutlak değerinin karesi ile ilişkilidir. (Kopenhag yorumu nedeniyle dalga fonksiyonunu Max Born için fiziksel bir anlam verir, kural tarihi: olasılık genliği).
- Sistemin aynı zamanda bütün özelliklerinin değerlerini bilmek mümkün değildir; bu özellikler olasılıklar tarafından tanımlanan doğruluk olarak bilinmez.(Heisenberg'in belirsizlik ilkesi).
- Enerji gibi olan madde dalgaları sergiler-ikilik dalga parçacıkları. Deney maddenin parça hareketinin özelliklerini gösterir; ama ikisini aynı zamanda gösteremez. (Bohr nedeniyle tamamlayıcılık ilkesi).
- Ölçüm cihazları aslında klasik cihazlardır ve konum ve momentum gibi klasik özellikleri ölçmek için kullanılır.
- Büyük sistemlerin kuantum mekanik tanımı klasik tanıma yaklaşık olmalıdır. (Bohr ve Heisenberg'in Yazışmalar ilkesi)
Bu ilkelerin çeşitli sonuçları aşağıdaki alt bölümlerde daha ayrıntılı olarak tartışılmıştır.
Belirsizlik ilkesi

kazandı.[19]]]
Örneğin bir araba bir radar hız tuzağı geçiyor - biz bir nesnenin konumunu ve hızını ölçmek istediğinizi varsayalım. Biz arabanın zaman içinde belli bir anda kesin bir konuma ve hıza sahip olduğunu varsayalım, bizim ölçümlerimizin bu değerleri ölçüm donanım kalitesine bağlı olduğunu nasıl doğrudur- eğer ölçüm donanımın kesinliğini artırırsak doğru değerlere yakın sonuçlar elde ederiz. Özellikle karşı yönün ve pozisyonun etkilemediği arabanın hızını tam olarak nasıl ölçtüğümüzü varsayarız. 1927 yılında Heisenberg bu varsayımların doğru olmadığını kanıtlamıştır. Kuantum mekaniği fiziksel özelliklerinin belirli çiftleri, konum ve hız gibi, her ikisi de isteğe bağlı hassas bilinmezlik göstermektedir.[20] Daha çok kesin olarak bilinen özellik diğerlerinden daha az kesinlik gösterir. Bu durum bilinmezlik ilkesi olarak bilinir. Belirsizlik ilkesi, bizim ölçüm cihazlarının doğruluğu hakkında bir açıklama değildir ama sistemin kendisi doğası hakkındadır-arabanın kesin bir konum ve hıza sahip olduğu varsayımımız yanlış olmuştur. Araba ve insanların bir ölçekte, bu belirsizlikler önemsenmeyecek kadar çok küçük, ama atomları ve elektronları ile uğraşırken bu belirsizlikler önemli hale gelir. Heisenberg'in verdiği bir örneğe göre bir ışık fotonu kullanarak bir elektronun konum ve momentum ölçümü hesaplanmıştır. Düşük frekanslı bir fotonun rahatsızlığı ile - yani belirsizliği ile-. Momentumu daha az olur ama pozisyonunun ölçüm etkisi daha güvenilir olur.
Belirsizlik ilkesi bir parçacığın konum ve momentumun belirsizlik ürününün (momentumun kütle ile çarpılan hızıdır) asla belirli bir değerden daha az olamadığını ve bu değerin Planck sabiti ile ilgili olduğunu matematiksel olarak gösterir.[21]
Dalga etkisinin çöküşü
Dalga fonksiyon çöküşü ne olursa olsun bu bir açıklama sıkıntısıyken kesin bir durumda sistemin tarifi ile sistemin kararsız halinin açıklamasını değiştirmek daha rahat hale gelir. Doğanın oluşma durumlarının açıklamaları tartışmalıdır. Fotonun bir algılama ekranında gösterilmeden önce herhangi bir zamanda olasılıkların gösterimi sadece bir dizi ile tarif edilebilir. Eğer kamera, zaman ve cihaz etkileşim alanı CCD'nin nerede etkileşim yaptığı gösterildiği zaman cihazın çok dar limitlerde olduğu bilinir. Ancak, foton kaybolduğunda ve dalga fonksiyonunda onunla kaybolur. Bunun yerine tespit ekranında bazı fiziksel değişim, örneğin, fotoğraf filmi, bir tabaka içinde bir açık nokta ya da bir CCD gibi bir hücrede elektrik potansiyel değişikliği ortaya çıkmıştır.
Özdurumlar ve özdeğerleri
Belirsizlik ilkesi yüzünden pozisyon ve parçacıkların momentumları hakkındaki tablolar sadece pozisyon veya momentumun bazı sayısal değere sahip olacağı bir olasılık kararlaştırabilir. Bu nedenle açıkça böyle bir olasılık bulutu içinde kesin bir değere sahip bir durumdaki elektron ile belirsiz olan durum arasındaki farkı formüle etmek gerekmektedir. Nesne bazı durumlarda sıkıştırılırken bir öz durumuna sahip olduğu söylenir.
Pauli dışlama kuralı

1924 yılında, Wolfgang Pauli gözlenen moleküler spektrumları ve kuantum mekaniğinin tahminleri arasındaki tutarsızlıkları iki olası değerler ile birlikte göstererek yeni kuantum derecesini (ya da kuantum numarası) önerdi. . Özellikle atomik hidrojenin spektrumu bir ikili ya da sadece bir satır beklenen küçük bir miktar ile farklı çift hatları vardı. Pauli kendisinin atomların aynı kuantum sayısı dâhilinde bulunan atomların var olamayacağını söyleyen dışlama ilkesini formüle etmiştir. "[22]
Bir yıl sonra Unlenbeck ve Goudsmit Pauli’nin dönme denilen bir özellik ile özgürlüğün yeni derecesini tespit ettiler. Ralph Kronig kökenli fikir elektronların eksende dönme hareketi yapmasıdır. Dönme kayıp manyetik momentleri hesaplayabilir ve aynı yörüngede olan iki elektronun farklı yönlerde dönen uzak kuantum durumlarını işgal etmelerine izin verir. Böylece dışlama ilkesi tatmin edici bir hal alır. Kuantum sayısı dönme(pozitif veya negatif) duygusunu temsil eder.
Hidrojen atomu için uygulamalar
Atomunun Bohr modeli nükleer güneşin etrafındaki elektronlarla birlikteki esas bir gezegenidir. Ancak, belirsizlik ilkesi bir elektronun aynı anda bir gezegen ile yaptığı şekilde tam yerini ve hızını belirtemez. Klasik yörüngelerin yerine elektronlar yerleşik atomik yörünge olarak bilinir. Bir yörüngenin elektron bulundurabileceği olası yerleri "bulutlardır daha doğrusu kesin bir konumdan daha olası bir dağılımıdır.[22] Her bir yörünge iki boyutludan ziyade üç boyutludur ve %95 elektron olan bu bölge üç boyutlu bölgesi olarak tasvir edilir.[23]
Schrödinger iyi bir elektrik potansiyeliV, "dalga fonksiyonu" Ψ ile temsil edilen bir dalga gibi bir hidrojen atomu elektron gibi muamele edilmesiyle hidrojen enerji seviyelerini hesaplamak mümkün olduğunu, V, proton tarafından oluşturularak gösterilmiştir. Schrödinger'in denkleminin çözümleri elektron konumlarındaki ve yerlerindeki olasılıklar dağıtımları içindir. Yörüngeler üç boyutta farklı şekillere sahiptir. Farklı yörüngelerin farklı enerjileri hesaplanabilir ve Bohr modelinin enerji seviyeleri doğru şekilde eşleştirilebilir.
Schrödinger’in resmi dâhilinde her bir elektron dört özelliğe sahiptir:
- Bir "yörünge" tanımı parçacığın daha az enerjili çekirdeğe daha yakın ya da fazla enerjili çekirdekten daha uzak olup olmadığını gösterir;
- Yörüngelerin "şekli" küresel veya diğer türlü;
- Yörüngenin "eğimi", manyetik momentini belirleyen z-ekseni etrafında belirlenir.
- Elektronun "dönüşü"
Bu özelliklerin toplu adı elektronun kuantum durumudur. Kuantum durumu her bir özellikte verilen numaralar tarafından tanımlanabilir; bunlar elektronun kuantum numaraları olarak bilinir. Elektronun kuantum durumu dalga denklemi tarafından tanımlanmıştır. Pauli dışlama ilkesi, bir atomun içinde herhangi iki elektronun dört sayıların aynı değerlere sahip olabileceğini söyler.

Yörüngeyi açıklayan ilk özellik temel kuantum numarasıdır, n, n Bohr modelindekiyle aynıdır. n her bir yörüngenin enerji seviyesini belirtir. Bu olası n değerleri tam sayıdır.
l ile belirtilen diğer kuantum sayısı olan azimuthal yörüngenin şekli olarak tanımlanır. Şekli yörüngenin açısal momentumunun sonucudur. Açısal momentumu hızlandırmak veya dış kuvvet etkisi altında yavaşlatmak için kullanılan eğirme nesnesinin direncini temsil eder. Azimutal kuantum sayısı, çekirdeğin etrafında bir elektronun yörünge açısal momentumu temsil eder. l için olası değerler 0 ile n − 1 arasındaki tam sayılardır:
Her yörünge şeklinin kendi harfi vardır. İlk şekli s (anımsatıcı varlık "küre") ile gösterilir. Bir sonraki şekil p harfi ile gösterilmiştir ve bir dambıl bir formu vardır. Diğer yörüngeler daha karmaşık şekillere sahiptir (atomik yörünge bakın) ve harfler d, f ve g ile gösterilir.
Üçüncü kuantum sayısı, manyetik kuantum sayısı, elektronun manyetik an tarif eder ve ml (ya da m) ile gösterilir. ml için olası değerler −l ile l arasındaki tam sayılardır
Manyetik kuantum sayısı belirli bir yönde açısal momentum bileşeni ölçer. Keyfi yönü geleneksel olarak z-yönünde seçilir.
Dördüncü kuantum sayısı, (elektronun dönmesi "yönlendirme" ile ilgilidir) Spin kuantum sayısı +1⁄2 veya −1⁄2 değerleridir ve ms ile gösterilir.
Dirac dalga denklemi

Paul Dirac 1928 yılında Pauli denklemini genişletmiştir. Bu denklem elektronların dönmesini tanımlayarak özel görelilik hesaplanmıştır. En basit elektromanyetik etkileşim kullanarak Dirac elektronun dönme ile ilişkili olan manyetik moment değerini tahmin etmek mümkündür ve klasik fizik tarafından yönetilen dönen yüklü bir küre olamayacak kadar büyük olduğu deneysel olarak gözlemlenerek bir değer bulundu. O hidrojen atomunun spektral hatları için çözdü ve Sommerfeld'in ilk prensibi başarılı bir Hidrojen spektrumunun ince yapısı için bir formül üretmeyi başardı.
Dirac'ın denklemlerinin önerdiği yeni çözümler enerji için negatif değerler vermiştir. Bu çok parçacıklı kuantum alan teorisine neden olmuştur.
Kuantum dolaşıklığı

Pauli çıkarma ilkesi bir sistemdeki iki elektronun aynı durumda bulunamayacağını söyler. Doğa açık olasılıklardan ayrılır ancak bu iki elektron iki durumlarda birbiri üzerine ‘bindirilmiş’ olabilir. Hiçbir şey, üst üste dalga "çöküşü" kadar kesin değildir ve o anda bir elektron o yerde üst üste bindirilmiş iki dalga karmaşık değerli genliklerinin toplamının mutlak değerinin karesi olarak olasılık gösterir. Bu durum çok soyuttur. Aşağıdaki gibi iki zıt durumlarda aynı olan ve her biri üzerine bindirilmiş olduğu zaman ortaya çıkan dolaşmış fotonları düşünmenin somut bir yoludur.
Kuantum mekaniğinin tamamlanmamış bir teori olduğunu göstermeye çalışan Einstein eski çeşitli özellikleri ölçtüğünde iki ya da daha fazla parçacığın eskiden birbirleriyle etkileşim içinde olduğunu söyleyen tahminlerinin kuvvetli bir şekilde bağ kurduğunu gösterdi. Einstein etkileşimleri açıklamak için klasik yollar aradı.
Şimdi EPR çelişkisi olarak bilinen tartışma Einstein, Podolsky ve Rosen(1935; kısaltılmış EPR) gibi ünlü raporlarda başarılı bir şekilde çözümlenmiştir. Kopenhag yorumuna göre ise şimdi genellikle yerel gerçekçilik denen, EPR, bir parçacığın aynı zamanda konuma ve momentum sahip olduğunu kuantum teorisinde göstermeye çalışırken tek bu iki özelliğin aslında sadece tek bir anda var olduğunda ölçülebileceğini söyler. EPR sonucuna göre kuantum teorisinin tamamlanmamış olduğunu doğanın fiziksel özelliklerini dikkate alarak reddetmiştir. (Einstein, Podolsky ve Rosen 1935 şu anda fizik dergilerinde Einstein'ın en çok yayınlanan yayınıdır.) Aynı yıl, Erwin Schrödinger kelime "dolanması" kullanmış ve beyan etmiştir. Karmaşıklığın gerçek bir durum olup olmadığı sorusu hala anlaşmazlık içindedir. Bell eşitsizlikleri Einstein'ın iddialarına en güçlü meydan okumadır.
Kuantum alan teorisi

Paul Dirac'ın elektromanyetik alanları nitelendirmeye başlamasıyla birlikte Kuantum alan teorisi 1920'lerden sonra başlamıştır.
Fizikteki bir alanın (örneğin manyetizma gibi) uzayda ve bölgede belirli bir etkisi vardır (örneğin magnetizma) varlığı."[24] Alan gibi gösterilen diğer etkileri yerçekimi ve statik elektrik.[25] In 2008, fizikçi Richard Hammond yazmıştır.
Bazen kuantum alan teorisini (QFT) ve kuantum mekaniğini(QM) ayırt ederiz. Parçacıkların sayısını belirten kuantum mekaniği sabittir ve elektromanyetik gibi alanlar klasik varlıklardır. Kuantum alan teorisi başka bir adıma atlamış ve parçacıkların oluşturulmasına ve imha edilmesine izin verilmiştir. . . .
Ayrıca o kuantum mekaniğine eklenmiştir ve kuantum mekaniğine genellikle başvurmak için kullanılır. "[26]:108
1931 yılında, Dirac daha sonra anti-madde olarak bilinen parçacıkların varlığını önerdi. anti-matter.[27] Dirac 1933 yılında atom teorisinin yeni üretken biçimlerini keşfetmek için Schrödinger Nobel Fizik Ödülü'nü paylaştı.[28]
Kuantum elektrodinamiği[
Elektromanyetik kuvvetin kuantum teorisinin ismi kuantum elektrodinamik (QED). Kuantum elektrodinamiği anlama elektromanyetizma ile başlar. Elektromanyetizma elektrodinamik olarak adlandırılabilir çünkü bu elektrik ve manyetik kuvvetler arasındaki dinamik etkileşimlerdir. Elektromanyetizma elektrik yük ile başlar.
Elektrik yükler elektrik alanın kaynağı ve yaratıcısıdır. Elektrik alan elektrik yük taşıyan parçacıkların üzerine uygulanan kuvvetin alanıdır. Bu elektron proton ve diğerlerin arasındaki her bir taneciği içerir. Kuvvet olarak uygulanan elektrik kuvvetin hareketi, akımın akışı ve manyetik alan üretilmiştir. Manyetik alan da elektrik akıma neden olur(hareket eden elektronlar). Elektrik ve manyetik alanın etkileşimine elektromanyetizma denir.Yüklenmiş parçacıkların, elektrik akımların, elektrik alanların ve manyetik alan etkileşimlerinin fiziksel tasvirlerine elektromanyetizma denir.
Paul Dirac 1928 yılında elektromanyetizmanın relativistik kuantum teorisini üretti. Bu modern kuantum elektro-dinamiğinin öncülerinden olmasıyla bu modern teorinin temel maddelerine sahip oldu. Ayrıca çözülemeyen sonsuzluklar sorunu bu göreli kuantum teorisi ile geliştirdi. Yıllar sonra yeniden normalleştirme ile bu sorun çözüldü. Başlangıçta onun yaratıcılarından bazıları tarafından bir şüpheli gözükse de geçici izlek olarak izlendi, yeniden normalleştirme sonunda QED fiziğin diğer alanlarında önemli bir hal aldı ve kendi içinde tutarlı bir araç olarak benimsenmiştir. Ayrıca,1940'larda Feynman diyagramları, belirli bir olaya ilişkin tüm olası etkileşimleri tasvir etmiştir. Diyagramlar elektromanyetik kuvveti etkileşen parçacıklar arasındaki fotonlar olduğunu gösterdi.
Deneysel olarak doğrulanmış olan kuantum elektrodinamik bir tahmini örneği kuzu değiştirmesidir. Bu seslendirmeler sayesinde elektromanyetik alanın kuantum doğası otomda enerji seviyelerine ya da iyonların biraz sapmasına neden olacağını gösterir. Sonuç olarak, spektral çizgiler değişebilir veya bölünebilir.
1960'larda fizikçiler QED son derece yüksek enerjilerde bozulduğunu fark etti. Bu tutarsızlıklardan itibaren parçacık fiziğinin Standart Model teorisinde yüksek enerjili arızaların giderildiği keşfedildi. Standart Model teorisi elektro-manyetiği ve zayıf etkileşimleri birleştirir. Bu elektro-zayıf teorisi denir.
Yorumlama
Fiziksel ölçümler, denklemler ve kuantum mekaniği ilgili öngörüleri tutarlı ve onay için çok yüksek bir düzeyde tuttu. Ancak, bu soyut modeller gerçek dünyanın yatan doğası hakkında soruları sorduklarında rakip cevaplar aldı
Uygulamalar
Kuantum mekaniği lazer, transistor, elektron mikroskopu ve manyetik direnç uygulamaları içerir. Kuantum mekanik uygulamaları özel bir sınıf gibi süper akışkan helyum ve süper iletkenler gibi Makroskopik kuantum olaylarıyla ilgilidir. Yarıiletkenlerin çalışması modern elektronik için vazgeçilmez olan diyot ve transistorun icadına yol açtı.[29]
Ayrıca bakınız
|
|
Notlar
- ^ Radyasyon sıcaklığı ile güçlü bir değişiklik olduğu ne dalga boyu Wien değiştirme kanunu ile verilir, ne de birim alan başına yayılan genel güç Stefan-Boltzmann kanunu ile verilir.
- ^ Erwin Schrödinger'in de Broglie hipotezi dayandırıldığı 1925 yılında öğrenildi ve 1926 ilk yarısında başarılı olarak kuantum mekanik dalga davranışını tanımlamıştır.
Kaynakça
- Bernstein, Jeremy (2005). "Max Born and the quantum theory". American Journal of Physics. 73 (11). s. 999. Bibcode:2005AmJPh..73..999B. doi:10.1119/1.2060717.
- Beller, Mara (2001). Quantum Dialogue: The Making of a Revolution. University of Chicago Press.
- Bohr, Niels (1958). Atomic Physics and Human Knowledge. John Wiley & Sons]. ASIN B00005VGVF. ISBN 0-486-47928-5. OCLC 530611.
- de Broglie, Louis (1953). The Revolution in Physics. Noonday Press. LCCN 53010401.
- Einstein, Albert (1934). Essays in Science. Philosophical Library. ISBN 0-486-47011-3. LCCN 55003947.
- Feigl, Herbert; Brodbeck, May (1953). Readings in the Philosophy of Science. Appleton-Century-Crofts. ISBN 0-390-30488-3. LCCN 53006438.
- Feynman, Richard P. (1949). "Space-Time Approach to Quantum Electrodynamics" (PDF). Physical Review. 76 (6). ss. 769-789. Bibcode:1949PhRv...76..769F. doi:10.1103/PhysRev.76.769.[]
- Feynman, Richard P. (1990). QED, The Strange Theory of Light and Matter. Penguin Books. ISBN 978-0-14-012505-4.
- Fowler, Michael (1999). The Bohr Atom. University of Virginia.
- Heisenberg, Werner (1958). Physics and Philosophy. Harper and Brothers. ISBN 0-06-130549-9. LCCN 99010404.
- Lakshmibala, S. (2004). "Heisenberg, Matrix Mechanics and the Uncertainty Principle". Resonance, Journal of Science Education. 9 (8).
- Liboff, Richard L. (1992). Introductory Quantum Mechanics (2.2yayıncı= bas.).
- Lindsay, Robert Bruce; Margenau, Henry (1957). Foundations of Physics. Dover. ISBN 0-918024-18-8. LCCN 57014416.
- McEvoy, J. P.; Zarate, Oscar (1996). Introducing Quantum Theory. ISBN 1-874166-37-4.
- Nave, Carl Rod (2005). "Quantum Physics". HyperPhysics. Georgia State University. 17 Temmuz 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 11 Haziran 2014.
- Peat, F. David (2002). From Certainty to Uncertainty: The Story of Science and Ideas in the Twenty-First Century. Joseph Henry Press.
- Reichenbach, Hans (1944). Philosophic Foundations of Quantum Mechanics. University of California Press. ISBN 0-486-40459-5. LCCN a44004471.
- Schlipp, Paul Arthur (1949). Albert Einstein: Philosopher-Scientist. Tudor Publishing Company. LCCN 50005340.
- Scientific American Reader, 1953.
- Sears, Francis Weston (1949). Optics (3.3yayıncı=Addison-Wesley bas.). ISBN 0-19-504601-3. LCCN 51001018.
- Shimony, A. (1983). "(title not given in citation)". Foundations of Quantum Mechanics in the Light of New Technology (S. Kamefuchi et al., eds.). Tokyo: Japan Physical Society. s. 225.; cited in: Popescu, Sandu (1996). "Action and Passion at a Distance: An Essay in Honor of Professor Abner Shimony - yardımcı yazar =Daniel Rohrlich". arXiv:quant-ph/9605004 $2.
- Tavel, Morton (2002). Contemporary physics and the limits of knowledge. Rutgers University Press. ISBN 978-0-8135-3077-2.
- Van Vleck, J. H.,1928, "The Correspondence Principle in the Statistical Interpretation of Quantum Mechanics", Proc. Nat. Acad. Sci. 14: 179.
- Wheeler, John Archibald; Feynman, Richard P. (1949). "Classical Electrodynamics in Terms of Direct Interparticle Action". Reviews of Modern Physics. 21 (3). ss. 425-433. Bibcode:1949RvMP...21..425W. doi:10.1103/RevModPhys.21.425.
- Wieman, Carl; Perkins, Katherine (2005). "Transforming Physics Education". Physics Today. 58 (11). s. 36. Bibcode:2005PhT....58k..36W. doi:10.1063/1.2155756.
- Westmoreland; Benjamin Schumacher (1998). "Quantum Entanglement and the Nonexistence of Superluminal Signals". arXiv:quant-ph/9801014 $2.
- Bronner, Patrick; Strunz, Andreas; Silberhorn, Christine; Meyn, Jan-Peter (2009). "Demonstrating quantum random with single photons". European Journal of Physics. 30 (5). ss. 1189-1200. Bibcode:2009EJPh...30.1189B. doi:10.1088/0143-0807/30/5/026.
- ^ Francis Weston Sears (1958). Mechanics, Wave Motion, and Heat. Addison-Wesley. s. 537.
- ^ "The Nobel Prize in Physics 1918". Nobel Foundation. 5 Eylül 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 1 Ağustos 2009.
- ^ Kragh, Helge (1 Aralık 2000). "Max Planck: the reluctant revolutionary". PhysicsWorld.com. 1 Nisan 2012 tarihinde kaynağından arşivlendi. Erişim tarihi: 11 Haziran 2014.
- ^ Einstein, Albert (1905). "Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt" (PDF). Annalen der Physik. 17 (6). ss. 132-148. Bibcode:1905AnP...322..132E. doi:10.1002/andp.19053220607. 22 Ağustos 2014 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 11 Haziran 2014., translated into English as On a Heuristic Viewpoint Concerning the Production and Transformation of Light 11 Haziran 2009 tarihinde Wayback Machine sitesinde arşivlendi.. The term "photon" was introduced in 1926.
- ^ a b c d e Taylor, J. R.; Zafiratos, C. D.; Dubson, M. A. (2004). Modern Physics for Scientists and Engineers. Prentice Hall. ss. 127-9. ISBN 0-13-589789-0.
- ^ Stephen Hawking, kısacası evren, Bantam, 2001.
- ^ Dicke ve Wittke,Kuantum Mekaniğine Giriş, s. 12
- ^ Taylor, J. R.; Zafiratos, C. D.; Dubson, M. A. (2004). Modern Physics for Scientists and Engineers. Prentice Hall. ss. 147-8. ISBN 0-13-589789-0.
- ^ McEvoy, J. P.; Zarate, O. (2004). Introducing Quantum Theory. Totem \Books. ss. 70-89, especially p. 89. ISBN 1-84046-577-8.
- ^ Dicke and Wittke, İntroduction to Quantum Mechanics, p. 10f.
- ^ J. P. McEvoy and Oscar Zarate (2004). Introducing Quantum Theory. Totem Books. s. 110f. ISBN 1-84046-577-8.
- ^ Aczel, Amir D., Entanglement, p. 51f. (Penguin, 2003) ISBN 978-1-5519-2647-6
- ^ J. P. McEvoy and Oscar Zarate (2004). Introducing Quantum Theory. Totem Books. s. 114. ISBN 1-84046-577-8.
- ^ Van der Waerden, B. L. (1967). Sources of Quantum Mechanics (İngilizce). Mineola, New York: Dover Publications. ss. 261-276.
- ^ Werner Heisenberg'in kağıdı görüyorsanız, "Kuantum-Teorik Kinematik ve Mekanik İlişkiler Yeniden Yorumlamak", s 261-276
- ^ Nobel Prize Organization. "Erwin Schrödinger - Biographical". 24 Ocak 2016 tarihinde kaynağından arşivlendi. Erişim tarihi: 28 Mart 2014.
His great discovery, Schrödinger's wave equation, was made at the end of this epoch-during the first half of 1926.
- ^ ""Schrodinger Equation (Physics)," Encyclopædia Britannica ". 29 Mayıs 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 11 Haziran 2014.
- ^ W. Moore, Schrödinger: Life and Thought, Cambridge University Press (1989), p. 222. See p. 227 for Schrödinger's own words.
- ^ "Heisenberg's Nobel Prize citation". 16 Temmuz 2008 tarihinde kaynağından arşivlendi. Erişim tarihi: 11 Haziran 2014.
- ^ Heisenberg first published his work on the uncertainty principle in the leading German physics journal Zeitschrift für Physik: Heisenberg, W. (1927). "Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik". Z. Phys. 43 (3–4). ss. 172-198. Bibcode:1927ZPhy...43..172H. doi:10.1007/BF01397280.
- ^ ""Uncertainty principle," Encyclopædia Britannica". 9 Mayıs 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 11 Haziran 2014.
- ^ a b Linus Pauling, The Nature of the Chemical Bond, p. 47
- ^ ""Orbital (chemistry and physics)," Encyclopædia Britannica ". 4 Kasım 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 11 Haziran 2014.
- ^ ""Mechanics," Merriam-Webster Online Dictionary". 24 Ağustos 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 11 Haziran 2014.
- ^ "Field" 5 Ağustos 2014 tarihinde Wayback Machine sitesinde arşivlendi., Encyclopædia Britannica
- ^ Richard Hammond, The Unknown Universe, New Page Books, 2008. ISBN 978-1-60163-003-2
- ^ "The Physical World website". 4 Mart 2016 tarihinde kaynağından arşivlendi. Erişim tarihi: 11 Haziran 2014.
- ^ "The Nobel Prize in Physics 1933". Nobel Foundation. 14 Eylül 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 24 Kasım 2007.
- ^ Durrani; Ahmed, H. (2008). Nanosilicon. Vijay Kumar: Elsevier. s. 345. ISBN 978-0-08-044528-1.
Diğer parçalar
- Jim Al-Khalili (2003) Quantum: A Guide for the Perplexed. Weidenfield & Nicholson. ISBN 978-1780225340
- Chester, Marvin (1987) Primer of Quantum Mechanics. John Wiley. ISBN 0-486-42878-8
- Brian Cox and Jeff Forshaw (2011) The Quantum Universe. Allen Lane. ISBN 978-1-84614-432-5
- Richard Feynman (1985) QED: The Strange Theory of Light and Matter. Princeton University Press. ISBN 0-691-08388-6
- Ford, Kenneth (2005) The Quantum World. Harvard Univ. Press. Includes elementary particle physics.
- Ghirardi, GianCarlo (2004) Sneaking a Look at God's Cards, Gerald Malsbary, trans. Princeton Univ. Press. The most technical of the works cited here. Passages using algebra, trigonometry, and bra–ket notation can be passed over on a first reading.
- Tony Hey and Walters, Patrick (2003) The New Quantum Universe. Cambridge Univ. Press. Includes much about the technologies quantum theory has made possible. ISBN 978-0521564571
- Vladimir G. Ivancevic, Tijana T. Ivancevic (2008) Quantum leap: from Dirac and Feynman, across the universe, to human body and mind. World Scientific Publishing Company. Provides an intuitive introduction in non-mathematical terms and an introduction in comparatively basic mathematical terms. ISBN 978-9812819277
- N. David Mermin (1990) "Spooky actions at a distance: mysteries of the QT" in his Boojums all the way through. Cambridge Univ. Press: 110–176. The author is a rare physicist who tries to communicate to philosophers and humanists. ISBN 978-0521388801
- Roland Omnès (1999) Understanding Quantum Mechanics. Princeton Univ. Press. ISBN 978-0691004358
- Victor Stenger (2000) Timeless Reality: Symmetry, Simplicity, and Multiple Universes. Buffalo NY: Prometheus Books. Chpts. 5–8. ISBN 978-1573928595
- Martinus Veltman (2003) Facts and Mysteries in Elementary Particle Physics. World Scientific Publishing Company. ISBN 978-9812381491
- J. P. McEvoy and Oscar Zarate (2004). Introducing Quantum Theory. Totem Books. ISBN 1-84046-577-8
Dış bağlantılar

- "Microscopic World – Introduction to Quantum Mechanics." by Takada, Kenjiro, Emeritus professor at Kyushu University
- Quantum Theory. 24 Şubat 2009 tarihinde Wayback Machine sitesinde arşivlendi. at encyclopedia.com
- The spooky quantum
- The Quantum Exchange 26 Haziran 2014 tarihinde Wayback Machine sitesinde arşivlendi. (tutorials and open source learning software).
- Atoms and the Periodic Table 7 Nisan 2014 tarihinde Wayback Machine sitesinde arşivlendi.
- Single and double slit interference
- Time-Evolution of a Wavepacket in a Square Well 5 Ağustos 2014 tarihinde Wayback Machine sitesinde arşivlendi. An animated demonstration of a wave packet dispersion over time.
- Experiments with single photons An introduction into quantum physics with interactive experiments
- Carroll, Sean M. "Quantum Mechanics (an embarrassment)". Sixty Symbols. Brady Haran for the University of Nottingham. 17 Mayıs 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 11 Haziran 2014.
- Comprehensive animations 7 Temmuz 2015 tarihinde Wayback Machine sitesinde arşivlendi.