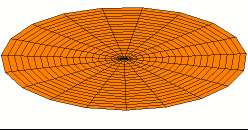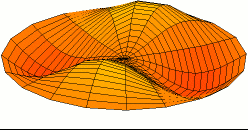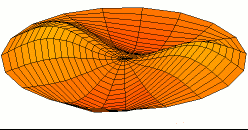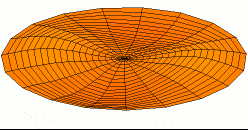
Kuantum harmonik salınıcı

Kuantum harmonik salınıcı, klasik harmonik salınıcın benzeşiğidir. Rastgele seçilmiş potansiyeli denge noktası civarında harmonik potansiyele yakınsanabildiğinden nicem mekanğindeki en önemli model sistemlerden biridir. Dahası, nicem mekaniğinde kesin analitik çözümü olan çok az sistemden biridir.

Parçacığın Hamilton işlevi (bir sistemin enerjisini momentumu ve konumuna bağlı olarak ifade etmeye yarayan işlev):

${\displaystyle {\hat {H}}={\frac {{\hat {p}}^{2}}{2m}}+{\frac {1}{2}}m\omega ^{2}{\hat {x}}^{2}\,,}$

m parçacığın kütlesi, ω açısal frekansı, ${\displaystyle {\hat {x}}=x}$ konum işlemcisi ve ${\displaystyle {\hat {p}}}$ momentum işlemcisidir. Momentum işlemcisi ise şu denklemle bulunur:

${\displaystyle {\hat {p}}=-i\hbar {\partial \over \partial x}\,.}$

Hamilton işlevindeki ilk ifade parçacığın olası hareket (kinetik) enerjisidir ve ikinci terim sırasıyla potansiyel enerji durumunu ifade eder. Zamandan bağımsız Schrödinger eşitliği;

${\displaystyle {\hat {H}}\left|\psi \right\rangle =E\left|\psi \right\rangle \,,}$

Yine de E zamandan bağımsız olan enerji düzeyini ve gerçek bir sayıyı ifade eder öz değeri olarak adlandırılabilir ve çözüm |ψ⟩ özdurumdaki enerji düzeyini gösterir.Öz değerinin eşitliği koordinat kökeninde dalga işlevi, ⟨x|ψ⟩ = ψ(x), bulmak için spektral yöntem kullanılarak türetilebilir. Görülür ki, çözümleri aynı kümedendir. Bu yöntem, miktarları;

${\displaystyle \psi _{n}(x)={\frac {1}{\sqrt {2^{n}\,n!}}}\cdot \left({\frac {m\omega }{\pi \hbar }}\right)^{1/4}\cdot e^{-{\frac {m\omega x^{2}}{2\hbar }}}\cdot H_{n}\left({\sqrt {\frac {m\omega }{\hbar }}}x\right),\qquad n=0,1,2,\ldots .}$

H_n işlevleri Hermit polinomlarını ifade eder;

${\displaystyle H_{n}(x)=(-1)^{n}e^{x^{2}}{\frac {d^{n}}{dx^{n}}}\left(e^{-x^{2}}\right)}$ . .

Enerji düzeylerinin eşitliği ise;

${\displaystyle E_{n}=\hbar \omega \left(n+{1 \over 2}\right)}$ . ’dir.

Bu enerji spekturumu üç nedenden dikkat edilmeye değerdir. Öncelikle enerjiler nicelenir, yani sadece ayrık enerji değerleri mümkündür (tam sayı ve yarısının toplamı ile ħω'ın çarpımı); bu nicem sistemlerinde, parçacık sınırlandığındaki sistemlerin genel özelliğidir. İkinci olarak, bu ayrık enerji düzeylerinde eşit olarak boşluk bırakılır, Bohr atom modelinin aksine ya da kutudaki parçacık gibi. Üçüncü olarak, ulaşılabilen en düşük enerji (n = 0 durumu, zemin durumu) potansiyel enerjiden büyüktür ancak hw/2'den küçüktür bu duruma sıfır noktası enerjisi denir. Heisenberg'ün belirsizlik ilkesine göre sıfır noktası enerjisi yüzünden, salınıcının zemin noktasındaki konumu ve momentumu klasik salınıcıda olduğu gibi düzgün değildir, ama dağılım çeşitliliği azdır. Sıfır noktası enerjisinin nicem alan kuramı ve nicem kütleçekimi içinde oldukça büyük önemi vardır. Zemin durumu olası özkütlesinin sıfır noktasında yoğunlaşması dikkate alınması gereken bir durumdur. Bu parçacığın beklendiği gibi düşük bir enerji ile zamanının çoğunu potansiyel kuyusunun dibinde geçirdiği anlamına gelir. Enerjinin artması ile birlikte, olası özkütle enerjinin potansiyel enerji ile uyuştuğu klasik dönüm noktalarında yoğunlaşır. Bu klasik harmonik salınıcı ile tutarlıdır, bunun için parçacık zamanının çoğunu en yavaş olduğu dönüm noktalarında harcar. Bu yüzden karşılanım ilkesi doğrudur.

Bu spektral yöntem, tekdüze bir yöntem olarak değerlendirilebilir.Paul Dirac tarafından geliştirilen yaradış-yokediş işlemci yöntemi türev denklemini çözmemize gerek kalmadan enerjinin öz değerini bulmamızı sağlar. Dahası, nicem alan kuramındaki birçok karışık problem için genellenebilir.Bu başlangıçtan sonra, işlemcileri a olarak ve a'nın bitiştirilmişi (adjoint), (a^†) olarak tanımlıyoruz,

${\displaystyle {\begin{aligned}a&={\sqrt {m\omega \over 2\hbar }}\left({\hat {x}}+{i \over m\omega }{\hat {p}}\right)\\a^{\dagger }&={\sqrt {m\omega \over 2\hbar }}\left({\hat {x}}-{i \over m\omega }{\hat {p}}\right)\end{aligned}}}$

Bu (${\displaystyle {\hat {x}}}$ ve ${\displaystyle {\hat {p}}}$) kullanmamızı sağlar,

${\displaystyle {\hat {x}}={\sqrt {\frac {\hbar }{2m\omega }}}(a+a^{\dagger })}$

${\displaystyle {\hat {p}}=i{\sqrt {\frac {m\omega \hbar }{2}}}(a^{\dagger }-a)~.}$

Operator a Hermit işlevi değildir, çünkü kendisi ve bitiştirilmişi eşit değildir. Yine de enerji öz durumu |n⟩, bu yaradış-yokediş işlemcileri tarafından işletildiğinde, şunu verir;

${\displaystyle a^{\dagger }|n\rangle ={\sqrt {n+1}}\,|n+1\rangle }$

${\displaystyle a|n\rangle ={\sqrt {n}}\,|n-1\rangle }$ .

Bu a nicemi silerken '(a^†)ın nicem salınıcı için nicemde bir enerjisi olduğunun ispatıdır, bu yüzden, yaradış-yokediş işlemcileri olarak anılırlar. Yukarıdaki ilişkilere göre, sayı işlemcisini de tanımlayabiliriz,N:

${\displaystyle N=a^{\dagger }a}$

${\displaystyle N\left|n\right\rangle =n\left|n\right\rangle }$.

Bu çeviriciler kolaylıkla kuralsal öndelenim (komütasyon) ilişkilerini elde etmemizi sağlar.,

${\displaystyle [a,a^{\dagger }]=1,\qquad [N,a^{\dagger }]=a^{\dagger },\qquad [N,a]=-a,}$

Hamilton işlemcileri şöyle gösterilebilir;

${\displaystyle H=\left(N+{\frac {1}{2}}\right)\hbar \omega ,}$

Yani, enerjinin öz durumu aynı zamanda N'nin öz durumudur. Öndelenim (Komütasyon) özellikleri ;

${\displaystyle {\begin{aligned}Na^{\dagger }|n\rangle &=\left(a^{\dagger }N+[N,a^{\dagger }]\right)|n\rangle \\&=\left(a^{\dagger }N+a^{\dagger }\right)|n\rangle \\&=(n+1)a^{\dagger }|n\rangle ,\end{aligned}}}$

Ve benzer olarak dir.

${\displaystyle Na|n\rangle =(n-1)a|n\rangle .}$

Bu şu anlama gelir; a |n⟩’e göre değişir, çarpımsal bir sabit, |n–1⟩, üretmek için ve (a^†) |n⟩’e göre değişir, |n+1⟩, sabitini üretmek için değişir. Bu yüzden, a düşürücü işlemci ve (a^†) yükseltici işlemcisi olarak da adlandırılır. Bu iki işlemciye yaradış-yokediş işlemcileri de denir. Nicem alan kuramında yaradış-yokediş işlemcileri olarak da adlandırılırlar çünkü enerjinin miktarına göre parçacık yaratıp yok ederler. Daha az enerjiyle başka bir öz durumu yaratmak için düşürücü işlemciyi kullanırız. Bu uygulamayı düşürücü işlemci de takip ederek, E = −∞) ‘a kadar enerji üretebilirmiş gibi gösterebiliriz . Ancak,

${\displaystyle n=\langle n|N|n\rangle =\langle n|a^{\dagger }a|n\rangle =\left(a|n\rangle \right)^{\dagger }a|n\rangle \geqslant 0,}$

En küçük öz sayısı 0’dır ve

${\displaystyle a\left|0\right\rangle =0}$..

Bu durumda, düşürücü işlemcinin sonraki uygulamaları öz durumu enerjilerine ek olarak 0’ı üretecektir.

${\displaystyle H\left|0\right\rangle ={\frac {\hbar \omega }{2}}\left|0\right\rangle }$

Son olarak, |0⟩ yükseltici işlemciyi ve uygun standartlaştırma faktörlerini çarparak sonsuz sayıda öz durumu enerji setleri üretiriz.

${\displaystyle \left\{\left|0\right\rangle ,\left|1\right\rangle ,\left|2\right\rangle ,...,\left|n\right\rangle ,...\right\}}$,

örneğin

${\displaystyle H\left|n\right\rangle =\hbar \omega \left(n+{\frac {1}{2}}\right)\left|n\right\rangle }$ ,

Enerji spektrumu ile uyumludur. Rastgele öz durumu |0⟩ ile şu şekilde ifade edilir,

${\displaystyle |n\rangle ={\frac {\left(a^{\dagger }\right)^{n}}{\sqrt {n!}}}|0\rangle }$ .

İspat:

${\displaystyle {\begin{aligned}\langle n|aa^{\dagger }|n\rangle &=\langle n|\left([a,a^{\dagger }]+a^{\dagger }a\right)|n\rangle =\langle n|\left(N+1\right)|n\rangle =n+1\\\Rightarrow a^{\dagger }|n\rangle &={\sqrt {n+1}}|n+1\rangle \\\Rightarrow |n\rangle &={\frac {a^{\dagger }}{\sqrt {n}}}|n-1\rangle ={\frac {\left(a^{\dagger }\right)^{2}}{\sqrt {n(n-1)}}}|n-2\rangle =\cdots ={\frac {\left(a^{\dagger }\right)^{n}}{\sqrt {n!}}}|0\rangle .\end{aligned}}}$

|0>’ın Zemin durumu a |0⟩ = 0 olarak gösterilir,

${\displaystyle {\begin{aligned}&\left\langle x\left|a\right|0\right\rangle =0~~~~~~~~~~\Longrightarrow \\&\left(x+{\frac {\hbar }{m\omega }}{\frac {d}{dx}}\right)\left\langle x|0\right\rangle =0~~~~~~\Longrightarrow \\&\left\langle x|0\right\rangle =\left({\frac {m\omega }{\pi \hbar }}\right)^{\frac {1}{4}}\exp \left(-{\frac {m\omega }{2\hbar }}x^{2}\right)=\psi _{0}~,\end{aligned}}}$

Ve bu yüzden

${\displaystyle \langle x|a^{\dagger }|0\rangle =\psi _{1}~,}$

önceki bölümdeki gibi.

Nicem harmonik salınıcı, uzunluk ve enerji için problem kolaylaştıracak doğal ölçeklere sahiptir. Boyutsuzlaştırmayla bulunabilir. Sonuç bize eğer enerjisini ħω ile mesafeyi √ħ/(mω) ile ölçersek Schrödinger’in denklemi şöyle olur;

${\displaystyle H=-{1 \over 2}{d^{2} \over dx^{2}}+{1 \over 2}x^{2},}$

Enerji öz değerleri ve işlevleri olurken

${\displaystyle \psi _{n}(x)\equiv \left\langle x|n\right\rangle ={1 \over {\sqrt {2^{n}n!}}}\pi ^{-1/4}{\hbox{exp}}(-x^{2}/2)H_{n}(x),}$

${\displaystyle E_{n}=n+{\tfrac {1}{2}},}$

H_n(x) Hermit polinomları demektir. Karışıklıktan kaçınmak için, bu makalede “doğal birmler”`i benimsememeliyiz. Ancak bu birimler çoğunlukla hesaplamalarda karışıklığı atlandığından kolay gelir.

Nicem mekaniğinin faz-uzayı denklemleştirilmesinde, nicem harmonik salınıcı için olasılık dağılımında birkaç farklı temsili çözümler yazılabilir. En yaygın kullanılanı ise Wigner işlevidir.

Çözümü şöyledir;

${\displaystyle F_{n}(u)={\frac {(-1)^{n}}{\pi \hbar }}L_{n}\left(4{\frac {u}{\hbar \omega }}\right)e^{-2u/\hbar \omega }~,}$

${\displaystyle u={\frac {1}{2}}m\omega ^{2}x^{2}+{\frac {p^{2}}{2m}}}$

Bu örnek bize gösterir ki Wigner-Weyl dönüşümü sayesinde Hermit ve Laguerre polinomları birbiri ile ilişkilidir.

Tek boyutlu harmonik salınıcı N-boyutluya kolaylıkla genellenebilir, N=1,2,3,…olabilir. Bir boyutta, parçacığın konumu tek koordinat x ile belirlenebilir. N boyutta ise, bu N koordinat ile yer değişir, x₁, ..., x_N. Buna göre her konumun momentumunu olduğunu düşünürsek, momentum p₁, ..., p_N şeklinde gösterilebilir. Bu iki işlemci arasındaki kuralsal değiştirme ilişkisi şöyledir;

${\displaystyle {\begin{matrix}\left[x_{i},p_{j}\right]&=&i\hbar \delta _{i,j}\\\left[x_{i},x_{j}\right]&=&0\\\left[p_{i},p_{j}\right]&=&0\end{matrix}}}$.

Sistemin Hamilton işlevi,

${\displaystyle H=\sum _{i=1}^{N}\left({p_{i}^{2} \over 2m}+{1 \over 2}m\omega ^{2}x_{i}^{2}\right)}$.

Bu Hamilton işlevi formunun açıkça gösterdiği gibi, N-boyutlu harmonik salınıcı N tane bağımsız, aynı kütle ve yay sabitine sabit salınıcı ile tamamıyla aynı şeydir. Bu durumda, nicelikler, x₁, ..., x_N, N tane parçacığın yerini belirtirler. Bu ${\displaystyle r^{2}}$ potansiyelinin, potansiyel enerjinin koordinatlara göre ayrılmasını sağlayan uygun bir özelliğidir. Gözlemler bu çözümü doğrular niteliktedir. Belirli nicem sayıları seti için {n} N-boyutlu salınıcının enerji öz işlevleri 1-boyutlu öz işlevi gibi ifade edilir:

${\displaystyle \langle \mathbf {x} |\psi _{\{n\}}\rangle =\prod _{i=1}^{N}\langle x_{i}|\psi _{n_{i}}\rangle }$

Yaradış-yokediş işlemci yönteminde, N tane yaradış-yokediş işlemci serisi belirlenir,

${\displaystyle {\begin{matrix}a_{i}&=&{\sqrt {m\omega \over 2\hbar }}\left(x_{i}+{i \over m\omega }p_{i}\right)\\a_{i}^{\dagger }&=&{\sqrt {m\omega \over 2\hbar }}\left(x_{i}-{i \over m\omega }p_{i}\right)\end{matrix}}}$.

Tek-boyutlu duruma göre benzer işlem uygulanırsa, burada da a_i ve a^†_i alçaltan ve yükselten işlemciler diyebiliriz. Hamilton işlevi,

${\displaystyle H=\hbar \omega \,\sum _{i=1}^{N}\left(a_{i}^{\dagger }\,a_{i}+{\frac {1}{2}}\right).}$

Hamilton işlevi, dinamik eşbakışım(simetri) grubunun altındaki U(N) (boyutların bölünmez grubu) sabit niceliktir, şöyle tanımlanır,

${\displaystyle U\,a_{i}^{\dagger }\,U^{\dagger }=\sum _{j=1}^{N}a_{j}^{\dagger }\,U_{ji}\quad {\hbox{for all}}\quad U\in U(N),}$

burada ${\displaystyle U_{ji}}$. U(N)'in dizey temsil elementidir.

Sistemlerin enerji düzeyleri

${\displaystyle E=\hbar \omega \left[(n_{1}+\cdots +n_{N})+{N \over 2}\right]}$.

${\displaystyle n_{i}=0,1,2,\dots \quad ({\hbox{the energy level in dimension }}i).}$

Tek-boyutlu durumdaki gibi enerji nicemlenir. Taban durum enerjisi tek boyutlu durum enerjisinin N katıdır, bu benzerliği beklendiği gibi N tane bağımsız tek-boyutlu salınıcı için kullanırız. Bunun dışında bir fark daha vardır tek-boyutlu durumda, tüm enerji düzeyleri farklı bir nicem değeri ifade eder. N-boyutta, zemin durumu hariç, enerji düzeyleri bozulur, bu yüzden bazı durumlarda aynı enerji olur. Çakışıklık (degeneracy) diğer işlemlere oranla kolayca hesaplanabilir. Örnek olarak, 3-boyutlu bir durumu varsayalım: n = n₁ + n₂ + n₃ olarak tanımlayalım. Tüm durumlar aynı n ile eşit enerjiye sahip olur. Bilinen n için, belirli bir n₁ seçilir, n₂ + n₃ = n − n₁ 'dir. n − n₁ + 1'in olası grupları {n₂, n₃}'dir. n₂ 0'dan n − e kadar değerler alır ve tüm n₂ değerli için n₃ ayarlanır. Çakışıklığın (degeneracy) derecesi şöyle hesaplanır.

${\displaystyle g_{n}=\sum _{n_{1}=0}^{n}n-n_{1}+1={\frac {(n+1)(n+2)}{2}}}$

Genel N ve n için denklem şudur; [gn  :${\displaystyle g_{n}={\binom {N+n-1}{n}}}$ bölünmez grubun temsili indirgenemez eşbakışımlı (simetrik) n'inci kuvvetidir ]

Verilen özel durum N = 3, tamamen bu eşitliği takip edilerek bulunur. Ancak bu sadece fark edilebilir parçacıklar için doğrudur ya da N-boyuttaki bir parçacık için doğrudur. N tane bozon için geçerli durumdaki çakışıklık çizelgesi tam sayıları kullanarak yazıldığında N'den küçük ya da N'e eşittir.

${\displaystyle g_{n}=p(N_{-},n)}$

Bu durum N nicemini ${\displaystyle \sum _{k=0}^{\infty }kn_{k}=n}$ ve ${\displaystyle \sum _{k=0}^{\infty }n_{k}=N}$, sınırlayınca ortaya çıkar.

Küresel eşbakışımlı üç boyutlu harmonik salınıcı Scrödinger eşitliği değerlerin ayrılığı ile açıkça çözülebilir.Bu işlem, hidrojen-benzeri atom probleminin benzeşiğidir ve küresel eşbakışımlı potansiyeli ile,

${\displaystyle V(r)={1 \over 2}\mu \omega ^{2}r^{2},}$

${\displaystyle \mu }$ problemin kütlesidir. (Çünkü m manyetik nicem sayısı olarak kullanılacak, bu yüzden kütle ${\displaystyle \mu }$ ile ifade edilecek.).Çözüm okunur

${\displaystyle \psi _{klm}(r,\theta ,\phi )=N_{kl}r^{l}e^{-\nu r^{2}}{L_{k}}^{(l+{1 \over 2})}(2\nu r^{2})Y_{lm}(\theta ,\phi )}$

${\displaystyle N_{kl}={\sqrt {{\sqrt {\frac {2\nu ^{3}}{\pi }}}{\frac {2^{k+2l+3}\;k!\;\nu ^{l}}{(2k+2l+1)!!}}}}\,}$birimboylandırım sabitidir.

${\displaystyle \nu \equiv {\mu \omega \over 2\hbar }}$

${\displaystyle {L_{k}}^{(l+{1 \over 2})}(2\nu r^{2})}$

Laguerre polinomu olarak genellenebilirler. k negatif olmayan bir tam sayıdır.

${\displaystyle Y_{lm}(\theta ,\phi )\,}$ küresel harmonik işlevi.

${\displaystyle \hbar }$ indirgenmiş Planck sabiti: . : ${\displaystyle \hbar \equiv {\frac {h}{2\pi }}}$ Enerjinin özdeğeri,

${\displaystyle E=\hbar \omega \left(2k+l+{\frac {3}{2}}\right)~.}$

Enerji genelde tek bir nicem sayısıyla ifade edilir.

${\displaystyle n\equiv 2k+l~.}$

Çünkü k tüm ${\displaystyle l=0,2...,n-2,n}$ ve ${\displaystyle l=1,3...,n-2,n}$ değerleri için negatif olmayan bir tam sayıdır, Manyetik nicem sayısı m, ${\displaystyle -l\leq m\leq l}$’e uyan bir tam sayıdır, tüm n ve l değerleri için bu yüzden n’in bozulma düzeyi,

${\displaystyle \sum _{l=\ldots ,n-2,n}(2l+1)={(n+1)(n+2) \over 2}~,}$ ‘dir.

n’in çift ya da tek olmasına göre toplam 0 ya da 1’den başlar. Bu sonuç üsteki boyut denklemine göre ve SU(3)’ün eşbakışımlı temsili ile ilgili çakışıklık grubudur.

Harmonik salınıcı görüşünü birçok parçacığın kafesi olarak genişletebiliriz. Tek boyutlu nicem mekanik harmonik zincirinde N tane özdeş atom ele alınır. Bu kafesin en basit nicem mekaniksel modelidir ve bundan nasıl fononların yayıldığını görürüz. Bu model için gelişecek olan biçim iki ve üç boyutlu olarak genellenebilir. Bundan önceki bölümde, denge konumlarına göre ölçüm yaparak kütlelerin konumları olan ${\displaystyle x_{1},x_{2},...}$’yi bulduk (i.e. ${\displaystyle x_{i}=0}$ eğer parçacık denge konumundaysa.) İki ya da daha fazla boyutta, ‘${\displaystyle x_{i}}$ler yöneyli değerlerdir. Sistemin Hamilton işlevi

${\displaystyle \mathbf {H} =\sum _{i=1}^{N}{p_{i}^{2} \over 2m}+{1 \over 2}m\omega ^{2}\sum _{\{ij\}(nn)}(x_{i}-x_{j})^{2}\ }$

m, her atomun ayrı kütlesi (hepsinin eşit olduğunu var sayılır) ve i. atom için ve en yakın komşuları için (nn) ${\displaystyle \,x_{i}}$ ve ${\displaystyle \,p_{i}}$ konum ve momentum işlemcileridir. Ancak, beklendiği gibi, kafeste dalgalar parçacık gibi davrandığı görünebilir. Dalgaların hareketlerinde, dalgayöneyi normal modları kullanılarak parçacıkların koordinat değerleri yerine Fourier uzayı özel olarak işlenir. Normal modların sayıları parçacıklarla aynıdır ancak Fourier uzayı sistemin tekrarsıklığı için oldukça kullanışlıdır. N'in “normal koordinatlar” seti ${\displaystyle \,Q_{k}}$ xs'in ayrık Fourier dönüşümleri olarak tanımlanır ve N “eşlenik momentumları” Π ps'nin Fourier dönüşümleri olarak tanımlanır

${\displaystyle Q_{k}={1 \over {\sqrt {N}}}\sum _{l}e^{ikal}x_{l}}$

${\displaystyle \Pi _{k}={1 \over {\sqrt {N}}}\sum _{l}e^{-ikal}p_{l}.}$

${\displaystyle \,k_{n}}$ fononun dalga numarasıdır, yani 2 π'nin dalga boyuna bölünmesidir. Nicelikli değerlerdir, çünkü atom sayısı sonludur. Bu seçim istenilen değiştirme ilişkilerinin gerçek boşluk ya da dalgayöneyi uzayını alıkoyar.

${\displaystyle {\begin{aligned}\left[x_{l},p_{m}\right]&=i\hbar \delta _{l,m}\\\left[Q_{k},\Pi _{k'}\right]&={1 \over N}\sum _{l,m}e^{ikal}e^{-ik'am}[x_{l},p_{m}]\\&={i\hbar \over N}\sum _{m}e^{iam\left(k-k'\right)}=i\hbar \delta _{k,k'}\\\left[Q_{k},Q_{k'}\right]&=\left[\Pi _{k},\Pi _{k'}\right]=0\end{aligned}}}$

Genel olarak

${\displaystyle {\begin{aligned}\sum _{l}x_{l}x_{l+m}&={1 \over N}\sum _{kk'}Q_{k}Q_{k'}\sum _{l}e^{ial\left(k+k'\right)}e^{iamk'}=\sum _{k}Q_{k}Q_{-k}e^{iamk}\\\sum _{l}{p_{l}}^{2}&=\sum _{k}\Pi _{k}\Pi _{-k}.\end{aligned}}}$

Potansiyel enerji şöyle gösterilebilir;

${\displaystyle {1 \over 2}m\omega ^{2}\sum _{j}(x_{j}-x_{j+1})^{2}={1 \over 2}\omega ^{2}\sum _{k}Q_{k}Q_{-k}(2-e^{ika}-e^{-ika})={1 \over 2}\sum _{k}{\omega _{k}}^{2}Q_{k}Q_{-k},}$

${\displaystyle \omega _{k}={\sqrt {2\omega ^{2}(1-\cos(ka))}}.\ }$

Hamilton işlevi dalgayöneyli olarak şöyle yazılabilir;

${\displaystyle \mathbf {H} ={1 \over {2m}}\sum _{k}\left({\Pi _{k}\Pi _{-k}}+m^{2}\omega _{k}^{2}Q_{k}Q_{-k}.\right)}$

Konum değerleri arasındaki bağlantı dikkate alınacak bir dönüşüme uğramıştır; Eğer Qlar ve Πler hermitian(değiller) olsalar, dönüşmüş Hamilton işlevi N eşlememiş harmonik salınıcıya eşit olur. Kolaylık için, sınır durumunu periyoduk olarak belirleriz, atomun (N+1). Eşitliği ilk atoma eşittir. Fiziksel olarak, bu zincirin sonuna eklenir. Sonuç veren nicelik

${\displaystyle k=k_{n}={2n\pi \over Na}\quad {\hbox{for}}\ n=0,\pm 1,\pm 2,...,\pm {N \over 2}.\ }$

Üst düzey bağ n en az (minimum) dalga boyundan gelir, yukarıda tartışıldığı gibi kafes boşluğu, a,`nın ik katıdır. Harmonik salınıcının öz değeri ya da ${\displaystyle \omega _{k}}$ için enerji düzeyi:

${\displaystyle E_{n}=\left({1 \over 2}+n\right)\hbar \omega _{k}\quad \quad \quad n=0,1,2,3......}$

Eğer sıfır noktası enerjisini yoksayarsak düzeyler şöyle sıralanır: ħω, 2ħω, 3ħω, ...

ħω, 2ħω, 3ħω, ...

ħω’ ħωnin gerçek enerji değeri, sonraki enerji düzeyinin harmonik salınıcı kafesine tedarik edilmelidir. Elektromanyetik alan sayısal olarak belirlendiğinde foton durumunun kıyasında titreşim enerjisinin nicemine fonon denir. Tüm nicem sistemleri dalgamsı ya da parçacığımsı özellik gösterirler. Fononun parçacığımsı özellikleri ikinci nicelemede en iyi anlaşılır ve işlemci teknikleri sonra tanımlanır.

• Çift atomlu molekülün titreşimi iki cisimli nicem harmonik salınıcına örnektir. Açısal tekrarsıklığı şöyle bulunur,
• :${\displaystyle \omega ={\sqrt {\frac {k}{\mu }}}}$
• ${\displaystyle \mu }$ indirgenmiş kütledir ve = m1m2/(m1+m²) olarak iki atomun kütlesi ile ilişkilidir.
• Hooke'un atomu basit bir helyum atom modelidir nicem harmonik salınıcında da kullanılır.
• Üstte tartışılan model fononlar,
• Kütle ve yükün değişmeyen manyetik alanda olması açısal momentumlu tek boyutlu nicem harmonik salınıcına ya da iki boyutlu nicem harmonik salınıcına bir örnektir.

İngilizce vikipedi