
Trigonometri, üçgenlerin açıları ile kenarları arasındaki bağıntıları konu edinen matematik dalı. Trigonometri, sinüs ve kosinüs gibi trigonometrik işlevlerin (fonksiyon) üzerine kurulmuştur ve günümüzde fizik ve mühendislik alanlarında sıkça kullanılmaktadır.

Geometride, elips bir koninin bir düzlem tarafından kesilmesi ile elde edilen düzlemsel, ikinci dereceden, kapalı eğridir.

Günlük kullanımıyla küre kusursuz simetriye sahip geometrik bir nesnedir, bir yüzeydir; üç boyutlu Öklit uzayında (R3) yatar.

Matematikte sinüs, trigonometrik bir fonksiyon. Sin kısaltmasıyla ifade edilir.

 Kartezyen çarpımındaki
Kartezyen çarpımındaki
- her sıralı ikilinin Öklid düzlemindeki bir noktaya ve
- birinci dereceden iki değişkenli her bir polinomun düzlemdeki bir doğruya, birebir eşlenmesi ile oluşturulan cebirsel geometrik yapıya Kartezyen koordinat sistemi veya Dik eksenler sistemi adı verilir. Öklid geometrisinin bir modelidir. Koordinat eksenleri x ve y eksenidir bunlar 0 da çakışır. Çakışılan yere sıfır noktası (orijin) adı verilir.

Trigonometrik fonksiyonlar, matematikte bir açının işlevi olarak geçen fonksiyonlardır. Geometride üçgenleri incelerken ve periyodik olarak tekrarlanan olayları incelerken sıklıkla kullanılırlar. Genel olarak bir açısı belirli dik üçgenlerde herhangi iki kenarın oranı olarak belirtilirler, ancak birim çemberdeki belirli doğru parçalarının uzunlukları olarak da tanımlanabilirler. Daha çağdaş tanımlarda sonsuz seriler veya belirli bir türevsel denklemin çözümü olarak geçerler.

Matematikte kutupsal koordinat sistemi veya polar koordinat sistemi, noktaların birer açı ve Kartezyen koordinat sistemindeki orijinin eşdeğeri olup "kutup" olarak bilinen bir merkez noktaya olan uzaklıklar ile tanımlandığı, iki boyutlu bir koordinat sistemidir. Kutupsal koordinat sistemi, matematik, fizik, mühendislik, denizcilik, robot teknolojisi gibi birçok alanda kullanılır. Bu sistem, iki nokta arasındaki ilişkinin açı ve uzaklık ile daha kolay ifade edilebildiği durumlar için özellikle kullanışlıdır. Kartezyen koordinat sisteminde, böyle bir ilişki ancak trigonometrik formüller ile bulunabilir. Kutupsal denklemler, çoğu eğri tipi için en kolay, bazıları içinse yegâne tanımlama yöntemidir.

Üç boyutlu uzay (3D); en, boy ve derinlik algılarının hepsinin birden var olduğu ortam. Cisimler; uzunluk, genişlik ve derinliği ile gösterebiliyorsa bu durumda üç boyuttan bahsedilebilir.

Tanjant, trigonometrik bir fonksiyondur. "tan" ile ifade edilir.

Yarıçap, bir daire veya kürenin özeğinin (merkezinin) çemberine olan mesafesidir. Çapın yarısına eşittir.

Logaritmik spiral, doğada sık rastlanan bir spiral çeşididir. İlk olarak 17. yüzyılda René Descartes ve Jakob Bernoulli tarafından tanımlanmış ve incelenmiştir. Bernoulli bu eğriye, kendine özgü matematiksel özelliklerinden dolayı, spira mirabilis adını vermiş ve mezar taşına bir logaritmik spiral oyulmasını vasiyet etmiştir.

Hiperbolik spiral, kutupsal koordinat sisteminde

Açısal hız, bir objenin birim zamandaki açısal olarak yer değiştirme miktarına verilen isimdir. Açısal hız vektörel olup bir cismin bir eksen üzerindeki dönüş yönünü ve hızını verir. Açısal hızın SI birimi radyan/saniyedir, ancak başka birimlerde de ölçülebilir. Açısal hız genellikle omega sembolü ile gösterilir. Açısal hızın yönü genellikle dönüş düzlemine diktir ve sağ el kuralı ile bulunabilir.

Geometride tetrahedron veya dört yüzlü, dört üçgen yüzden oluşan bir çokyüzlüdür (polihedron), her köşesinde üç üçgen birleşir. Düzgün dört yüzlü dört üçgenin eşkenar olduğu bir dört yüzlüdür ve Platonik cisimlerden biridir. Dörtyüzlü, dört yüzü olan tek konveks çokyüzlüdür. Tetrahedron isminin sıfat hali "tetrahedral"dır.

Matematikte sıfır noktası (orijin) düz uzayda O harfi ile gösterilen özel bir noktadır. Kartezyen eksenler sisteminde eksenlerin kesiştiği nokta sıfır noktasıdır. Düz uzayda sıfır noktası herhangi bir uygun nokta olarak seçilebilir. Bu seçim işlem sonucunda herhangi bir değişikliğe yol açmayacaktır. Sıfır noktası seçilirken genellikle yapılacak işleme göre uygun olan yer seçilir.

Birim çember Matematikte, yarıçapı bir birim olan çembere birim çember denir. Çoğunlukla, özellikle trigonometride, Öklid düzlemine göre Kartezyen koordinat sisteminde, merkezi orijin üzerinde (0,0) olan ve yarıçapı bir birim olan çemberdir. n birim çember sıklıkla S1; olarak ifade edilir. Genellikle daha büyük boyutları ise birim küredir. (x, y) birim çember üzerinde bir nokta olduğunda, |x| ve |y|, dik olan ve hipotenüsü bir olan üçgenin diğer kenar uzunluklarıdır. Bu nedenle, Pisagor teoremine göre, x ve y bu denklemi karşılamaktadır.


Geometride, Thales teoremi, A, B ve C, AC çizgisinin bir çap olduğu bir daire üzerinde farklı noktalar ise, ∠ABC açısının bir dik açı olduğunu belirtir. Thales teoremi, çevre açı teoreminin özel bir durumudur ve Öklid'in Elemanlar adlı eserinin üçüncü kitabında 31. önermenin bir parçası olarak bahsedilmiş ve kanıtlanmıştır. Genellikle, teoremin keşif için şükran kurbanı olarak bir öküz sunduğu söylenen Miletli Thales'e atfedilir, ancak bazen Pisagor'a da atfedilir.

Çıkış düğümü boylamı, bir nesnenin uzaydaki yörüngesini belirtmek için kullanılan yörünge ögelerinden biridir. Belirtilen bir referans düzleminde ölçüldüğü gibi, boylamın orijini olarak adlandırılan belirli bir referans yönünden çıkış düğümün yönüne olan açıdır. Çıkış düğümü, bitişik görüntüde görüldüğü gibi, nesnenin yörüngesinin referans düzleminden geçtiği noktadır. Yaygın olarak kullanılan referans düzlemleri ve boylamın kökenleri şunları içerir:
- Yer merkezli yörüngeler için, referans düzlemi olarak Dünya'nın ekvator düzlemi ve boylamın başlangıcı olarak Koç'un ilk noktası. Bu durumda boylam, çıkış düğümün sağ açıklığı (RAAN) olarak da adlandırılır. Açı, Koç'un ilk noktasından düğüme doğuya doğru ölçülür. Bir alternatif, uzay aracının ekvatoru geçtiği yerel ortalama zamana dayanan, çıkış düğümün yerel saatidir (LTAN). Diğer gezegenlerin etrafındaki uydular için de benzer tanımlar mevcuttur.
- Güneş merkezli yörüngeler için, referans düzlemi olarak ekliptik ve boylamın başlangıcı olarak Koç'un ilk noktası. Açı, Koç'un ilk noktasından düğüme kadar saat yönünün tersine ölçülür.
- Güneş Sistemi dışındaki yörüngeler için, referans düzlemi olarak ilgi noktasında gökküresine teğet olan düzlem ve kuzey gökyüzü düzlemine) boylamın kökeni olarak. Açı, kuzeyden düğüme doğuya doğru ölçülür., pp. 40, 72, 137; , chap. 17.
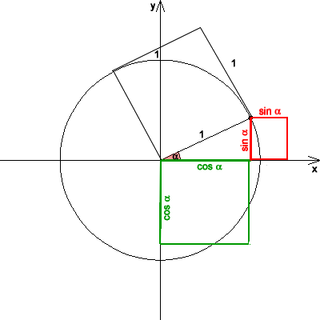
Pisagor trigonometrik özdeşliği, daha basit ifadeyle Pisagor özdeşliği olarak da adlandırılır, Pisagor teoremini trigonometrik fonksiyonlar cinsinden ifade eden bir özdeşliktir. Açıların toplam formülleri ile birlikte, sinüs ve kosinüs fonksiyonları arasındaki temel bağıntılardan biridir. Özdeşlik şu şekildedir:




























