
Matematiğin bir alt dalı olan Geometride bir eşkenar dörtgen, dört kenarlı ve tüm kenar uzunlukları birbirine eşit bir dörtgendir. Oyun kâğıtlarında görülen eşkenar dörtgene karo, bu şekle sahip olan haplara lozanj, bu şekle sahip olan beyzbol oyun sahasına diamond (elmas) denir.

Çemberlerde Thales teoremi, alınan A, B ve C noktalarının bir çember üzerinde ve AC doğrusunun bu çemberin çapı olması durumunda, ABC açısının dik açı olacağını belirten geometri teoremi. Thales teoremi çevre açı kurallarının özel bir hâlidir. Adını Thales'ten alan teorem, genellikle ona atfedilir ancak bazı yerlerde Pisagor'la da ilişkilendirilir.

Geometride, Thales teoremi, A, B ve C, AC çizgisinin bir çap olduğu bir daire üzerinde farklı noktalar ise, ∠ABC açısının bir dik açı olduğunu belirtir. Thales teoremi, çevre açı teoreminin özel bir durumudur ve Öklid'in Elemanlar adlı eserinin üçüncü kitabında 31. önermenin bir parçası olarak bahsedilmiş ve kanıtlanmıştır. Genellikle, teoremin keşif için şükran kurbanı olarak bir öküz sunduğu söylenen Miletli Thales'e atfedilir, ancak bazen Pisagor'a da atfedilir.

Gnomon teoremi, bir gnomon'da meydana gelen belirli paralelkenarların eşit büyüklükte alanlara sahip olduğunu belirtir. Gnomon, geometride benzer bir paralelkenarı daha büyük bir paralelkenarın bir köşesinden çıkararak oluşturulan bir düzlem şeklidir; veya daha genel olarak, belirli bir şekle eklendiğinde, aynı şekle sahip daha büyük bir şekil oluşturan bir şekildir.

Öklid geometrisinde, Batlamyus teoremi, bir kirişler dörtgeninin dört kenarı ile iki köşegeni arasındaki bir ilişkiyi gösteridir. Teorem, Yunan astronom ve matematikçi Batlamyus'un adını almıştır. Batlamyus, teoremi astronomiye uyguladığı trigonometrik bir tablo olan kirişler tablosunu oluşturmaya yardımcı olarak kullandı.

Geometride, Brahmagupta teoremi, eğer bir kirişler dörtgeni ortodiyagonal ise, o zaman köşegenlerin kesişme noktasından bir kenara çizilen dikmenin karşı kenarı daima ikiye böldüğünü belirtir. Adını Hint matematikçi Brahmagupta'dan (598-668) almıştır.

Geometride Brianchon teoremi, bir konik kesit etrafındaki bir altıgen ile sınırlandırıldığında, ana köşegenlerinin tek bir noktada kesiştiğini belirten bir teoremdir. Adını Fransız matematikçi Charles Julien Brianchon'dan (1783–1864) almıştır.
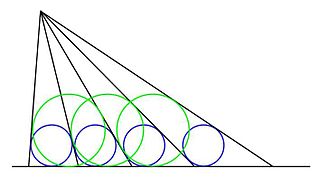
Geometride, eş iç teğet çemberler teoremi bir Japon Sangaku'sundan türetilir ve aşağıdaki yapıya ilişkindir: belirli bir noktadan belirli bir çizgiye bir dizi ışın çizilir, öyle ki bitişik ışınlar ve taban çizgisi tarafından oluşturulan üçgenlerin iç teğet çemberleri eşittir. Çizimde eş mavi çemberler, açıklandığı gibi ışınlar arasındaki mesafeyi tanımlar.

Leonhard Euler (1707–1783) adını taşıyan Euler dörtgen teoremi veya Euler'in dörtgenler yasası, dışbükey bir dörtgenin kenarları ile köşegenleri arasındaki ilişkiyi açıklar. Pisagor teoreminin genellemesi olarak görülebilecek Paralelkenar yasasının bir genellemesidir. Bu nedenle Pisagor teoreminin dörtgenler açısından yeniden ifade edilmesi bazen Euler-Pisagor teoremi olarak adlandırılır.

Fransız matematikçi Pierre-Leon Anne'in (1806-1850) adını taşıyan Anne teoremi, dışbükey dörtgen içindeki belirli alanların eşitliğini tanımlayan Öklid geometrisinden bir teoremdir.

Öklid geometrisinde, Batlamyus eşitsizliği, düzlemde veya daha yüksek boyutlu bir uzayda dört nokta tarafından oluşturulan altı uzunluğu ilişkilendirir. Herhangi bir A, B, C ve D noktası için aşağıdaki eşitsizliğin geçerli olduğunu belirtir:
 .
.
Leonhard Euler'in temel dörtgen geometrisindeki birçok sonucundan biri, iç içe uzanan iki belirli çember için Öklid düzleminde, hem daha büyük çemberin kirişler dörtgeni hem de daha küçük olana teğet olan bir teğetler dörtgeni olan bir dışbükey dörtgen bulunması problemiyle ilgilidir. Euler bunun için, dairenin merkezi ile bir düzlem üçgenin merkezi arasındaki mesafeye ilişkin teoremindekiyle yakından ilişkili olan bir denklem buldu. Denklemin ilk yayınlanmış sunumu ve türetilmesi, Euler'in sekreteri Nikolaus Fuß tarafından 1798'de sağlandı.

Geometride, çift merkezli (bicentric) çokgen, teğet bir çokgendir ve aynı zamanda döngüsel yani kirişler dörtgenidir - yani, çokgenin her köşesinden geçen bir çevrel çember içine çizilmiştir. Tüm üçgenler ve tüm düzgün çokgenler çift merkezlidir. Öte yandan, kenarları eşit olmayan bir dikdörtgen çift merkezli değildir, çünkü hiçbir çember dört kenara da teğet olamaz.

Öklid geometrisinde, bir çift merkezli dörtgen, hem bir iç teğet çembere hem de çevrel çembere sahip olan bir dışbükey (konveks) dörtgendir. Bu çemberlerin çevreleri, yarıçapları ve merkezlerine sırasıyla iç çap (inradius) ve çevrel çap (circumradius), iç merkez (incenter) ve çevrel merkez (circumcenter) denir. Tanımdan, çift merkezli dörtgenlerin hem teğetler dörtgeninin hem de kirişler dörtgeninin tüm özelliklerine sahip olduğu anlaşılmaktadır. Bu dörtgenler için diğer isimler kiriş-teğet dörtgeni ve iç teğet ve dış teğet dörtgenidir. Ayrıca nadiren çift çemberli dörtgen ve çift işaretlenmiş dörtgen olarak adlandırılmıştır.

Geometride Harcourt teoremi, kenar uzunluklarının bir fonksiyonu olarak ve kendi iç teğet çemberine teğet olan rastgele bir doğrudan köşelerinin dikey uzunluklarının bir fonksiyonu olarak üçgenin alanı ile ilgili bir formüldür. Teorem adını İrlandalı bir profesör olan J. Harcourt'tan almıştır.

Kesişen kirişler teoremi veya sadece kiriş teoremi, bir çember içinde kesişen iki kiriş tarafından oluşturulan dört doğru parçasının ilişkisini tanımlayan temel geometrideki bir ifadedir. Her bir kirişteki doğru parçalarının uzunluklarının çarpımlarının eşit olduğunu belirtir. Öklid'in Unsurlarının 3. kitabının 35. önermesidir.
Dışbükey bir kirişler çokgeni, herhangi bir şekilde üçgenlere ayrıldığında ve bu şekilde oluşturulan her üçgene bir iç teğet çember çizildiğinde Japon teoremi, bu üçgenlerin iç teğet çemberlerinin yarıçapları toplamının, seçilen üçgenlemeden bağımsız bir şekilde sabit olduğunu belirtir. Bu teorem, Carnot teoremi kullanılarak kanıtlanabilir. Japon matematikçilerin eski bir geleneğine göre, bu teorem 1800'de tanrıları ve yazarı onurlandırmak için bir Japon tapınağına asılan tabletlere yazılmış bir Sangaku problemiydi.

Yedi çember teoremi, Öklid düzlemindeki yedi adet çemberin belirli bir düzenlemesi hakkında bir geometri teoremidir. Bu teoreme göre, her biri iki komşusuna ve yedinci bir dış çembere teğet olan altı çemberden oluşan bir zincir verildiğinde, yedinci çember üzerindeki teğet noktalarının karşıt çiftlerini birleştiren üç doğru aynı noktadan geçer. Teorem, yalnızca temel geometrik ilkeler kullanılarak ifade edilip ispatlanabiliyor olsa da 1974'e kadar keşfedilememiştir.

Öklid geometrisinde, bir kirişler dörtgeni veya çembersel dörtgen veya çevrimsel dörtgen, köşeleri tek bir çember üzerinde bulunan bir dörtgendir. Bu çembere çevrel çember denir ve köşelerin aynı çember içinde olduğu söylenir. Çemberin merkezi ve yarıçapı sırasıyla çevrel merkez ve çevrel yarıçap olarak adlandırılır. Bu dörtgenler için kullanılan diğer isimler eş çember dörtgeni ve kordal dörtgendir, ikincisi, dörtgenin kenarları çemberin kirişleri olduğu içindir. Genellikle dörtgenin dışbükey (konveks) olduğu varsayılır, ancak çapraz çevrimsel dörtgenler de vardır. Aşağıda verilen formüller ve özellikler dışbükey durumda geçerlidir.





















