
Akışkanlar mekaniği, akışkanların davranışlarını ve onlara etkiyen kuvvetleri inceleyen fizik dalı. Makine, inşaat, kimya ve biyomedikal gibi mühendislik dallarının yanı sıra jeofizik, okyanus bilimi, meteoroloji, astrofizik ve biyoloji gibi farklı birçok disiplinde kullanılır.

Türbülans veya Çalkantı bir akışkanın hareket hâlindeki düzensizliğidir. Akışkanlar dinamiğinde, türbülans veya türbülanslı akış, basınç ve akış hızında meydana gelen kaotik, stokastik değişimlerle tanımlanan bir akış rejimidir. Akışkanın düzenli katmanlar hâlinde aktığı laminer akışın aksine türbülanslı akışlar düzensiz biçimde karışarak hareket eder. Akışın hangi rejimde olduğu atalet kuvvetlerinin viskozite kuvvetlerine oranını belirten boyutsuz Reynolds sayısı ile tahmin edilebilir. Örneğin, tipik bir boru akışı için Reynolds sayısı yaklaşık 2300'ü aştıktan sonra genellikle akış, türbülanslı rejime geçer. Yüksek Reynolds sayıları türbülanslı rejimin habercisi olarak sayılabilirse de bu geçişin gerçekleştiği Reynolds sayısı birçok faktöre bağlıdır ve farklı problemlerde çok daha yüksek veya düşük bir Reynolds sayısında türbülanslı rejime geçiş olabilir.

Viskozite, akmazlık veya ağdalık, akışkanlığa karşı direnç. Viskozite, bir akışkanın, yüzey gerilimi altında deforme olmaya karşı gösterdiği direncin ölçüsüdür. Akışkanın akmaya karşı gösterdiği iç direnç olarak da tanımlanabilir. Viskozitesi yüksek olan sıvılar ağdalı olarak tanımlanırlar.

Akışkanlar dinamiği alanında, Reynolds sayısı, farklı durumlarda akışkan akışı desenlerini tahmin etmeye yardımcı olan bir boyutsuz sayıdır ve eylemsizlik kuvvetleri ile viskoz kuvvetler arasındaki oranı ölçer. Düşük Reynolds sayılarında, akışlar genellikle laminer akış tarafından domine edilirken, yüksek Reynolds sayılarında akışlar genellikle türbülanslı olur. Türbülans, akışkanın hız ve yönündeki farklılıklardan kaynaklanır ve bazen bu yönler kesişebilir veya akışın genel yönüne ters hareket edebilir. Bu girdap akımları, akışı karıştırmaya başlar ve bu süreçte enerji tüketir, bu da sıvılarda kavitasyon olasılığını artırır.
Prandtl sayısı  boyutsuz bir sayıdır. Momentum yayınımının termal yayınıma oranıdır. Sayı, Alman fizikçi Ludwig Prandtl'a ithafen adlandırılmıştır.
boyutsuz bir sayıdır. Momentum yayınımının termal yayınıma oranıdır. Sayı, Alman fizikçi Ludwig Prandtl'a ithafen adlandırılmıştır.

Dean akışı, eğrisel kanallarda eğrilikten kaynaklanan bir akıştır. Dean akışı, Dean sayısının büyümesi ile etkisini gösterir. Dean sayısı boyutsuz bir sayıdır. İngiliz araştırmacı William Reginald Dean kanal içindeki akış için Dean sayısını:
Stokes Akışı George Gabriel Stokes tarafından geliştirilmiştir. Aynı zamanda sürünme akışı olarak da adlandırılır. Bu akışlar, advektif Atalet kuvvetlerinin viskoz kuvvetlere göre küçük olduğu akışlardır. Adveksiyon, herhangi bir dinamik davranışta korunan değerlerin parçacıklar veya sistemler arasındaki kütlesel hareket ile taşınımıdır. Atalet kuvvetlerinin küçük olması ise hareketlerin düşük hızlı olduğunu ifade eder. Bunlara bağlı olarak Stokes Akışları Reynolds Sayısının küçük olduğu akışlardaki basitleştirilmiş modeldir. Bu tipik durumun olduğu akışlarda hız oldukça yavaştır ve viskozite çok yüksektir veya karakteristik uzunlukların oranı küçüktür. Sürünme akışı ilk olarak göreceli hareketin küçük olduğu veya statik olan mekanik parçaların yağlanmasında incelenmiştir. Ayrıca bu akış doğada mikroorganizmaların akışkanlar içindeki hareketlerinde gözlenir. Teknolojide ise MEMS’de ve polimerlerde bu akış görülebilir.
Termodinamik ve akışkanlar mekaniği gibi bilim dallarında kullanım alanı bulan iki çeşit Bejan sayısı (Be) bulunmaktadır. Bu sayılar, Adrian Bejan'ın adını taşımaktadır.
Brinkman sayısı (Br), bir duvardan akan viskoz bir akışkana ısı iletimiyle ilişkili boyutsuz bir büyüklüktür ve genellikle polimer işleme alanında kullanılmaktadır. Bu sayı, Hollandalı matematikçi ve fizikçi Henri Brinkman'a ithafen adlandırılmıştır. Birden fazla tanım bulunmaktadır; bunlardan biri şöyledir:
Cauchy sayısı (Ca), süreklilik mekaniği alanında, özellikle sıkıştırılabilir akışların çalışılmasında kullanılan boyutsuz bir niceliktir. Bu sayı, Fransız matematikçi Augustin Louis Cauchy'ye atfen adlandırılmıştır. Sıkıştırılabilirliğin önemli olduğu durumlarda, dinamik benzerlik sağlamak için elastik kuvvetler, atalet kuvvetleriyle birlikte göz önünde bulundurulmalıdır. Bu bağlamda, Cauchy sayısı, bir akış içerisindeki atalet kuvvetleri ile sıkıştırılabilirlik kuvveti arasındaki oran olarak tanımlanmakta ve şu formülle ifade edilmektedir:
 ,
,
Euler sayısı (Eu), akışkan akışı hesaplamalarında kullanılan bir boyutsuz sayıdır. Bu sayı, yerel bir basınç düşüşü ile akışın birim hacim başına kinetik enerjisi arasındaki ilişkiyi ifade eder ve akıştaki enerji kayıplarını karakterize etmek için kullanılır. Mükemmel sürtünmesiz bir akış, Euler sayısının 0 olduğu duruma karşılık gelir. Euler sayısının tersi, sembolü Ru olan Ruark Sayısı olarak adlandırılır.
Akışkanlar dinamiğinde, Galilei sayısı (Ga), bazen Galileo sayısı olarak da anılır, İtalyan bilim insanı Galileo Galilei (1564-1642) adına adlandırılmış bir boyutsuz sayıdır.

Akışkanlar dinamiği alanında, Keulegan–Carpenter sayısı, aynı zamanda periyot sayısı olarak da bilinir, salınımlı bir akışkan akışı içinde bulunan künt cisimler üzerindeki sürükleme kuvvetinin atalet kuvvetlerine göre göreli önemini belirten bir boyutsuz niceliktir. Aynı şekilde, durgun bir akışkan içinde salınan cisimler için de geçerlidir. Küçük Keulegan–Carpenter sayılarında atalet kuvvetleri baskınken, büyük sayılarda türbülans nedeniyle sürükleme kuvvetleri önem kazanır.

Akışkanlar dinamiği alanında, sürükleme katsayısı, bir nesnenin hava veya su gibi bir akışkan ortamında maruz kaldığı sürükleme veya direnç miktarını belirlemek için kullanılan bir boyutsuz niceliktir. Sürükleme denkleminde kullanılır ve daha düşük bir sürükleme katsayısı, nesnenin daha az aerodinamik veya hidrodinamik sürüklemeye sahip olacağını ifade eder. Sürükleme katsayısı her zaman belirli bir yüzey alanına bağlı olarak değerlendirilir.
Laplace sayısı (La), diğer adıyla Suratman sayısı (Su), serbest yüzey akışkanlar dinamiği karakterizasyonunda kullanılan bir boyutsuz sayıdır. Bu sayı, yüzey gerilimi ile akışkan içindeki momentum taşınımı arasındaki oranı temsil eder.
Akışkanlar dinamiğinde, bir akışkanın Schmidt sayısı, momentum difüzivitesi ile kütle difüzyonu oranı olarak tanımlanan bir boyutsuz sayıdır ve eşzamanlı momentum ve kütle difüzyonu konveksiyon süreçlerinin gerçekleştiği akışkan akışlarını karakterize etmek amacıyla kullanılır. Bu sayı, Alman mühendis Ernst Heinrich Wilhelm Schmidt (1892–1975) adına ithaf edilmiştir.
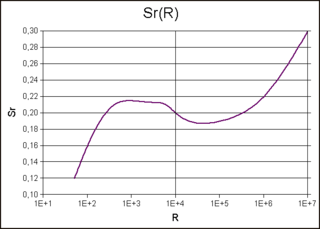
Boyut analizinde, Strouhal sayısı salınımlı akış mekanizmalarını tanımlayan bir boyutsuz sayıdır. Bu parametre, 1878 yılında vorteks saçıntısı oluşturan tellerle ve rüzgarda ses çıkaran tellerle deney yapan Çek fizikçi Vincenc Strouhal'ın adını taşır. Strouhal sayısı, akışkanlar mekaniğinin temel ilkelerinin önemli bir bileşenidir.
Akışkanlar dinamiğinde, Taylor sayısı (Ta), bir akışkanın bir eksen etrafında dönmesine bağlı olarak ortaya çıkan merkezkaç "kuvvetlerin" veya sözde atalet kuvvetlerinin viskoz kuvvetlere göre önemini karakterize eden bir boyutsuz niceliktir.
Womersley sayısı, biyoakışkan mekaniği ve biyoakışkan dinamiği alanlarında kullanılan bir boyutsuz sayıdır. Bu sayı, pulsatil akış frekansının viskoz etkilerle olan ilişkisini boyutsuz bir biçimde ifade eder. John R. Womersley (1907–1958)'in arterlerdeki kan akışı üzerine yaptığı çalışmalar nedeniyle bu adla anılmaktadır. Womersley sayısı, bir deneyin ölçeklendirilmesinde dinamik benzerlik sağlamak açısından önem taşır. Örneğin, deneysel çalışmalarda damar sisteminin ölçeklendirilmesi bu duruma örnek teşkil eder. Ayrıca, Womersley sayısı, giriş etkilerinin ihmal edilip edilemeyeceğini belirlemek için sınır tabakası kalınlığının tespitinde de önemlidir.














