İçeriğe atla

Kenar kapsama problemi

Köşe Örtme (İngilizce: Vertex Cover), bir çizge (graf) içerisindeki tüm kenarların en az sayıda seçilebilecek düğüm ile kapsanabilir olup olmadığının bulunması problemidir. Bu problemin NP sınıfı içerisinde olduğu bilinmektedir. Amaç, bu problemin NP-Tam sınıfında olup olmadığının ispatıdır.

Köşe Örtme probleminin NP sınıfı içerisinde olduğu zaten görülmektedir. Çünkü NP sınıfındaki bir probleme ilişkin verilen bir çözümün polinom zamanda doğru olup olmadığını tespit etmek mümkündür. Örneğin verilen bir grafın içinde tüm kenarları kapsayan bir alt küme olduğunu iddia eden bir çözümün doğruluğu için O(n2) zaman yeterlidir. Bu çözüm için iç içe iki tane döngü içerisinde düğümler arasındaki ilişkiyi izlemek yeterlidir.

Tanım

Köşe Örtme={(G,k)| G, k tane düğümlü bir köşe örtme alt kümesine sahip bir graftır.}} Buna göre; birer köşe örtme alt kümesine sahip olan graflardır.

köşe örtme Probleminin NP-Tam İçinde Yer Aldığının İspatı

Bir problemin NP-Tam olduğunu ispat etmek için, daha önce NP-Tam olduğu bilinen bir problemin bu probleme polinom zamanda indirgeniyor olduğunu ispat etmek yeterlidir.

Bunun için 3SAT probleminin NP-Tam olduğunun bilinmesinden yola çıkarak 3SAT <p köşe örtme (Vertex Cover) ispat edilmesi halinde köşe örtme probleminin de NP-Tam olduğu ispatlanmış olur.

Bunun için öncelikle 3SAT probleminin her bir şart cümleciğinin k tane terim ile gösteriliyor olduğunu bilmek gerekmektedir. Örneğin;

f=(x1 OR x1 OR x2)AND(!x1 OR !x2 OR !x2)AND(!x1 OR x2 OR x2)

şeklinde verilmiş 3SAT problemine uygun bir formülü graf şekline çevirmek gerekmektedir. Böylece bir 3SAT problemi graf haline çevrilmiş olur. Yukarıda verilmiş formülün graf haline çevrilmesi esnasında şu yol izlenmektedir.

Önce şart cümlecikleri içinde geçen terimler ile o terimlerin "DEĞİL" leri arasında bir kenar oluşturacak şekilde graf çizilmeye başlanır. Daha sonra şart cümleciklerini de grafa ekleyerek aynı terimleri birbirine bağlayarak graf oluşturulur. Buna göre m terim sayısı, l şart cümleciği sayısı olarak düşünülürse, 2m+3l tane düğümden oluşan bir graf ortaya çıkar. Verilen grafın içinden tüm köşeleri örtme bir düğüm alt kümesinin eleman sayısını da m+2l olarak farzedelim.

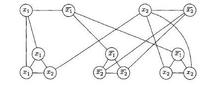
Buradaki örnekte k=8 olarak bulunur.

Bundan sonraki adım ise, köşe örtme algoritmasını gerçekleyecek ve bu koşulları olumlu olarak mantıksal doğrulanabilir sağlayacak bir karşılanabilirlik ifadesi çıkarılır. Bunun için önce grafta terimlere "doğru" karşılık gelecek kısımları seçilir. Daha sonra bu seçimin ardından, şart cümleciklerinin içinden öylesine ikişer tane düğüm seçilir ki, hem grafın kenarlarının tamamı kapsanabilir olur hem de formülde verilen şart cümleciklerinin her birisi mantıksal doğrulanabilir olur. Bunun için eğer; x1 "YANLIŞ", x2 "DOĞRU" seçilirse, o zaman yukarıdaki terimlerden !x1 ve x2 seçilip aşağıdaki şart cümleciklerinden de taralı kısımların seçilmesiyle, graftaki tüm köşe örtme olmasının yanı sıra, x1 ve x2 değerlerinin şart cümlecikleri içerisinde yerine konulmasıyla da şart cümleciklerinin her birinin mantıksal doğrulanaiblir olduğu görülür. Tüm bu işlemlerin yapılması polinom zamanda gerçeklenebildiğinden, 3SAT problemini polinom zamanda köşe örtme problemi haline dönüşebildiğinden köşe örtme problemi de NP-Tam sınıfındadır.

(x1 OR x1 OR x2)=(YANLIŞ OR YANLIŞ OR DOĞRU) =DOĞRU

(!x1 OR !x2 OR !x2)=(DOĞRU OR YANLIŞ OR YANLIŞ)=DOĞRU

(!x1 OR x2 OR x2)=(DOĞRU OR DOĞRU OR DOĞRU)=DOĞRU

Böylece yukarıdaki tüm şart cümlecikleri mantıksal doğrulanabilir olmasının yanı sıra, graf üzerinde 8 tane düğümün seçilerek tüm

köşeleri örten bir alt küme bulunmuş olur.

Buna göre oluşan grafın son hali aşağıdaki şekilde gösterildiği gibi olmaktadır.

Kaynakça

İlgili Araştırma Makaleleri

Matematiksel mantık, biçimsel mantığın matematiğe uygulanmasıyla ilgilenen bir matematik dalıdır. Metamatematik, matematiğin temelleri ve kuramsal bilgisayar bilimi alanlarıyla yakınlık gösterir. Matematiksel mantığın temel konuları biçimsel sistemlerin ifade gücünün ve biçimsel ispat sistemlerinin tümdengelim gücünün belirlenmesidir.

<span class="mw-page-title-main">Öklid geometrisi</span> Öklide atfedilen matematiksel-geometrik sistem

Öklid geometrisi, İskenderiyeli Yunan matematikçi Öklid’e atfedilen matematiksel bir sistemdir ve onun Elemanlar adlı geometri üzerine ders kitabında tarif edilmektedir. Öklid'in yöntemi, sezgisel olarak çekici küçük bir aksiyom seti varsaymaktan ve bu aksiyomlara dayanarak birçok başka önermeyi (teoremleri) çıkarmaktan ibarettir. Öklid'in sonuçlarının çoğu daha önceki matematikçiler tarafından ifade edilmiş olsa da, Öklid, bu önermelerin kapsamlı bir tümdengelimli ve mantıksal sisteme nasıl uyabileceğini gösteren ilk kişi oldu. Elemanlar, ilk aksiyomatik sistem ve resmi ispatın ilk örnekleri olarak ortaokulda (lise) hala öğretilen düzlem geometrisi ile başlar. Üç boyutlu katı geometrisi ile devam ediyor. Elemanlar’ın çoğu, geometrik dilde açıklanan, şimdi cebir ve sayı teorisi olarak adlandırılan şeyin sonuçlarını belirtir.

<span class="mw-page-title-main">NP (karmaşıklık)</span>

Nen karar problemlerini içeren karmaşıklık sınıfıdır.

<span class="mw-page-title-main">Binom dağılımı</span>

Olasılık kuramı ve istatistik bilim kollarında, binom dağılımı n sayıda iki kategori (yani başarı/başarısızlık, evet / hayır, 1/0 vb) sonucu veren denemelere uygulanır. Araştırıcının ilgi gösterdiği kategori başarı olarak adlandırılır. Bu türlü her bir deneyde, bağımsız olarak, başarı (=evet=1) olasılığının p olduğu (ve yalnızca iki kategori sonuç mümkün olduğu için başarısızlık olasılığının 1 - p olduğu) bilinir. Bu türlü bağımsız n sayıda denemeler serisi içinde elde edilen başarı sayısının ayrık olasılık dağılımı binom dağılım olarak tanımlanır. Bir binom dağılım sadece iki parametre ile, yani n ve p ile tam olarak tanımlanır. Matematik notasyon olarak bir rassal değişken X binom dağılım gösterirse şöyle ifade edilir:

X ~ B(n,p)

Matematik biliminde, özellikle yöneylem araştırması uygulamalı dalında, doğrusal programlama problemleri bir doğrusal amaç fonksiyonunun doğrusal eşitlik ve/veya eşitsizlik kısıtlamalarını sağlayacak şekilde optimizasyon yapılmasıdır. Bir optimizasyon modeli eğer sürekli değişkenlere ve tek bir doğrusal amaç fonksiyonuna sahipse ve tüm kısıtlamaları doğrusal eşitlik veya eşitsizliklerden oluşuyorsa, doğrusal (lineer) program olarak adlandırılır. Başka bir deyişle, modelin tek-amaçlı fonksiyonu ve tüm kısıtlamaları, süreklilik gösteren karar değişkenlerinin ağırlıklı toplamlarından oluşmalıdır.

SAT problemi bir NP-tam sınıfı problemidir.

Hamilton Yolu, yönlü veya yönsüz bir grafta Hamilton yolu veya Hamilton devresinin olup olmadığının kararının verilmesinin problemidir.

3SAT ve KLIK problemleri, Turing makinasından polinom zamanda kararlaştırılabilen NP problemleri arasında yer alır. Bu problemlerin birbirinin cinsine çevrilmesine indirgeme denilir.

Bilgisayar bilimlerinde, alt küme toplamı problemi karmaşıklık kuramında ve kriptografide önemli yeri olan bir problemdir.

<span class="mw-page-title-main">Argüman</span> ikna etmeye çalışmak ya da sabitleştirmek veya gerçek bir sonuca varmak

Mantık ve felsefede argüman; sonuç ve onun doğruluk derecesini belirlemeye yönelik verilen öncüllerden kurulmuş bir dizi ifadedir. Bir argüman ifadelerden oluşur. Bunlardan biri sonuç, diğerleri sonucun doğruluğuna dayanak olarak verilen öncüllerdir. Herhangi bir düşünceyle karşılaştığımızda, o düşüncenin içerdiği esas iddiayı ileten ifade argümanın sonucu; onu destekleyen diğer tüm ifadeler argümanın öncülleridir. Bir argümanın doğal dildeki mantıksal formu, sembolik biçimsel dilde temsil edilebilir ve doğal dilden bağımsız şekilde, matematik ve bilgisayar bilimlerinde biçimsel olarak tanımlanmış argümanlar yapılabilir.

<span class="mw-page-title-main">Pergel ve çizgilik çizimleri</span>

Pergel ve çizgilik çizimi, belli uzunlukta doğrular, belli büyüklükte açılar ve diğer geometrik şekilleri çizmek için sadece ideal bir çizgilik ve pergel kullanılmasıdır.

Sayı teorisinde, asal çarpanlara ayırma bir bileşik sayının, çarpıldıklarında yine aynı sayıyı verecek şekilde, bir ve kendisi dışındaki bölenlerine ayrılmasıdır.

Hamilton yolu problemi, Hamilton yolunun çözümü ile ilgili problemdir.

Bilimsel kuram; iyi kanıtlanmış, sürekli olarak test edilen ve doğrulanan deney ve gözlem ile bilimsel metot aracılığıyla elde edilen, doğanın bazı yönlerinin açıklamasıdır. Tüm bilimsel bilgiler gibi, bilimsel kuramlar doğaları gereği tümevarımsaldır, tahmin edilebilir gücü ve açıklayıcı kuvveti amaçlar. Bilimsel bir kuramın gücü, açıklayabildiği durumların çeşitliliği, anlaşılabilirliği ve kolaylığı ile ilişkilidir. Yeni bilimsel kanıtlar elde edildikçe, yeni bulgulara uymaması durumda, bilimsel bir kuram reddedilebilir ya da değiştirilebilir. Böyle durumlarda, daha doğru bir kuram benimsenir. Bazı durumlarda, doğruluğu kesin olmayan, değiştirilmemiş bir bilimsel kuram, özel bazı durumlara benzerliği açısından kullanışlı ise yine de kuram olarak ele alınır. Bilimsel kuramlar test edilebilir ve yanlış/çürütülebilir tahminler üretebilirler. Bilimsel kuramlar doğal olaylardan sorumlu bazı nedensel elementleri açıklarlar ve fiziksel evrenin yönleri ile elektrik, kimya, astronomi gibi özel araştırma alanlarını tahmin etmek ve açıklamak için kullanılırlar. Bilim insanları kuramları, teknolojiyi geliştirmek ve hastalıklara çare bulmak gibi amaçlar dışında, daha sonraki bilimsel bilgiler için temel olarak da kullanırlar. Bilimsel kuramlar, bilimsel bilginin en güvenilir, en kesin ve kapsamlı formudur. Bu, varsayım, hipotez ya da tahmin anlamlarına gelebilen kuram kelimesinin genel kullanımından büyük ölçüde farklıdır.

Tarih boyunca matematiğin konu çeşitliliği ve derinliği artmaktadır, matematiği kavrama, birçok konuyu matematiğin daha genel alanlarına göre sınıflandırma ve düzenleme için bir sistem gerektirir. Bir dizi farklı sınıflandırma şeması ortaya çıkmıştır ve bazı benzerlikleri paylaşsalar da, kısmen hizmet ettikleri farklı amaçlara bağlı olarak farklılıkları vardır. Ek olarak, matematik geliştirilmeye devam ettikçe, bu sınıflandırma şemaları da yeni oluşturulan alanları veya farklı alanlar arasında yeni keşfedilen bağlantıları dikkate alacak şekilde değişmelidir. Farklı alanlar arasındaki sınırı aşan, genellikle en aktif olan bazı konuların sınıflandırılması daha zor hale gelir.

Rönesans'tan bu yana, her yüzyılda, bir önceki göre daha fazla matematik problemi çözülmüştür. Yine de birçok büyük ve küçük problem çözüme kavuşturulamamıştır. Uzun süredir var olan bir sorunun çözümü için genellikle ödüller verilir ve çözülmemiş sorunların listeleri büyük önem kazanır. Çözülmemiş problemler, aralarında fizik, bilgisayar bilimi, cebir, matematiksel analiz, Kombinatorik, cebirsel geometri, ayrık geometri, Öklid geometrisi, katma ve cebirsel geometri teorileri, çizge teorisi, grup kuramı, modeller kuramı, sayılar teorisi, kümeler kuramı, Ramsey Kuramı, dinamik sistemler, Kısmi diferansiyel denklemler gibi birçok alanda varlığını sürdürmektedir.

<span class="mw-page-title-main">Geometri tarihi</span> Geometrinin tarihsel gelişimi

Geometri, mekansal ilişkilerle ilgilenen bilgi alanı olarak ortaya çıkmıştır. Geometri, modern öncesi matematiğin iki alanından biriydi, diğeri ise sayıların incelenmesi yani aritmetikti.

<span class="mw-page-title-main">Bézout teoremi</span> aciklama

Bézout teoremi, cebirsel geometride n değişkenli n polinomun ortak sıfırlarının sayısı ile ilgili bir ifadedir. Orijinal biçiminde teorem, genel olarak ortak sıfırların sayısının, polinomların derecelerinin çarpımına eşit olduğunu belirtir. Adını Fransız matematikçi Étienne Bézout'dan almıştır.

<span class="mw-page-title-main">Matematikte simetri</span> matematikte simetri kavramı

Simetri yalnızca geometride değil, matematiğin diğer dallarında da ortaya çıkar. Simetri bir tür değişmezliktir: matematiksel bir nesnenin bir dizi işlem veya dönüşüm altında değişmeden kaldığı özelliktir.


Bu sayfa, bu Vikipedi makalesine dayanmaktadır.
Metin, CC BY-SA 4.0 lisansı altında mevcuttur; ek koşullar uygulanabilir.
Görseller, videolar ve sesler kendi lisansları altında mevcuttur.