Kavitasyon sayısı

Kavitasyon sayısı olarak adlandırılabilecek üç boyutsuz sayı mevcuttur: hidrodinamik kavitasyon durumları için kavitasyon sayısı, pompalarda kavitasyon için Thoma sayısı ve ultrasonik kavitasyon için Garcia-Atance sayısı.

Kavitasyon sayısı (Ca), hidrodinamik kavitasyonun tahmin edilmesinde kullanılabilir. Bu sayı, yapısal olarak Euler sayısına benzerlik göstermekle birlikte farklı bir anlam ve kullanıma sahiptir:

Kavitasyon sayısı, bir akışkanın yerel mutlak basıncının buhar basıncından olan farkı ile hacim başına düşen kinetik enerji arasındaki ilişkiyi temsil eder ve bu, akışın kavitasyon oluşturma potansiyelini değerlendirmede kullanılır.

Aşağıdaki şekilde tanımlanmıştır:^[1]

${\displaystyle \mathrm {Ca} ={\frac {p-p_{\mathrm {v} }}{{\frac {1}{2}}\rho v^{2}}}}$

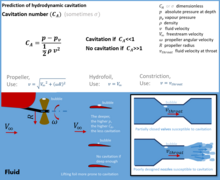
burada

• ${\displaystyle \rho }$, akışkanın yoğunluğunu,
• ${\displaystyle p}$, yerel basıncı,
• ${\displaystyle p_{\mathrm {v} }}$, akışkanın buhar basıncını,
• ${\displaystyle v}$, akışın karakteristik hızını ifade eder.

Kavitasyon sayısı, bir sıvı sistem içerisinde kavitasyon oluşumunu değerlendirmek için kullanılan temel metodlardan biridir. Kavitasyon sayısının düşük olması yüksek kavitasyon olasılığını, yüksek olması ise kavitasyonun olmadığını gösterir.

Bir sıvı kanalı, boru ya da kısıtlama içinde, yukarı yönde basınç artışı ile birlikte çalışma akışkanının hızı da artar. Ancak, hızın karesinin artış hızının, basınç artışını büyük ölçüde aşması dikkate değerdir. Bu durum, kavitasyon sayısının, yukarı yönde basınç arttıkça düşme eğilimi gösterdiği ve sistemde kavitasyon riskinin arttığı durumlara işaret eder.

Kavitasyonun başlaması, sistem içerisinde kavitasyon kabarcıklarının ilk kez oluşması ile gerçekleşir ve bu durum, başlangıç kavitasyon sayısını belirler. Bu değer, kavitasyon varlığında sistemde tespit edilen en yüksek kavitasyon sayısını ifade eder. Araştırmacılar, bu fenomenin zarar vermeyen uygulamalarını incelediklerinde, özellikle düşük yukarı akış basınçlarında kavitasyonun ilk oluşumunu belgelemeyi amaçlar.

Kavitasyon akışının evrimi sürecinde, kavitasyon sayısı giderek azalır ve sistem süperkavitasyon durumuna ulaşır; bu aşama, en yüksek ulaşılabilir hız ve akış oranı ile tanımlanır. Daha düşük kavitasyon sayıları, daha şiddetli bir kavitasyon akışının göstergesidir.

Süperkavitasyon sonrasında, sistem yukarı akış basıncı artmaya devam ettiği halde, sıvı yönetim kapasitesinin sınırlarına ulaşır. Bu durum sonucunda, ölçülen kavitasyon sayısı artış gösterir. Bu eğilim, alan literatüründe pek çok yayında tekrar eden bir bulgu olarak karşımıza çıkar.^[2]

Thoma sayısı (${\displaystyle \sigma }$), bir pompanın emiş kısmında kavitasyonun öngörülmesi için kullanılabilecek boyutsuz bir ölçüttür. Bu sayı, aşağıdaki formül ile tanımlanır:^[3]

${\displaystyle \mathrm {\sigma } ={\frac {NPSH}{h_{\mathrm {pump} }}}}$

Burada ${\displaystyle NPSH}$, net pozitif emme yükünü ifade eder ve ${\displaystyle h_{\mathrm {pump} }}$, pompanın ürettiği hidrolik düşü belirtir. Eğer Thoma sayısı, kritik kavitasyon parametresinden veya tanımlanmış kritik Thoma sayısından daha düşükse, pompanın emme kısmında kavitasyon meydana gelir:

${\displaystyle \mathrm {\sigma _{\mathrm {c} }} ={\frac {NPSHR}{h_{\mathrm {pump} }}}}$

Bu durumda, ${\displaystyle NPSHR}$, kavitasyonun önlenmesi için gereken net pozitif emme yükünü temsil eder ve bu değer her pompa modeli için deneysel olarak belirlenir.

• Euler sayısı, bir akış içerisindeki kısıtlamadan kaynaklanan yerel basınç düşüşünü tanımlamak amacıyla kullanılan bir ölçüttür ve bu sayı, kavitasyon sayısına benzer bir yapıda değerlendirilir.